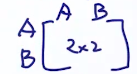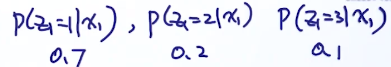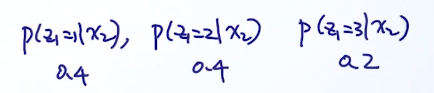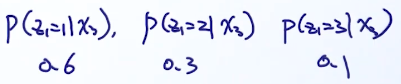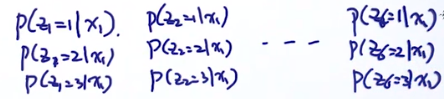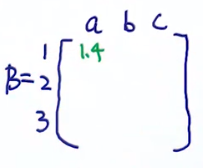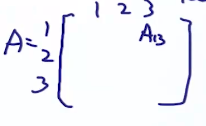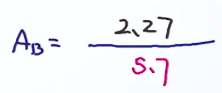公式输入请参考:
在线Latex公式
不能免俗,讲下丢硬币的例子,现在有两个硬币A和B,它们出现正面的概率分别是
μ
1
,
μ
2
\mu_1,\mu_2
μ 1 , μ 2
μ
1
,
μ
2
\mu_1,\mu_2
μ 1 , μ 2
问题一:维特比解决
隐变量
z
i
z_i
z i
x
i
x_i
x i
θ
=
(
A
,
B
,
π
)
\theta=(A,B,\pi)
θ = ( A , B , π )
A
A
A
A
i
j
A_{ij}
A i j
z
i
z_i
z i
z
j
z_j
z j
B
B
B
z
i
z_i
z i
x
i
x_i
x i
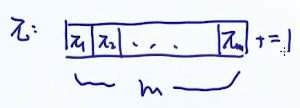
π
=
[
π
1
,
π
2
,
.
.
.
,
π
m
]
,
π
1
+
π
2
+
.
.
.
+
π
m
=
1
\pi=[\pi_1,\pi_2,...,\pi_m],\pi_1+\pi_2+...+\pi_m=1
π = [ π 1 , π 2 , . . . , π m ] , π 1 + π 2 + . . . + π m = 1
θ
,
x
\theta,x
θ , x
z
z
z
x
x
x
θ
\theta
θ
最笨的方法,适合用于隐变量状态较少的情况,把所有可能生出观察变量的排列组合全部列举出来,然后计算似然概率,取最大值。
三个可能性,序列长度是10,那么可能性就是
3
10
3^{10}
3 1 0
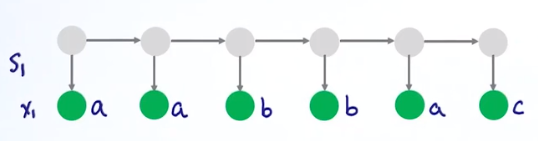
使用维特比算法的一个前提是,某个状态只和它前后的状态有关,与其他状态无关。
z
i
z_i
z i
1
∼
m
1\sim m
1 ∼ m
θ
,
x
\theta,x
θ , x
z
i
z_i
z i
z
1
z_1
z 1
1
∼
m
1\sim m
1 ∼ m
z
2
z_2
z 2
1
∼
m
1\sim m
1 ∼ m
z
1
z_1
z 1
p
(
z
1
=
2
)
p(z_1=2)
p ( z 1 = 2 )
π
\pi
π
z
1
=
2
z_1=2
z 1 = 2
x
1
x_1
x 1
p
(
z
1
=
2
)
p
(
x
1
∣
z
1
=
2
)
p(z_1=2)p(x_1|z_1=2)
p ( z 1 = 2 ) p ( x 1 ∣ z 1 = 2 )
z
2
z_2
z 2
z
1
=
2
z_1=2
z 1 = 2
p
(
z
2
=
1
∣
z
1
=
2
)
p
(
x
2
∣
z
2
=
1
)
p(z_2=1|z_1=2)p(x_2|z_2=1)
p ( z 2 = 1 ∣ z 1 = 2 ) p ( x 2 ∣ z 2 = 1 )
p
(
z
1
=
2
)
p
(
x
1
∣
z
1
=
2
)
p
(
z
2
=
1
∣
z
1
=
2
)
p
(
x
2
∣
z
2
=
1
)
.
.
.
p(z_1=2)p(x_1|z_1=2)p(z_2=1|z_1=2)p(x_2|z_2=1)...
p ( z 1 = 2 ) p ( x 1 ∣ z 1 = 2 ) p ( z 2 = 1 ∣ z 1 = 2 ) p ( x 2 ∣ z 2 = 1 ) . . .
k
k
k
δ
k
(
i
)
\delta_k(i)
δ k ( i )
i
i
i
k
+
1
k+1
k + 1
k
+
1
k+1
k + 1
δ
k
+
1
(
j
)
=
m
a
x
{
δ
k
(
1
)
+
l
o
g
p
(
z
k
+
1
=
j
∣
z
k
=
1
)
+
l
o
g
p
(
x
k
+
1
∣
z
k
+
1
=
j
)
δ
k
(
2
)
+
l
o
g
p
(
z
k
+
1
=
j
∣
z
k
=
2
)
+
l
o
g
p
(
x
k
+
1
∣
z
k
+
1
=
j
)
⋮
δ
k
(
m
)
+
l
o
g
p
(
z
k
+
1
=
j
∣
z
k
=
m
)
+
l
o
g
p
(
x
k
+
1
∣
z
k
+
1
=
j
)
\delta_{k+1}(j)=max\begin{cases} &\delta_k(1)+logp(z_{k+1}=j|z_k=1) +logp(x_{k+1}|z_{k+1}=j)\\ & \delta_k(2)+logp(z_{k+1}=j|z_k=2) +logp(x_{k+1}|z_{k+1}=j) \\ &\vdots\\ & \delta_k(m)+logp(z_{k+1}=j|z_k=m) +logp(x_{k+1}|z_{k+1}=j) \end{cases}
δ k + 1 ( j ) = m a x ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎧ δ k ( 1 ) + l o g p ( z k + 1 = j ∣ z k = 1 ) + l o g p ( x k + 1 ∣ z k + 1 = j ) δ k ( 2 ) + l o g p ( z k + 1 = j ∣ z k = 2 ) + l o g p ( x k + 1 ∣ z k + 1 = j ) ⋮ δ k ( m ) + l o g p ( z k + 1 = j ∣ z k = m ) + l o g p ( x k + 1 ∣ z k + 1 = j )
δ
k
+
1
(
j
)
=
m
a
x
i
[
δ
k
(
i
)
+
l
o
g
p
(
z
k
+
1
=
j
∣
z
k
=
i
)
+
l
o
g
p
(
x
k
+
1
∣
z
k
+
1
=
j
]
\delta_{k+1}(j)=\underset{i}{max}[\delta_k(i)+logp(z_{k+1}=j|z_k=i)+logp(x_{k+1}|z_{k+1}=j]
δ k + 1 ( j ) = i ma x [ δ k ( i ) + l o g p ( z k + 1 = j ∣ z k = i ) + l o g p ( x k + 1 ∣ z k + 1 = j ]
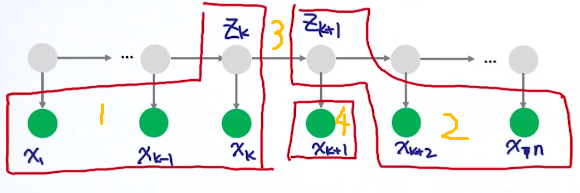
这个算法是用来估计:
p
(
z
k
∣
x
)
p(z_k|x)
p ( z k ∣ x )
p
(
z
k
,
x
1
:
k
)
p(z_k,x_{1:k})
p ( z k , x 1 : k )
p
(
x
(
k
+
1
)
:
n
∣
z
k
)
p(x_{(k+1):n}|z_k)
p ( x ( k + 1 ) : n ∣ z k )
p
(
z
k
∣
x
)
=
p
(
z
k
,
x
)
p
(
x
)
∝
p
(
z
k
,
x
)
p(z_k|x)=\cfrac{p(z_k,x)}{p(x)}\propto p(z_k,x)
p ( z k ∣ x ) = p ( x ) p ( z k , x ) ∝ p ( z k , x )
p
(
z
k
,
x
)
=
p
(
x
(
k
+
1
)
:
n
∣
z
k
,
x
1
:
k
)
p
(
z
k
,
x
1
:
k
)
p(z_k,x)=p(x_{(k+1):n}|z_k,x_{1:k})p(z_k,x_{1:k})
p ( z k , x ) = p ( x ( k + 1 ) : n ∣ z k , x 1 : k ) p ( z k , x 1 : k )
x
1
:
k
x_{1:k}
x 1 : k
x
(
k
+
1
)
:
n
x_{(k+1):n}
x ( k + 1 ) : n
z
k
z_k
z k
x
(
k
+
1
)
:
n
x_{(k+1):n}
x ( k + 1 ) : n
p
(
z
k
,
x
)
=
p
(
x
(
k
+
1
)
:
n
∣
z
k
)
p
(
z
k
,
x
1
:
k
)
p(z_k,x)=p(x_{(k+1):n}|z_k)p(z_k,x_{1:k})
p ( z k , x ) = p ( x ( k + 1 ) : n ∣ z k ) p ( z k , x 1 : k )
p
(
z
k
,
x
)
p(z_k,x)
p ( z k , x )
p
(
z
k
∣
x
)
p(z_k|x)
p ( z k ∣ x )
p
(
z
1
∣
x
)
=
p
(
z
1
,
x
)
∑
j
p
(
z
k
=
j
,
x
)
p(z_1|x)=\cfrac{p(z_1,x)}{\sum_{j}p(z_k=j,x)}
p ( z 1 ∣ x ) = ∑ j p ( z k = j , x ) p ( z 1 , x )
算法目标是求:
p
(
z
k
,
x
1
:
k
)
p(z_k,x_{1:k})
p ( z k , x 1 : k )
α
k
(
z
k
)
\alpha_k(z_k)
α k ( z k )
p
(
z
k
,
x
1
:
k
)
=
∑
z
k
−
1
p
(
z
k
−
1
,
z
k
,
x
1
:
k
)
p(z_k,x_{1:k})=\sum_{z_{k-1}}p(z_{k-1},z_k,x_{1:k})
p ( z k , x 1 : k ) = z k − 1 ∑ p ( z k − 1 , z k , x 1 : k )
z
k
−
1
z_{k-1}
z k − 1
p
(
z
k
,
x
1
:
k
)
=
∑
z
k
−
1
p
(
z
k
,
x
1
:
k
)
p
(
z
k
∣
z
k
,
x
1
:
k
)
p
(
x
k
∣
z
k
,
z
k
−
1
,
x
1
:
k
−
1
)
p(z_k,x_{1:k})=\sum_{z_{k-1}}p(z_k,x_{1:k})p(z_k|z_k,x_{1:k})p(x_k|z_k,z_{k-1},x_{1:k-1})
p ( z k , x 1 : k ) = z k − 1 ∑ p ( z k , x 1 : k ) p ( z k ∣ z k , x 1 : k ) p ( x k ∣ z k , z k − 1 , x 1 : k − 1 )
p
(
z
k
,
x
1
:
k
)
=
∑
z
k
−
1
p
(
z
k
,
x
1
:
k
)
p
(
z
k
∣
z
k
)
p
(
x
k
∣
z
k
)
p(z_k,x_{1:k})=\sum_{z_{k-1}}p(z_k,x_{1:k})p(z_k|z_k)p(x_k|z_k)
p ( z k , x 1 : k ) = z k − 1 ∑ p ( z k , x 1 : k ) p ( z k ∣ z k ) p ( x k ∣ z k )
p
(
z
1
,
x
1
)
=
p
(
z
1
)
p
(
x
1
∣
z
1
)
p(z_1,x1)=p(z_1)p(x_1|z_1)
p ( z 1 , x 1 ) = p ( z 1 ) p ( x 1 ∣ z 1 )
算法目标是求:
p
(
x
(
k
+
1
)
:
n
∣
z
k
)
p(x_{(k+1):n}|z_k)
p ( x ( k + 1 ) : n ∣ z k )
β
k
(
z
k
)
\beta_k(z_k)
β k ( z k )
p
(
x
(
k
+
1
)
:
n
∣
z
k
)
=
∑
z
k
+
1
p
(
x
(
k
+
1
)
:
n
,
z
k
+
1
∣
z
k
)
=
∑
z
k
+
1
p
(
x
(
k
+
2
)
:
n
∣
z
k
+
1
,
z
k
,
x
k
+
1
)
p
(
x
k
+
1
∣
z
k
+
1
,
z
k
)
p
(
z
k
+
1
∣
z
k
)
=
∑
z
k
+
1
p
(
x
(
k
+
2
)
:
n
∣
z
k
+
1
)
p
(
x
k
+
1
∣
z
k
+
1
)
p
(
z
k
+
1
∣
z
k
)
p(x_{(k+1):n}|z_k)=\sum_{z_{k+1}}p(x_{(k+1):n},z_{k+1}|z_k)\\ =\sum_{z_{k+1}}p(x_{(k+2):n}|z_{k+1},z_k,x_{k+1})p(x_{k+1}|z_{k+1},z_k)p(z_{k+1}|z_k)\\ =\sum_{z_{k+1}}p(x_{(k+2):n}|z_{k+1})p(x_{k+1}|z_{k+1})p(z_{k+1}|z_k)
p ( x ( k + 1 ) : n ∣ z k ) = z k + 1 ∑ p ( x ( k + 1 ) : n , z k + 1 ∣ z k ) = z k + 1 ∑ p ( x ( k + 2 ) : n ∣ z k + 1 , z k , x k + 1 ) p ( x k + 1 ∣ z k + 1 , z k ) p ( z k + 1 ∣ z k ) = z k + 1 ∑ p ( x ( k + 2 ) : n ∣ z k + 1 ) p ( x k + 1 ∣ z k + 1 ) p ( z k + 1 ∣ z k )
假定隐变量只有三个状态:1,2,3
假设隐状态有三个:1,2,3
β
k
(
i
,
j
)
\beta_k(i,j)
β k ( i , j )
p
(
z
k
=
1
,
z
k
+
1
=
1
∣
x
)
∝
β
k
(
1
,
1
)
p(z_k=1,z_{k+1}=1|x)\propto \beta_k(1,1)
p ( z k = 1 , z k + 1 = 1 ∣ x ) ∝ β k ( 1 , 1 )
p
(
z
k
=
1
,
z
k
+
1
=
2
∣
x
)
∝
β
k
(
1
,
2
)
p(z_k=1,z_{k+1}=2|x)\propto \beta_k(1,2)
p ( z k = 1 , z k + 1 = 2 ∣ x ) ∝ β k ( 1 , 2 )
p
(
z
k
=
1
,
z
k
+
1
=
3
∣
x
)
∝
β
k
(
1
,
3
)
p(z_k=1,z_{k+1}=3|x)\propto \beta_k(1,3)
p ( z k = 1 , z k + 1 = 3 ∣ x ) ∝ β k ( 1 , 3 )
p
(
z
k
=
2
,
z
k
+
1
=
1
∣
x
)
∝
β
k
(
2
,
1
)
⋮
p(z_k=2,z_{k+1}=1|x)\propto \beta_k(2,1)\\ \vdots
p ( z k = 2 , z k + 1 = 1 ∣ x ) ∝ β k ( 2 , 1 ) ⋮
p
(
z
k
=
3
,
z
k
+
1
=
3
∣
x
)
∝
β
k
(
3
,
3
)
p(z_k=3,z_{k+1}=3|x)\propto \beta_k(3,3)
p ( z k = 3 , z k + 1 = 3 ∣ x ) ∝ β k ( 3 , 3 )
p
(
z
k
=
1
,
z
k
+
1
=
1
∣
x
)
=
β
k
(
1
,
1
)
β
k
(
1
,
1
)
+
β
k
(
1
,
2
)
+
β
k
(
1
,
3
)
+
.
.
.
+
β
k
(
3
,
3
)
p(z_k=1,z_{k+1}=1|x)=\cfrac{ \beta_k(1,1)}{ \beta_k(1,1)+\beta_k(1,2)+\beta_k(1,3)+...+\beta_k(3,3)}
p ( z k = 1 , z k + 1 = 1 ∣ x ) = β k ( 1 , 1 ) + β k ( 1 , 2 ) + β k ( 1 , 3 ) + . . . + β k ( 3 , 3 ) β k ( 1 , 1 )
Complete Case:
(
z
,
x
)
(z,x)
( z , x )
(
x
)
(x)
( x )
z
z
z
π
\pi
π
值
1
2
3
出现次数
2
1
0
π取值
2/3
1/3
0
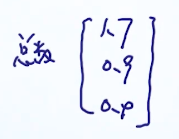
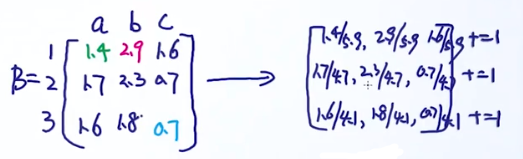
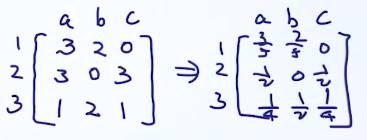
估计A,根据定义,A是3*3的矩阵,先写出状态转移次数,例如左边矩阵中的第一行第一列的数字代表从状态1转移到状态1的次数一共有2次,第一行第二列的数字代表从状态1转移到状态2的次数一共有1次,以此类推:
[
2
1
2
1
2
1
0
2
1
]
\begin{bmatrix} 2 &1 &2 \\ 1 &2 & 1\\ 0 &2 &1 \end{bmatrix}
⎣ ⎡ 2 1 0 1 2 2 2 1 1 ⎦ ⎤
[
2
/
5
1
/
5
2
/
5
1
/
4
2
/
4
1
/
4
0
2
/
3
1
/
3
]
\begin{bmatrix} 2/5 &1/5 &2/5 \\ 1/4 &2/4 &1/4\\ 0 &2/3 &1 /3 \end{bmatrix}
⎣ ⎡ 2 / 5 1 / 4 0 1 / 5 2 / 4 2 / 3 2 / 5 1 / 4 1 / 3 ⎦ ⎤
用最大似然来求解
θ
\theta
θ
l
(
θ
;
D
)
=
log
p
(
x
,
z
∣
θ
)
=
log
p
(
z
∣
θ
z
)
+
log
p
(
x
∣
z
,
θ
x
)
l(\theta;D)=\text{log}p(x,z|\theta)=\text{log}p(z|\theta_z)+\text{log}p(x|z,\theta_x)
l ( θ ; D ) = log p ( x , z ∣ θ ) = log p ( z ∣ θ z ) + log p ( x ∣ z , θ x )
l
(
θ
;
D
)
=
log
∑
z
p
(
x
,
z
∣
θ
)
=
log
∑
z
p
(
z
∣
θ
z
)
p
(
x
∣
z
,
θ
x
)
l(\theta;D)=\text{log}\sum_zp(x,z|\theta)=\text{log}\sum_zp(z|\theta_z)p(x|z,\theta_x)
l ( θ ; D ) = log z ∑ p ( x , z ∣ θ ) = log z ∑ p ( z ∣ θ z ) p ( x ∣ z , θ x )
θ
\theta
θ
x
x
x
z
z
z
L
(
θ
)
=
log
p
(
x
∣
θ
)
L(\theta)=\text{log}p(x|\theta)
L ( θ ) = log p ( x ∣ θ )
a
r
g
m
a
x
L
(
θ
)
=
a
r
g
m
a
x
log
p
(
x
∣
θ
)
argmaxL(\theta)=argmax\text{log}p(x|\theta)
a r g m a x L ( θ ) = a r g m a x log p ( x ∣ θ )
n
n
n
θ
n
\theta_n
θ n
θ
\theta
θ
θ
n
\theta_n
θ n
θ
\theta
θ
θ
n
+
1
\theta_{n+1}
θ n + 1
a
r
g
m
a
x
θ
(
L
(
θ
)
−
L
(
θ
n
)
)
=
log
p
(
x
∣
θ
)
−
log
p
(
x
∣
θ
n
)
\underset{\theta}{argmax}(L(\theta)-L(\theta_n))=\text{log}p(x|\theta)-\text{log}p(x|\theta_n)
θ a r g ma x ( L ( θ ) − L ( θ n ) ) = log p ( x ∣ θ ) − log p ( x ∣ θ n )
L
(
θ
)
−
L
(
θ
n
)
=
log
∑
z
p
(
x
,
z
∣
θ
)
−
log
p
(
x
∣
θ
n
)
=
log
∑
z
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
−
log
p
(
x
∣
θ
n
)
=
log
∑
z
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
p
(
z
∣
x
,
θ
n
)
p
(
z
∣
x
,
θ
n
)
−
log
p
(
x
∣
θ
n
)
=
log
∑
z
p
(
z
∣
x
,
θ
n
)
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
p
(
z
∣
x
,
θ
n
)
−
log
p
(
x
∣
θ
n
)
L(\theta)-L(\theta_n)=\text{log}\sum_zp(x,z|\theta)-\text{log}p(x|\theta_n)\\ =\text{log}\sum_zp(x|z,\theta)p(z|\theta)-\text{log}p(x|\theta_n)\\ =\text{log}\sum_zp(x|z,\theta)p(z|\theta)\cfrac{p(z|x,\theta_n)}{p(z|x,\theta_n)}-\text{log}p(x|\theta_n)\\ =\text{log}\sum_zp(z|x,\theta_n)\cfrac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_n)}-\text{log}p(x|\theta_n)
L ( θ ) − L ( θ n ) = log z ∑ p ( x , z ∣ θ ) − log p ( x ∣ θ n ) = log z ∑ p ( x ∣ z , θ ) p ( z ∣ θ ) − log p ( x ∣ θ n ) = log z ∑ p ( x ∣ z , θ ) p ( z ∣ θ ) p ( z ∣ x , θ n ) p ( z ∣ x , θ n ) − log p ( x ∣ θ n ) = log z ∑ p ( z ∣ x , θ n ) p ( z ∣ x , θ n ) p ( x ∣ z , θ ) p ( z ∣ θ ) − log p ( x ∣ θ n )
根据jensen’s inequality,有具体证明
∑
i
=
1
n
λ
i
=
1
\sum_{i=1}^n\lambda_i=1
∑ i = 1 n λ i = 1
log
∑
i
=
1
n
λ
i
x
i
≥
∑
i
=
1
n
λ
i
log
x
i
\text{log}\sum_{i=1}^n\lambda_ix_i\ge \sum_{i=1}^n\lambda_i\text{log}x_i
log i = 1 ∑ n λ i x i ≥ i = 1 ∑ n λ i log x i
λ
i
\lambda_i
λ i
p
(
z
∣
x
,
θ
n
)
p(z|x,\theta_n)
p ( z ∣ x , θ n )
∑
z
p
(
z
∣
x
,
θ
n
)
=
1
\sum_zp(z|x,\theta_n)=1
∑ z p ( z ∣ x , θ n ) = 1
L
(
θ
)
−
L
(
θ
n
)
≥
∑
z
p
(
z
∣
x
,
θ
n
)
log
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
p
(
z
∣
x
,
θ
n
)
−
log
p
(
x
∣
θ
n
)
L(\theta)-L(\theta_n)\ge \sum_zp(z|x,\theta_n)\text{log}\cfrac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_n)}-\text{log}p(x|\theta_n)
L ( θ ) − L ( θ n ) ≥ z ∑ p ( z ∣ x , θ n ) log p ( z ∣ x , θ n ) p ( x ∣ z , θ ) p ( z ∣ θ ) − log p ( x ∣ θ n )
log
p
(
x
∣
θ
n
)
\text{log}p(x|\theta_n)
log p ( x ∣ θ n )
log
p
(
x
∣
θ
n
)
=
1
⋅
log
p
(
x
∣
θ
n
)
=
∑
z
p
(
z
∣
x
,
θ
n
)
⋅
log
p
(
x
∣
θ
n
)
\text{log}p(x|\theta_n)=1\cdot\text{log}p(x|\theta_n)=\sum_zp(z|x,\theta_n)\cdot\text{log}p(x|\theta_n)
log p ( x ∣ θ n ) = 1 ⋅ log p ( x ∣ θ n ) = z ∑ p ( z ∣ x , θ n ) ⋅ log p ( x ∣ θ n )
L
(
θ
)
−
L
(
θ
n
)
≥
∑
z
p
(
z
∣
x
,
θ
n
)
log
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
p
(
z
∣
x
,
θ
n
)
p
(
x
∣
θ
n
)
=
Δ
(
θ
θ
n
)
L(\theta)-L(\theta_n)\ge \sum_zp(z|x,\theta_n)\text{log}\cfrac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_n)p(x|\theta_n)}=\Delta(\cfrac{\theta}{\theta_n})
L ( θ ) − L ( θ n ) ≥ z ∑ p ( z ∣ x , θ n ) log p ( z ∣ x , θ n ) p ( x ∣ θ n ) p ( x ∣ z , θ ) p ( z ∣ θ ) = Δ ( θ n θ )
L
(
θ
)
−
L
(
θ
n
)
≥
Δ
(
θ
θ
n
)
→
L
(
θ
)
≥
L
(
θ
n
)
+
Δ
(
θ
θ
n
)
L(\theta)-L(\theta_n)\ge\Delta(\cfrac{\theta}{\theta_n})\to L(\theta)\ge L(\theta_n)+\Delta(\cfrac{\theta}{\theta_n})
L ( θ ) − L ( θ n ) ≥ Δ ( θ n θ ) → L ( θ ) ≥ L ( θ n ) + Δ ( θ n θ )
L
(
θ
)
L(\theta)
L ( θ )
L
(
θ
)
L(\theta)
L ( θ )
a
r
g
m
a
x
θ
[
L
(
θ
n
)
+
Δ
(
θ
θ
n
)
]
=
a
r
g
m
a
x
θ
[
L
(
θ
n
)
+
∑
z
p
(
z
∣
x
,
θ
n
)
log
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
p
(
z
∣
x
,
θ
n
)
p
(
x
∣
θ
n
)
]
\underset{\theta}{argmax}[L(\theta_n)+\Delta(\cfrac{\theta}{\theta_n})]\\ =\underset{\theta}{argmax}[L(\theta_n)+ \sum_zp(z|x,\theta_n)\text{log}\cfrac{p(x|z,\theta)p(z|\theta)}{p(z|x,\theta_n)p(x|\theta_n)}]
θ a r g ma x [ L ( θ n ) + Δ ( θ n θ ) ] = θ a r g ma x [ L ( θ n ) + z ∑ p ( z ∣ x , θ n ) log p ( z ∣ x , θ n ) p ( x ∣ θ n ) p ( x ∣ z , θ ) p ( z ∣ θ ) ]
θ
\theta
θ
=
a
r
g
m
a
x
θ
[
∑
z
p
(
z
∣
x
,
θ
n
)
log
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
]
=
a
r
g
m
a
x
θ
[
∑
z
p
(
z
∣
x
,
θ
n
)
log
p
(
x
,
z
∣
θ
)
]
=\underset{\theta}{argmax}[ \sum_zp(z|x,\theta_n)\text{log}p(x|z,\theta)p(z|\theta)]\\ =\underset{\theta}{argmax}[ \sum_zp(z|x,\theta_n)\text{log}p(x,z|\theta)]
= θ a r g ma x [ z ∑ p ( z ∣ x , θ n ) log p ( x ∣ z , θ ) p ( z ∣ θ ) ] = θ a r g ma x [ z ∑ p ( z ∣ x , θ n ) log p ( x , z ∣ θ ) ]
根据概率公式:
p
(
A
B
)
=
p
(
A
,
B
)
=
p
(
A
∣
B
)
P
(
B
)
p(AB)=p(A,B)=p(A|B)P(B)
p ( A B ) = p ( A , B ) = p ( A ∣ B ) P ( B )
p
(
A
B
∣
C
)
=
p
(
A
,
B
∣
C
)
=
p
(
A
∣
B
,
C
)
P
(
B
∣
C
)
p(AB|C)=p(A,B|C)=p(A|B,C)P(B|C)
p ( A B ∣ C ) = p ( A , B ∣ C ) = p ( A ∣ B , C ) P ( B ∣ C )
p
(
A
,
B
∣
C
)
p(A,B|C)
p ( A , B ∣ C )
p
(
A
∣
B
,
C
)
p(A|B,C)
p ( A ∣ B , C )
p
(
x
∣
z
,
θ
)
p
(
z
∣
θ
)
=
p
(
x
,
z
∣
θ
)
p(x|z,\theta)p(z|\theta)=p(x,z|\theta)
p ( x ∣ z , θ ) p ( z ∣ θ ) = p ( x , z ∣ θ )
这里的前面一项是一个z的期望值(数学期望概念 ),所以:
=
a
r
g
m
a
x
θ
[
E
z
∣
x
,
θ
n
log
p
(
x
,
z
∣
θ
)
]
=\underset{\theta}{argmax}[E_{z|x,\theta_n}\text{log}p(x,z|\theta)]
= θ a r g ma x [ E z ∣ x , θ n log p ( x , z ∣ θ ) ]
E
z
∣
x
,
θ
n
E_{z|x,\theta_n}
E z ∣ x , θ n
log
p
(
x
,
z
∣
θ
)
\text{log}p(x,z|\theta)
log p ( x , z ∣ θ )
log
p
(
x
,
z
∣
θ
)
\text{log}p(x,z|\theta)
log p ( x , z ∣ θ )
z
z
z
E-step是求z
θ
\theta
θ
K均值本质上也是属于EM算法的一个特例。大概说一个这个算法的思想:
r
n
k
r_{nk}
r n k
r
n
k
=
1
r_{nk}=1
r n k = 1
x
n
x_n
x n
k
k
k
x
n
x_n
x n
[
0
,
0
,
.
.
.
,
1
,
.
.
.
0
]
[0,0,...,1,...0]
[ 0 , 0 , . . . , 1 , . . . 0 ]
μ
k
\mu_k
μ k
J
=
∑
n
=
1
N
∑
k
=
1
K
r
n
k
∣
∣
x
n
−
μ
k
∣
∣
2
J=\sum_{n=1}^N\sum_{k=1}^Kr_{nk}||x_n-\mu_k||^2
J = n = 1 ∑ N k = 1 ∑ K r n k ∣ ∣ x n − μ k ∣ ∣ 2
r
n
k
r_{nk}
r n k
μ
k
\mu_k
μ k
r
n
k
r_{nk}
r n k
μ
k
\mu_k
μ k
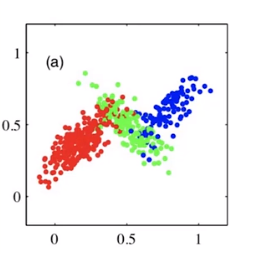
GMM在李宏毅的课里面有讲过,这里不多展开,上图。
x
x
x
z
z
z
p
(
x
,
z
=
′
r
e
d
′
)
=
N
(
x
∣
μ
1
,
Σ
1
)
p(x,z='red')=N(x|\mu_1,\Sigma_1)
p ( x , z = ′ r e d ′ ) = N ( x ∣ μ 1 , Σ 1 )
p
(
x
,
z
=
′
b
l
u
e
′
)
=
N
(
x
∣
μ
2
,
Σ
2
)
p(x,z='blue')=N(x|\mu_2,\Sigma_2)
p ( x , z = ′ b l u e ′ ) = N ( x ∣ μ 2 , Σ 2 )
p
(
x
,
z
=
′
g
r
e
e
n
′
)
=
N
(
x
∣
μ
3
,
Σ
3
)
p(x,z='green')=N(x|\mu_3,\Sigma_3)
p ( x , z = ′ g r e e n ′ ) = N ( x ∣ μ 3 , Σ 3 )
p
(
x
)
=
∑
k
=
1
K
π
k
N
(
x
∣
μ
k
,
Σ
k
)
p(x)=\sum_{k=1}^K\pi_k N(x|\mu_k,\Sigma_k)
p ( x ) = k = 1 ∑ K π k N ( x ∣ μ k , Σ k )
π
k
\pi_k
π k
μ
k
,
Σ
k
\mu_k,\Sigma_k
μ k , Σ k
log
p
(
D
∣
π
,
μ
,
Σ
)
=
∑
n
=
1
N
log
{
∑
k
=
1
K
π
k
N
(
x
∣
μ
k
,
Σ
k
)
}
\text{log}p(D|\pi,\mu,\Sigma)=\sum_{n=1}^N\text{log}\{\sum_{k=1}^K\pi_k N(x|\mu_k,\Sigma_k)\}
log p ( D ∣ π , μ , Σ ) = n = 1 ∑ N log { k = 1 ∑ K π k N ( x ∣ μ k , Σ k ) }