公式输入请参考:
在线Latex公式
起源(HMM vs CRF)
可以看到下图中横向变化,和纵向的对比(有向图和无向图)。

求有向图和无向图联合概率

有向图的联合概率等于各个节点的条件概率的乘积,当然,
x4,x5由于没有入度,所以不用条件。
注意,在计算条件概率的时候,只需要考虑局部的取值类型即可,例如:
p(x2∣x3),只用考虑
x3的取值(假设它是离散型),如果有两种值,就只用考虑两种情况。
无向图相对而言麻烦点:

这里要引入factor/feature function,这里引入这个东西就是要把上面的无向图进行拆分。拆分的结果就是上图中的绿色圈圈,三个三个一组。这样的一组也叫做clique(可以一个点做一个clique,可以两个点做一个clique,当然也可以三个做一个clique,但是必须是两两相互关联的。)拆分好后,联合概率就可以写为:
p(x1,x2,x3,x4,x5)=ϕ1(x1,x2,x3)ϕ2(x2,x3,x5)ϕ3(x3,x4,x5)
ϕ就是feature function
由于联合概率也是概率,为了保证概率的值域是[0,1],我们需要对上面的式子进行归一化,除以一个normalization term
z(x),也叫做partition function:
p(x1,x2,x3,x4,x5)=z(x)ϕ1(x1,x2,x3)ϕ2(x2,x3,x5)ϕ3(x3,x4,x5)
partition function不好求。。。因为它是依赖于全局的变量(有向图是局部依赖)。
Log-Linear Model
逻辑回归和CRF都属于Log-Linear Model的一个特例,因此我们先来看看Log-Linear Model是什么。
p(y∣x;w)=Z(x,w)exp∑j=1JwjFj(x,y)
其中:
Fj(x,y)是feature function,
wj是模型参数,
Z(x,w)是normalization term。
给出feature function的定义:
Fj(x,y)=xi⋅I(y=c)
x是d维的特征向量
y是分类,取值范围:
{1,2,...,c}。
I是indicator function,意思是当函数中的条件满足的时候函数取值为1,否则取值为0.
假设现在
c=3,那么特征函数的维度是
3×d也就是
j∈1,2,3,...,3d,同样的参数
w的维度也是
3×d
下面是不同的分类的时候,特征函数的取值情况如下:

下面来看看当分类为1的时候模型概率的计算:
p(y=1∣x;w)=Z(x,w)exp∑j=13dwjFj(x,y)=Z(x,w)exp∑j=1dwjxj
下面来看看当分类为2的时候模型概率的计算:
p(y=2∣x;w)=Z(x,w)exp∑j=13dwjFj(x,y)=Z(x,w)exp∑j=d+12dwjxj−d
注意这里的x的下标是j-d,因为x的下标范围是1-d,但是j是从d+1到2d,所以这里要减去一个d,避免数组越界。
下面来看看当分类为3的时候模型概率的计算:
p(y=3∣x;w)=Z(x,w)exp∑j=13dwjFj(x,y)=Z(x,w)exp∑j=2d+13dwjxj−2d
为了进一步展开,我们把参数写开:
w=(w1,w2,...,wd,wd+1,...,w2d,w2d+1,...,w3d)T
把它每d个分一个段,写成:
w=(w(1),w(2),w(3))T
那么,上面的分类的模型概率计算可以写为:
p(y=1∣x;w)=Z(x,w)exp(w(1)T⋅x)
p(y=2∣x;w)=Z(x,w)exp(w(2)T⋅x)
p(y=3∣x;w)=Z(x,w)exp(w(3)T⋅x)
normalization term
z(x,w)可以写成:
Z(x,w)=w(1)T⋅x+w(2)T⋅x+w(3)T⋅x
模型概率写成:
p(y=1∣x;w)=∑i=13ew(i)T⋅xew(1)T⋅x
p(y=2∣x;w)=∑i=13ew(i)T⋅xew(2)T⋅x
p(y=2∣x;w)=∑i=13ew(i)T⋅xew(3)T⋅x
以上实际上就是多元逻辑回归的形式。
feature function
上面定义的feature function是:
Fj(x,y)=xi⋅I(y=c)
实际上,我们的feature function通常可以定义为:
Fj(x,y)=Aa(x)Bb(y)
其中:
Bb(y)是标签。
Aa(x)是特征,例如:

不同的feature function得到的模型也不一样。
CRF:Log-Linear Model for Sequential Data
CRF其实就是Log-Linear Model处理时序数据的特例,因此,我们把Log-Linear Model的条件概率模型写出来,然后假设数据x是一个序列,来进行推导。原型
p(y∣x;w)=Z(x,w)1expj=1∑JwjFj(x,y)
我们假设:
xˉ是观测到的时序数据,类似一句话。
相应的有:
yˉ是观测到的时序数据对应的标签。
新的模型:
p(yˉ∣xˉ;w)=Z(x,w)1expj=1∑JwjFj(xˉ,yˉ)
由于不同的
Fj(xˉ,yˉ)可以得到不同类型的模型,因此我们先从最简单的CRF来开始推。
linear chain CRF,考虑到时序数据的特征,对特征函数做相应的定义:
p(yˉ∣xˉ;w)=Z(x,w)1expj=1∑JwjFj(xˉ,yˉ)=Z(x,w)1expj=1∑Jwji=2∑nfj(yi−1,yi,xˉ,i)
相当于把第j个特征函数看做是一个核时序有关的特征,然后把这个时序展开,并和
xˉ组成之前说过的factor
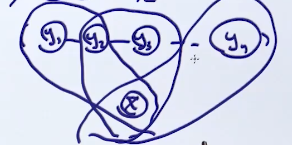
接下来看linear chain CRF两个重要问题:inference和参数估计
Inference Problem
问题描述:给定
w,xˉ,求
yˉ:
y
=argyˉmaxp(yˉ∣xˉ;w)=argyˉmaxj=1∑JwjFj(xˉ,yˉ)
这里省略掉了一部分,因为
w,xˉ可以看做常量。继续写:
y
=argyˉmaxj=1∑Jwji=2∑nfj(yi−1,yi,xˉ,i)
我们定义:
gi(yi−1,yi)=j=1∑Jwjfj(yi−1,yi,xˉ,i)
因此:
y
=i=2∑ngi(yi−1,yi)
这里借鉴上节HMM中维特比算法,求当前点的最优解,是在前一个时刻的最优解的基础上进行求极值即可:

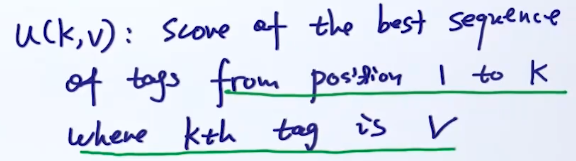
写成数学表达:
u(k,v)=y1,...,yk−1maxsumi=1k−1gi(yi−1,yi)+gk(yk−1,v)
把
yk−1单独拿出来,中括号里面就是上面的子问题。
u(k,v)=yk−1max[y1,...,yk−2maxsumi=1k−2gi(yi−1,yi)+gk−1(yk−2,yk−1)]+gk(yk−1,v)
根据函数u的定义,上面可以写成;
u(k,v)=umax[u(k−1,u)+gk(u,v)]
所以整个u就可以做是一个序列的动态规划求解:
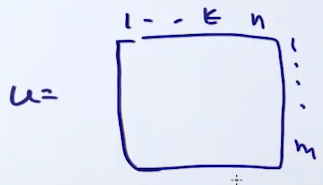
估计参数w
大概思路是第一步先看按log-linear 模型如何来求w,然后第二步再看特例CRF的w怎么求
先写出公式:
p(y∣x;w)=Z(x,w)1expj=1∑JwjFj(x,y)(1)
按梯度下降的思想来求w,实际上要计算梯度(条件概率p对
wj的偏导)
∂wj∂logp(y∣x;w)(2)
这里加一个log对求梯度没有影响,方便去掉后面e。
把公式2带入公式1:
(2)=∂wj∂logp(y∣x;w)=∂wj∂[j=1∑JwjFj(x,y)−logZ(x,w)]
然后中括号每项分别对w求导
=Fj(x,y)−Z(x,w)1⋅∂wj∂Z(x,w)(3)
之前说过,Z是一个归一化项,因此可以按类别求和后,把它写出来
Z(x,w)=y′∑expj=1∑JwjFj(x,y′)(4)
然后我们根据公式4来对
Z(x,w)求w的偏导。
∂wj∂Z(x,w)=∂wj∂y′∑expj=1∑JwjFj(x,y′)
上面的
y′与求偏导的对象无关,可以挪到前面,并且为了和前面的
j区分,这里把求和的
j写成
j′:
=y′∑∂wj∂expj′∑wj′Fj′(x,y′)=y′∑expj′∑wj′Fj′(x,y′)∂wj∂j′∑wj′Fj′(x,y′)
这里,因为
∂wj∂∑j′wj′Fj′(x,y′)求导过程中,只对第j个有结果,其他项对
wj求导都变0了,所以上面:
=y′∑[expj′∑wj′Fj′(x,y′)]Fj(x,y′)(5)
把公式5带入3:
=Fj(x,y)−Z(x,w)1y′∑[expj′∑wj′Fj′(x,y′)]Fj(x,y′)=Fj(x,y)−y′∑Fj(x,y′)Z(x,w)exp∑j′wj′Fj′(x,y′)
根据Log-Linear Model条件概率的定义最后一个分式可以写为
p(y′∣x;w),因此上式写成:
=Fj(x,y)−y′∑Fj(x,y′)p(y′∣x;w)
后面这项是考虑了
y′的各个可能,按期望的概率,可以写为:
=Fj(x,y)−y′∼p(y′∣x;w)E{Fj(x,y′)}(6)
把这个结论先记下来。
在来看如何计算
Z(xˉ,w),这个后面要用到。把它写为考虑所有的
yˉ的情况:
Z(xˉ,w)=yˉ∑expj=1∑JwjFj(xˉ,yˉ)=yˉ∑expj=1∑Jwji=2∑nfj(yi−1,yi,xˉ,i)=yˉ∑expi=2∑ngi(yi−1,yi)
要解这个,一种考虑所有的组合:
O(mn),其中n是序列的长度,m是状态个数
另外一种是用HMM里面的FB算法。
Forward algorithm:先定义
α(k+1,v)=y1,...,yk∑exp[i=2∑kgi(yi−1,yi)+gk+1(yk,v)]
意思是考虑1到k+1的子序列,前面是1到k,后面一项是k+1项,我们把这项设置为v
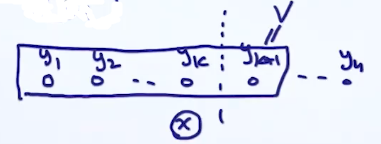
再把
yk分出来,变成
y1,...,yk−1和
yk,
yk设置为u:
α(k+1,v)=u∑y1,...,yk−1∑exp[i=2∑k−1gi(yi−1,yi)]exp[gk(yk−1,u)]exp[gk+1(u,v)]
上式中:
∑y1,...,yk−1exp[∑i=2k−1gi(yi−1,yi)]exp[gk(yk−1,u)]实际上是
α(k+1,v)的子问题。因此:
α(k+1,v)=u∑α(k,u)exp[gk+1(u,v)]
类似的,Backward algorithm可以定义:
β(u,k)=v∑[expgk+1(u,v)]β(v,k+1)
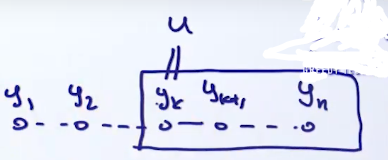
最后:
Z(xˉ,w)=u∑α(k,u)β(u,k)
这里是考虑离散型变量的序列的估计,如果是连续型,要使用蒙特卡洛方法进行估计。
有了上面的结论,我们可以很容易的计算出类似HMM某一个时刻隐变量的概率:
p(yk=u∣xˉ;w)=Z(xˉ,w)α(k,u)β(u,k)
类似的
p(yk=u,yk+1=v∣xˉ;w)=Z(xˉ,w)α(k,u)[expgk+1(u,v)]β(v,k+1)
下面可以开始解决公式6
∂wj∂logp(yˉ∣xˉ;w)=Fj(xˉ,yˉ)−y′∼p(y′∣xˉ;w)E{Fj(xˉ,y′)}=Fj(xˉ,yˉ)−yˉE[i=2∑nfj(yi−1,yi,xˉ,i)]=Fj(xˉ,yˉ)−i=2∑nyˉE[fj(yi−1,yi,xˉ,i)]
这里有个trick,期望本来是对于所有的y,也就是
yˉ,但是这里只有
yi−1,yi,所以上面可以写为:
=Fj(xˉ,yˉ)−i=2∑nyˉi−1,yiE[fj(yi−1,yi,xˉ,i)]
按期望展开:
=Fj(xˉ,yˉ)−i=2∑nyi−1∑yi∑fj(yi−1,yi,xˉ,i)⋅p(yi,yi−1∣xˉ;w)
最后:
∂wj∂logp(yˉ∣xˉ;w)=Fj(xˉ,yˉ)−i=2∑nyi−1∑yi∑fj(yi−1,yi,xˉ,i)⋅Z(xˉ,w)α(i−1,yi−1)[expgi(yi−1,yi)]β(yi,i)
有了上面的结果,我们就可以计算梯度:
wjt+1=wjt−ηt∂wj∂logp(yˉ∣xˉ;w)











