LR逻辑斯蒂回归（对数几率回归）

从LR模型的三要素出发。

模型

模型引入

       如果在线性模型 ( $z = \theta^T x$) 的基础上做分类，比如二分类任务，即 $y\in \{0,1\}$.最直观的，可以将线性模型的输出值再套上一个函数 $y = g(z)$，最简单的就是“单位阶跃函数”.
$y= \begin {cases} 0 & z<0 \\ 0.5 & z=0 \\ 1 & z>0 \end{cases}$
       预测值z大于0 的判定为类别0，小于 0 的判定为类别1，预测值为临界值可以任意判定。
       但是，这样的分段函数数学性质不太好，（形状如下图红线部分所示）它既不连续也不可微。我们知道，通常在做优化任务时，目标函数最好是连续可微的。

       这里就用到了对数几率函数 (形状如图中黑色曲线所示)：

对数几率函数（模型）

• 函数公式： $y= \frac{1}{1+e^{-z}}$
• 几率（ods）： $\frac{y}{1-y}=e^z$
• 对数几率： $ln\frac{y}{1-y}=z$
• 对数几率函数是一种“Sigmoid”函数。
• Sigmoid 函数表示形式S形的函数（形状如上图中黑色曲线所示）。

       将 $z=\theta^Tx$带入对数几率函数，得到：
$y=\frac{1}{1+e^{-\theta^Tx}}\tag{1}$
       将 $y$视为样本 $x$作为正例的可能性，则 $1-y$是其反例的可能性，根据上述几率的定义，我们可以将(1)式写为如下形式：
$ln\frac{y}{1-y}=\theta^Tx\tag{2}$
       从(2)式可以看出，我们是在用线性回归的预测结果去逼近对数几率。

       LR模型具有非常好的数学性质，其主要优势如下：

• 直接对分类可能性进行建模，无需事先假设数据分布，避免假设分布不准确带来的问题。
• 使用该函数做分类问题时，不仅可以预测出类别，还能够得到近似概率预测。这点对很多需要利用概率辅助决策的任务很有用。
• 对数几率函数是任意阶可导函数，它有着很好的数学性质，很多数值优化算法都可以直接用于求取最优解。

策略（损失函数）

       我们知道线性模型的损失函数是均方损失（MSE）：
$L=\frac{1}{n}\sum_{i=1}^{n}{(\hat{y}_i-y_i)^2}\tag{3}$
       LR模型可以用MSE吗？可以用，但是因为LR模型带入上述损失函数后，不是凸函数，所以在优化时容易陷入局部最优。
       下面我们来看LR模型的损失函数是怎么得到的？
       我们先来定义一个函数 $h_{\theta}(x)$,其作用是，对于给定的输入变量，根据选择的参数计算输出变量=1 的可能性即 $h_{\theta}(x)=p(y=1|x;\theta)$.
       例如，如果对于给定的 $x$，通过已经确定的参数计算得出 $h_{\theta}(x)=0.7$，则表示有70%的几率 $y$为正向类，相应地 $y$为负向类的几率为1-0.7=0.3。
       所以，LR模型可以重新写为如下形式：
$h_{\theta}(x)=p(y=1|x;\theta)=\frac{1}{1+e^{-\theta^Tx}}=\frac{e^{\theta^Tx}}{1+e^{\theta^Tx}}\tag{4}$
$1-h_{\theta}(x)=p(y=0|x;\theta)=\frac{1}{1+e^{\theta^Tx}}\tag{5}$
根据式(4)和式(5),可以得出：
$ln\frac{p(y=1|x)}{p(y=0|x)}={\theta^Tx}\tag{6}$
我们知道 $y$的取值为0或1，类似于二项分布，可以写成如下公式：
${p(y|x)}={p(y=1|x)^y}{(1-p(y=1|x))^{(1-y)}}\tag{7}$
式（7）取似然函数为：
$L(\theta)=\prod^m_{i=1}{p(y_i|x_i;\theta)}=\prod^m_{i=1}{p(y_i=1|x_i;\theta)^y_i}{(1-p(y_i=1|x_i;\theta))^{(1-y_i)}}\tag{8}$
对数似然函数为：
$l(\theta)=logL((\theta) =log\prod^m_{i=1}{p(y|x_i;\theta)}=\sum^m_{i=1}{[y_ilog(p(y=1|x_i;\theta))+(1-y_i)log(1-p(y=1|x_i;\theta))]}\tag{9}$
       最大似然估计就是求使 $l(θ)$取最大值时的 $θ$，其实这里可以使用梯度上升法求解，求得的 $θ$就是要求的最佳参数，在Andrew Ng的课程中将 $J(θ)$取为下式：
$J(\theta)=-\frac{1}{m}l(\theta)$
       因为 $l(\theta)$前加有负号，所以，只需求得 $\theta$使得 $J(\theta)$最小即可。

算法

        $J(\theta)$是凸函数，我们可以用梯度下降法来进行优化求得 $\theta$的值。
下面是具体的推导过程：

       上式与线性回归中的梯度下降函数形式一模一样，但其实是不一样的，因为在LR模型中， $h_{\theta}(x)$与线性回归是不一样的。
       梯度下降，即 $\theta$的更新过程为：
                                                        
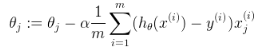
参考：
https://blog.csdn.net/jk123vip/article/details/80591619
https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://www.tuicool.com/articles/uiMjyuu
西瓜书