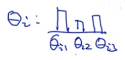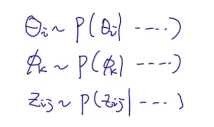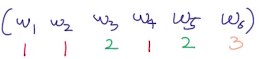24[NLP训练营]从LDA文章生成到Gibbs吉布斯采样

公式输入请参考： 在线Latex公式

前言

要搞清楚Gibbs，先要搞清楚通过LDA方法文章是怎么生成的，再反过来考虑怎么从文章里面训练模型，学习参数。
生成文章是一个过程，即process。我们的目标是生成document。也就是用一个生成模型来干这个事情。
从看不见的参数集合，生成看得见的文档。如果是从文档反推是什么参数生成我们的文档，这个过程就是inference。

LDA文章的生成过程（非官方）

第一步：确定主题
这个步骤有两种情况：
a：一个文章只有一个主题（朴素贝叶斯干这个事）
b：一个文章以后多个主题（这个是我们要讨论的）

第二步：根据主题的分布，生成文章，也就是要生成一堆的单词（类似LDA是不考虑单词的顺序的）
词表是已知的：

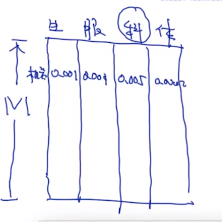
过程大概如下：

生成过程了解了以后，就是理解反向的过程：
我们现在有文档，反推词表分布概率和主题分布概率。文档不需要任何的标注。

生成的例子

假设已知：

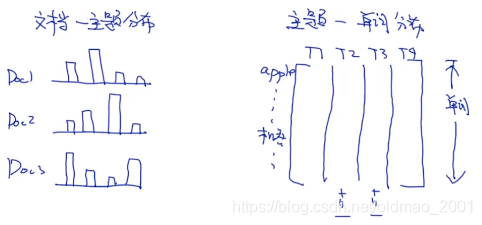
例如生成文档1（Doc1），它的主题分布对应的参数为 $\theta_1$，用这个参数来采样主题，例如：

然后根据这些个主题生成单词：

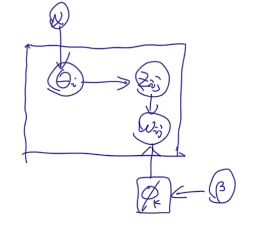
文章的生成（官方）

K：主题的个数
N：要生成的文章数量
$N_i$：文章i中的单词数量
$\theta_i$：文章i的主题分布（模型参数）
$Z_{ij}$：第i个文章中第j个单词的主题（隐变量）
$\alpha,\beta$是超参数，分别生成 $\theta$（所有文章的 $\theta$都是同一个 $\alpha$生成的）和 $\phi$：词的分布（模型参数）

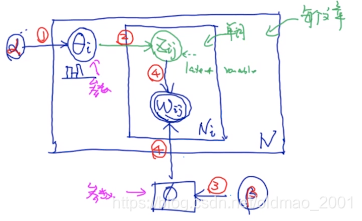
每个方框代表一个循环，单词 $w_{ij}$由两个东西决定，一个是 $Z_{ij}$，一个是 $\phi$

1.alpha生成theta

首先一个条件是所有的 $\theta_i$对应的主题分布概率累加和为1.
例如：
这个文章主题有3个：

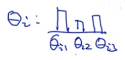
这里 $\theta_{i1}+\theta_{i2}+\theta_{i3}=1$
第二个条件是： $\theta_{ij}\in [0,1]$
要想生成这样的一个分布就是用狄利克雷Dirichlet distribution分布（当然还有别的方法来做这个事情，例如： $\theta_i=softmax(\theta_i)$，但是狄利克雷分布比较好计算）。记为：
$\theta_i\sim Dir(\alpha)$
这里有介绍，要翻墙
https://en.wikipedia.org/wiki/Dirichlet_distribution

3.beta生成phi

跟上面一样的，每个 $\phi_k$的分布累加为1， $\phi_{ki}\in [0,1]$，记为：
$\phi_k\sim Dir(\beta)$

2.theta_i生成Z_ij

$Z_ij\sim Multinomial(\theta_i)$
如果i=3，那么：

4.Z_ij和phi生成w_ij

$w_ij\sim Multinomial(\phi_{Z_{ij}})$

整体生成过程

Gibbs sampling

Gibbs sampling的由来

由于上面的分析可知，如果要反向估计 $\{\theta,\phi,Z\}$，也就是要求：
$P(\theta,\phi,Z|w,\alpha,\beta)$
这个是很难求的，只能用近似的方法来求，大概意思就是通过采样来近似，这个方法就是Gibbs sampling。
同时采样多个参数 $\{\theta,\phi,Z\}$是很困难的，把它展开：
$\{\theta_1,\theta_2,...\phi_1,\phi_2,...Z_1,Z_2,...\}$
这个时候如果采样 $\theta_1$，那么我们假定其他参数是已知的。以此类推。

theta_i的采样

根据上面的分析，可以写为：
$\theta_i\sim P(\theta_i|\alpha,Z,w,\phi,\beta)$
根据Markov Blanket定理，就是不直接相关的条件可以去掉，例如：

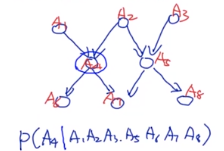
这里和A4不直接相关的A8，A3等可以从条件概率中去掉，他们两个的信息包含在了A5里面，所以A5保留，A6A7是由A4生成的，也保留。最后变成：P(A4|A1A2A5A6A7)

因此，根据上图的生成关系，上面的 $\theta_i$可以写为：
$\theta_i\sim P(\theta_i|\alpha,Z,w,\phi,\beta)\\ =P(\theta_i|\alpha,Z)$
由于 $\theta_i$只依赖于当前文章的单词，所以其他文章的单词，或者说主题可以不要：
$\theta_i=P(\theta_i|\alpha,Z_{i\cdot})$
上面的概率是已知条件中的 $\alpha,Z_{i\cdot}$，求 $\theta_i$，是明显的后验概率的形式，因此根据我们在学习签名MAP的经验，知道，后验概率正比于likelyhood*先验概率
这里面likelyhood就是用 $\theta_i$观察到 $Z_{i\cdot}$的概率（写出来就是 $P(Z_{i\cdot}|\theta_i)$，这个就是上面提到的multinomial），先验概率则是用 $\alpha$生成 $\theta_i$的概率（写出来就是 $P(\theta_i|\alpha)$这个就是上面提到的狄利克雷分布 $\theta_i\sim Dir(\alpha)$），因此可以得到：
$\theta_i\propto P(\theta_i|\alpha)P(Z_{i\cdot}|\theta_i)$
根据狄利克雷的PDF（概率密度函数）进行展开

上图来自百度百科
$P(\theta_i|\alpha)=\cfrac{1}{\Beta(\alpha)}\prod_{k=1}^K\theta_{ik}^{\alpha_{k-1}}$
多项式分布（Multinomial Distribution）也可以展开
$P(Z_{i\cdot}|\theta_i)=\prod_{j=1}^{N_i}\prod_{k=1}^K\theta_{ik}^{I(Z_{ij=k})}$
$I(Z_{ij=k})$表示当 $Z_{ij=k}$成立时表达式为1，否则为0.
整理合并：
$\theta_i\propto\cfrac{1}{\Beta(\alpha)}\prod_{k=1}^K\theta_{ik}^{\alpha_{k-1}}\prod_{j=1}^{N_i}\prod_{k=1}^K\theta_{ik}^{I(Z_{ij=k})}\\ =\cfrac{1}{\Beta(\alpha)}\prod_{k=1}^K\theta_{ik}^{\sum_{j=1}^{N_i}I(Z_{ij=k})+\alpha_{k-1}}\\ =Dir(\alpha+\sum_{j=1}^{N_i}I(Z_{ij=k}))$
下面来说下这个公式的意思，现有一个狄利克雷分布来产生参数，然后由观测数据( $\sum_{j=1}^{N_i}I(Z_{ij=k})+\alpha_{k-1}$)来对参数进行修正。例如刚开始由 $\alpha$生成的参数 $\theta_i\sim Dir(\alpha)$是这个样子： $\alpha=(1,1,1,1)$
然后在第i个文章中，有 $n_{ij}$个单词背分类为主题j，例如： $n_{i1}=2,n_{i2}=3,n_{i3}=2,n_{i4}=3,$
修正后： $\alpha=(1+2,1+3,1+2,1+3)=(3,4,3,4)$
最后小结， $\theta_i$的估计可以写为：
$\theta_i\sim Dir(\alpha+\sum_{j=1}^{N_i}I(Z_{ij=k}))$

Z的采样

用上面 $\theta_i$的套路，写出Z的概率
$P(Z_{ij}=k|w_{ij},\phi_k,\theta_i)\propto P(Z_{ij}=k|\theta_i)\cdot P(w_{ij}|Z_{ij}=k,\phi_k)\\ =\theta_{ik}\cdot\phi_{k,w_{ij}}=exp(log\theta_{ik}+log\phi_{k,w_{ij}})$
phi的采样略了。。。

小结

吉布斯采样的思想和之前在讲LASSO的时候提到过一个东西很相似，就是coordinate descent，就是固定其他变量，求其中一个变量。吉布斯采样可以用在所有的贝叶斯估计中


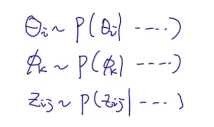
这个算法是有缺点的：就是参数个数比较多（例如： $Z_{ij}$是和文档中的单词个数有关）
因此我们要想，到低有没有必要对所有的参数进行采样？
其实有些情况是不必要的，例如：一个文档中有6个单词：

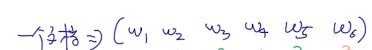
每个单词所属的主题分别是：

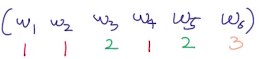
以上就是相当于 $Z_{ij}$是知道的， $Z_{ij}$就是单词主题的分布，我们就可以用 $Z_{ij}$来估计参数 $\theta_i$(文章主题的分布)：

类似也可以用 $Z_{ij}$来估计 $\phi$
这样的方式就叫做collapsed gibbs sampling。上面用 $Z_{ij}$来估计参数 $\theta_i$和 $\phi$的过程就叫collapsed 或者Integral。（从概率上来看实际就是边缘化的操作）

collapsed gibbs sampling

下图是LDA生成的过程。

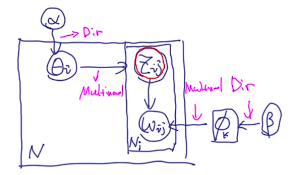
为了更好描述collapsed gibbs sampling。把里面的标识换一下，问题的描述变成：
计算 $P(Z_{ts}|Z_{-ts},w,\alpha,\beta)$
t代表第t个文档
s代表第t个文档的第s个单词

---

假设有一个集合
$x=\{x_1,x_2,...x_n\}$
那么它可以表示为：
$x=x_i\cup x_{-i}$
同样的，问题描述中的 $Z=Z_{ts}\cup Z_{-ts}$

---

第一步

可以看到，问题描述中是没有 $\phi,\theta$的，我们就是要用collapsed 的方式把这两个变量进行边缘化，
$P(Z_{ts}|Z_{-ts},w,\alpha,\beta)=\cfrac{P(Z,w|\alpha,\beta)}{P(Z_{-ts},w|\alpha,\beta)}$

---

上面的式子为什么会相等呢？
$\cfrac{P(Z,w|\alpha,\beta)}{P(Z_{-ts},w|\alpha,\beta)}*\cfrac{P(\alpha,\beta)}{P(\alpha,\beta)}\\ =\cfrac{P(Z,w,\alpha,\beta)}{P(Z_{-ts},w,\alpha,\beta)}\tag1$
$P(Z_{ts}|Z_{-ts},w,\alpha,\beta)*P(Z_{-ts},w,\alpha,\beta)\\ =P(Z_{ts},Z_{-ts},w,\alpha,\beta)=P(Z,w,\alpha,\beta)\tag2$
把公式2代入1就得到上面的等式了。

---

第二步 看分子

把第一步中的分子分母分开看，先看分子
$P(Z,w|\alpha,\beta)$
如果要把 $\phi,\theta$边缘化就是要写成下面的积分：
$P(Z,w|\alpha,\beta)=P(Z|\alpha)\cdot P(w|Z,\beta)\\ =\int P(Z|\theta)\cdot P(\theta|\alpha)d\theta\int P(w|Z,\phi)\cdot P(\phi|\beta)d\phi$
分别看这两项积分：

第一项

第一项中 $P(Z|\theta)$相当于multinomial分布， $P(\theta|\alpha)$相当于狄利克雷分布，因此：
$\int P(Z|\theta)\cdot P(\theta|\alpha)d\theta=\int\prod_{i=1}^N\prod_{j=1}^{N_i}\prod_{k=1}^K\theta^{I(Z_{ij=k})}_{ik}\cdot\prod_{i=1}^N\cfrac{1}{\Beta(\alpha)}\prod_{k=1}^K\theta_{ik}^{\alpha_{k-1}}d\theta_k\\ =\prod_{i=1}^N\int\prod_{j=1}^{N_i}\prod_{k=1}^K\theta^{I(Z_{ij=k})}_{ik}\cdot\cfrac{1}{\Beta(\alpha)}\prod_{k=1}^K\theta_{ik}^{\alpha_{k-1}}d\theta_k$
这里把连乘 $\prod_{j=1}^{N_i}$放到指数变成累加 $\sum_{j=1}^{N_i}$，然后和后面的 $\theta_{ik}^{\alpha_{k-1}}$的指数进行相加，上式变为：
$=\prod_{i=1}^N\cfrac{1}{\Beta(\alpha)}\int\prod_{k=1}^K\theta^{\sum_{j=1}^{N_i}I(Z_{ij=k})+\alpha_{k-1}}_{ik}d\theta_k\tag3$
根据狄利克雷分布的概念：
$Dir(\theta|\alpha)=\cfrac{1}{\Beta(\alpha)}\prod_{k=1}^K\theta_{ik}^{\alpha_{k-1}}$
可以看到公式3其实是狄利克雷分布，最后变成：
$(3)=\prod_{i=1}^N\cfrac{\Beta(\alpha+\sum_{j=1}^{N_i}I_k(Z_{ij}))}{\Beta(\alpha)}\tag4$
这里给个例子看看 $\sum_{j=1}^{N_i}I_k(Z_{ij})$是怎么算，例如一个文档里面有六个词，每个词对应的主题 $Z_{ij}$如下

$w_{i1}$	$w_{i2}$	$w_{i3}$	$w_{i4}$	$w_{i5}$	$w_{i6}$
$z_{i1}$	$z_{i2}$	$z_{i3}$	$z_{i4}$	$z_{i5}$	$z_{i6}$
1	1	2	3	2	2

也就是主题为1的有2个词，为2的有3个词，为3的有1个词，因此 $\sum_{j=1}^{N_i}I_k(Z_{ij})=(2,3,1)$
公式4中 $\alpha$通常是一个向量，可以写作： $(\alpha_1,\alpha_2,\alpha_3,...)$
公式4中的分子就变成了 $\Beta(\alpha_1+2,\alpha_2+3,\alpha_3+1)$，分母变成了 $\Beta(\alpha_1,\alpha_2,\alpha_3)$

第二项

$\int P(w|Z,\phi)\cdot P(\phi|\beta)d\phi$
跟第一项类似的，是一个multinomial和dirichlet分布相乘，经过上面的证明我们知道这两个东西相乘结果还是一个dirichlet分布。上式：
$=\int\prod_{k=1}^K\prod_{i:Z_i=k}\prod_{v=1}^V\phi_{k,v}^{I(w_i=v)}\cdot\prod_{k=1}^K\cfrac{1}{\Beta(\beta)}\prod_{v=1}^V\phi_{k,v}^{\beta_v-1}d\phi_k$
这里的 $i:Z_i=k$意思是所有的单词i是属于主题k的，另外也可以吧连乘变成指数上的累加：
$=\prod_{k=1}^K\cfrac{1}{\Beta(\beta)}\int\prod_{v=1}^V\phi_{k,v}^{\sum_{i:Z_i=k}I(w_i=v)+\beta_v-1}d\phi_k\\ =\prod_{k=1}^K\cfrac{\Beta(\beta+\sum_{i:Z_i=k}I_v(w_i))}{\Beta(\beta)}$

联合第一、第二项

$P(Z,w|\alpha,\beta)=第一项\cdot 第二项\\ =\prod_{i=1}^N\cfrac{\Beta(\alpha+\sum_{j=1}^{N_i}I_k(Z_{ij}))}{\Beta(\alpha)}\cdot \prod_{k=1}^K\cfrac{\Beta(\beta+\sum_{i:Z_i=k}I_v(w_i))}{\Beta(\beta)}$

第二步 看分母

$P(Z_{-ts},w|\alpha,\beta)$
也就是不考虑 $Z_{ts}$
$P(Z_{-ts},w|\alpha,\beta)=\prod_{i=1}^N\cfrac{\Beta(\alpha+\sum_{j=1,\delta_j\neq(t,s)}^{N_i}I_k(Z_{ij}))}{\Beta(\alpha)}\cdot \prod_{k=1}^K\cfrac{\Beta(\beta+\sum_{i:Z_i=k,\delta_j\neq(t,s)}I_v(w_i))}{\Beta(\beta)}$
$\delta_j$代表当前单词所在的位置

分子分母同时看

$P(Z_{ts}|Z_{-ts},w,\alpha,\beta)=\cfrac{分子}{分母}$
可以看到分子和分母除了第t个文档，其他项是一样的，由于最外面是连乘，所以可以都消掉：
$P(Z_{ts}|Z_{-ts},w,\alpha,\beta)=\cfrac{\Beta(\alpha+\sum_{j=1}^{N_i}I_k(Z_{ij}))}{\Beta(\alpha+\sum_{j=1,j\neq s}^{N_i}I_k(Z_{ij}))}\cfrac{\Beta(\beta+\sum_{i:Z_i=k}I_v(w_i))}{\Beta(\beta+\sum_{i:Z_i=k,\delta_j\neq(t,s)}I_v(w_i))}$
下面就是利用 $\Beta$函数来进行简化。

化简

用例子来看上面的
$\cfrac{\Beta(\alpha+\sum_{j=1}^{N_i}I_k(Z_{ij}))}{\Beta(\alpha+\sum_{j=1,j\neq s}^{N_i}I_k(Z_{ij}))}$
的分子和分母
先看分子 $\sum_{j=1}^{N_i}I_k(Z_{ij})$是怎么算，例如一个文档里面有六个词，每个词对应的主题 $Z_{ij}$如下

$w_{i1}$	$w_{i2}$	$w_{i3}$	$w_{i4}$	$w_{i5}$	$w_{i6}$
$z_{i1}$	$z_{i2}$	$z_{i3}$	$z_{i4}$	$z_{i5}$	$z_{i6}$
1	1	1	2	3	2

也就是主题为1的有3个词，为2的有2个词，为3的有1个词，因此 $\sum_{j=1}^{N_i}I_k(Z_{ij})=(3,2,1)$
上式中 $\alpha$通常是一个向量，可以写作： $(\alpha_1,\alpha_2,\alpha_3,...,\alpha_k)$
因此上式的分子就变成了 $\Beta(\alpha_1+3,\alpha_2+2,\alpha_3+1)$。
由于分母不包含当前词的主题，当当前词是 $w_{i1}$的时候，分母变成了 $\Beta(\alpha_1+2,\alpha_2+2,\alpha_3+1)$
因此：
$\cfrac{\Beta(\alpha+\sum_{j=1}^{N_i}I_k(Z_{ij}))}{\Beta(\alpha+\sum_{j=1,j\neq s}^{N_i}I_k(Z_{ij}))}=\cfrac{\Beta(\alpha_1+n_{t1},\alpha_2+n_{t2}+...+\alpha_k+n_{kt1})}{\Beta(\alpha_1+n'_{t1},\alpha_2+n'_{t2}+...+\alpha_k+n'_{kt1})}\tag5$
$n_{ti}$表示第t个文档有多少单词被分配主题i
$n'_{ti}$表示去掉 $Z_{ts}$后，第t个文档有多少单词被分配主题i
这里的分子分母都有k项，而且只有一项不一样。
继续化简前先给出 $\Beta$函数的形式：

因此： $\Beta(\alpha_1,\alpha_2,\alpha_3,...,\alpha_k)=\cfrac{\prod_{k=1}^K(\Gamma(\alpha_k)}{\Gamma(\sum_{k=1}^K\alpha_k)}$
$(5)=\cfrac{\prod_{k=1}^K(\Gamma(\alpha_k+n_{tk}))}{\Gamma(\sum_{k=1}^K(\alpha_k+n_{tk}))}\cdot\cfrac{\Gamma(\sum_{k=1}^K(\alpha_k+n'_{tk}))}{\prod_{k=1}^K(\Gamma(\alpha_k+n'_{tk}))}$
伽玛函数： $\Gamma(n)=(n-1)!$，而且上面提到过 $\alpha_k+n_{tk}$和 $\alpha_k+n'_{tk}$都有k项，而且只有一项不一样。例如：
当 $Z_{ts}=2$，则 $n_{t2}-n'_{t2}=1$且 $n_{ti}=n'_{ti},i\neq2$，因此：
$(5)=\cfrac{\prod_{k=1}^K(\Gamma(\alpha_k+n_{tk}))}{\prod_{k=1}^K(\Gamma(\alpha_k+n'_{tk}))}\cdot\cfrac{\Gamma(\sum_{k=1}^K(\alpha_k+n'_{tk}))}{\Gamma(\sum_{k=1}^K(\alpha_k+n_{tk}))}\\ =\cfrac{\alpha_k+n_{tu}^{new}}{\sum_{k=1}^K\alpha_k+n_t^{new}}\cdot \cfrac{\beta_{w_i}+n_{uw_i}^{new}}{\sum_{v=1}^V\beta_v+n_u^{new}}$
$n_{tu}^{new}$表示当前第t个文档有多少个单词被分配到主题u（丢掉 $Z_{ts}$，不考虑当前词）
$n_t^{new}$表示当前第t个文档的单词数量（丢掉 $Z_{ts}$，不考虑当前词）
$n_{uw_i}^{new}$表示对于单词 $w_i$有多少次被分配到了主题u（丢掉 $Z_{ts}$，不考虑当前词）
$n_u^{new}$表示所有文档中有多少单词分配到了主题u（丢掉 $Z_{ts}$，不考虑当前词）

小栗子

假设有两个文档：

主题数量k为3，词库大小为4.
先随机初始化每个单词的主题。

超参数 $\alpha=(0.1,0.1,0.1),\beta=(0.1,0.1,0.1,0.1)$
下面按化简后的公式来进行计算第一个文档的第一个单词：

这个时候把第一个单词【今天】从文档1中去掉，可以看到 $n_{1,1}^{new}=2$（就是还有2个单词分配到主题1）， $n_1^{new}=6$（还剩下6个单词）
因为每一个单词在不同文档可以有不同的主题，也就是有不同的主题概率分布，因此：把第一个单词【今天】从文档1中去掉，没有【今天】分配到主题1，因此 $n_{1,w_1}^{new}=0$，但是除了第一个单词【今天】外，分配到主题1的单词有3个，因此 $n_1^{new}=3$
$P(Z_{1,1}=1|Z_{-(1,1)},w,\alpha,\beta)=\cfrac{0.1+2}{0.1+0.1+0.1+6}\cdot \cfrac{0.1+0}{0.1+0.1+0.1+0.1+3}$
同理：
$P(Z_{1,1}=2|Z_{-(1,1)},w,\alpha,\beta)=\cfrac{0.1+2}{0.1+0.1+0.1+6}\cdot \cfrac{0.1+1}{0.1+0.1+0.1+0.1+5}$
$P(Z_{1,1}=3|Z_{-(1,1)},w,\alpha,\beta)=\cfrac{0.1+2}{0.1+0.1+0.1+6}\cdot \cfrac{0.1+2}{0.1+0.1+0.1+0.1+4}$
计算完毕后，进行归一化得到（使得累加等于1）：

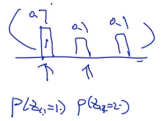
然后就可以进行multinomial采样。

小结

$P(Z_{ts}|Z_{-ts},w,\alpha,\beta)=\cfrac{\alpha_k+n_{tu}^{new}}{\sum_{k=1}^K\alpha_k+n_t^{new}}\cdot \cfrac{\beta_{w_i}+n_{uw_i}^{new}}{\sum_{v=1}^V\beta_v+n_u^{new}}$
右边的第一项代表一个文档中的单词的主题分类，当一个文档中的单词分类越集中，主题也越集中，例如一个文档中的有10个单词，前面9个都是主题1，那么第十个单词也会倾向于采样为第1个主题。
第二项是所有文档中某个单词的主题分类影响，例如所有文章中某个单词出现100次，80次是主题1，那么该单词被抽样为主题1的概率越大。