数论整理之欧拉函数

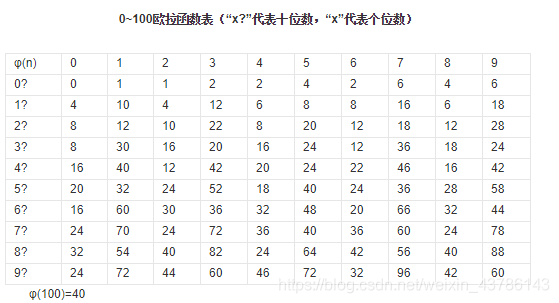
在数论，对正整数n，欧拉函数是小于n的正整数中与n互质的数的数目（φ(1)=1）

通式：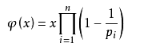
ps：那个不认识的符号是累乘 …… 卑微
其中p1, p2……pn为x的所有质因数，x是不为0的整数。
φ(1)=1（和1互质的数(小于等于1)就是1本身）。
注意：每种质因数只一个。 比如12=223那么φ（12）=φ（4 * 3）=φ（2 ^ 2 * 3 ^ 1）=（2 ^ 2-2 ^ 1）*（3 ^ 1-3 ^ 0）=4
若n是质数p的k次幂， ，因为除了p的倍数外，其他数都跟n互质。
设n为正整数，以 φ(n)表示不超过n且与n互素的正整数的个数，称为n的欧拉函数值
φ：N→N，n→φ(n)称为欧拉函数。
欧拉函数是积性函数——若m,n互质，
特殊性质：当n为奇质数时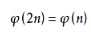， , 证明与上述类似。
若n为质数则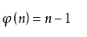

//标程
//欧拉函数
#include<iostream>
#include<cstdio>
using namespace std;

#define ll long long int
#define MAX 2000000+5

int euler[MAX];

void Euler(){
    for(int i=2;i<MAX;i++)
        euler[i] = i;

    for(int i=2;i<MAX;i++){
        if(euler[i]==i)
            for(int j=i;j<MAX;j+=i)
            euler[j] = euler[j]/i*(i-1);
    }
}

int main(){
    Euler();
    int n;
    euler[1] = 1;//这里要初始化euler[1] = 1;
    for(int i = 0;i < 20;i++)
    {
        cout<<euler[i]<<endl;
    }
	return 0;
}

例题：

#include<iostream>
#include<cstdio>
using namespace std;

#define ll long long int
const int MAX = 1000010;

int euler[MAX];
void Euler(){
    for(int i=2;i<MAX;i++)
        euler[i] = i;

    for(int i=2;i<MAX;i++){
        if(euler[i]==i)
            for(int j=i;j<MAX;j+=i)
            euler[j] = euler[j]/i*(i-1);
    }
}

int main(){
    Euler();
    int T,n,a,cnt=1;
    ll ans;
    scanf("%d",&T);
    while(T--){
            ans = 0;
        scanf("%d",&n);
        while(n--){
            scanf("%d",&a);
            for(int i=a+1;;i++)
                if(euler[i]>=a){
                    ans+=i;
                    break;
                }
        }
        printf("Case %d: %lld Xukha\n",cnt,ans);
        cnt++;
    }
	return 0;
}