数论之————欧拉函数

再讲欧拉函数之前，先讲一下欧拉定理。

欧拉定理，也称费马-欧拉定理
若n,a为正整数，且n,a互质，即gcd(a,n) = 1，则
a^φ(n) ≡ 1 (mod n)。
————————————————————————————————————————————————————
这里的φ(n)就是欧拉函数。表达的意思是1到n-1内与n互质的数的个数。
正整数n的唯一分解式n=p1^a1*p2^a2…..p1,p2都是n的质因子。要求1，2，3…n与n互素的数的个数，分别减去是p1，p2…pk,的倍数的个数。
得到：n-n/p1-n/p2…-n/pk。
欧拉函数公式：

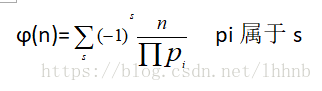
然后同时加上是两个素因子的倍数的个数，这就是容斥原理。（因为重复减了）n/p1*p2+n/p1*p3…
对于是加号还是减号取决于素因子个数，奇减偶加。
比如：是两个素因子的倍数的数是加，是三个素因子的倍数的数是减
再简化一下
φ(n)=n(1-1/p1)*(1-1/p2)…(1-1/pk);

只求一个数的欧拉函数代码模板：

int euler_phi(int n){
   int m=(int)sqrt(n+0.5);
   int ans=n;
   for(int i=2;i<=m;i++)
   if(n%i==0){
   ans=ans/i*(i-1);      //最后的化简公式n(1-1/p)
   while(n%i==0) n/=i;
   }
   if(n>1) ans=ans/n*(n-1);
   return ans;
   }

1~n所有数的欧拉函数值。类似埃筛。

代码：

void euler(int n,int *phi)
{
    memset(phi,0,sizeof(phi));
    phi[1]=1;
    for(int i=2;i<=n;i++)
    {
        if(!phi[i])
        {
            for(int j=i;j<=n;j+=i)
            {
                if(!phi[j])
                    phi[j]=j;
            phi[j]=phi[j]/i*(i-1);
            }
        }
    }
}