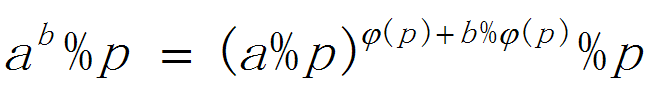数论之欧拉函数+欧拉线性筛

以下资料整理来自：https://www.cnblogs.com/linyujun/p/5194170.html

                                https://blog.csdn.net/YxuanwKeith/article/details/52387873

void Getphi(int Max) {
    phi[1] = 1;
    for (int i = 2; i <= Max; i ++) {
        if (!Flag[i]) {
            phi[i] = i - 1; // i是质数，第一种情况。
            pri[++ pri[0]] = i;
        }
        for (int j = 1; j <= pri[0]; j ++) {
            if (1ll * i * pri[j] > Max) break;
            Flag[i * pri[j]] = 1; //筛质数。
            if (i % pri[j] == 0) {
                phi[i * pri[j]] = phi[i] * pri[j];//（i % pri[j] = 0），第二种情况
                break;
            }
            phi[i * pri[j]] = phi[i] * (pri[j] - 1); //（i % pri[j] ！= 0），第三种情况
        }
    }
}

long long Getphi(long long n) {
    long long phi = n;
    for (long long i = 2; i * i <= n; i ++) {
        if (n % i == 0) {
            phi /= i;
            phi *= i - 1;
            while (n % i == 0) n /= i;
        }
    }
    if (n != 1) phi /= n, phi *= n - 1;
    return phi;
}

a^b % p  不等价  (a%p)^(b%p) % p

因为           a^φ(p) ≡ 1 (mod p)    所以     a^b % p  =  (a%p)^(b%φ(p)) % p

（欧拉函数前提是a和p互质）

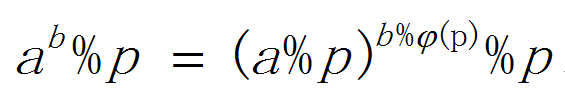
如果p是质数

直接用这个公式

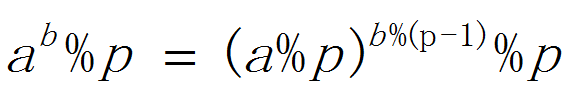
发现了一个新公式，貌似可以摆脱a和p互质的束缚，让我们来命名为：超欧拉取模进化公式