导数、微分、积分的几何理解
一、导数
-
导数的定义
设函数 在点 的某领域内有定义,若极限 存在,则称函数 在点 处可导,并称该极限为函数 在点 处的导数,记做 。
令 ,则 式可改写为 所以,导数式函数增量 与自变量增量 之比 的极限。这个增量比称为函数关于自变量的平均变化率(又称商差),而导数 则为 在 处关于 的变化率。 -
导数的几何意义
在导数的定义中已经说过,导数 为 在 处关于 的变化率;所以导数的几何意义就是切线(斜率)。
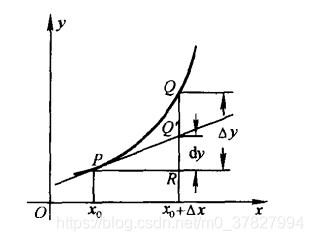
对应下图,直线 就是函数 在 处的导数(切线),即
二、微分
-
微分的定义
设函数 定义在点 的某邻域 内。当给 一个增量 时,相应的得到函数的增量为 如果存在常数 ,使得 能表示成 则称函数 在点 可微,并称(3)式中的第一项 为 在点 处的微分,记做 由定义可见函数的微分与增量仅差一个关于 的高阶无穷小量,由于 是 的线性函数,所以当 时,也说微分 是增量 的线性主部。 -
微分的几何意义
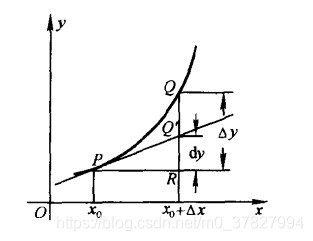
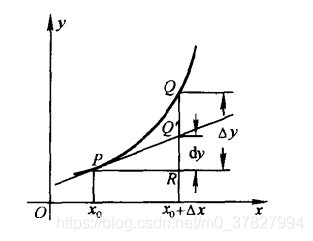
微分的几何意义如下图所示,当自变量由 增加到 时,函数增量 ;
而微分则是在点 处的切线上与 所对应的增量
其中, 对应的是 (高阶无穷小量),即
三、积分
-
积分的定义
设 是定义在 上的一个函数,对于 的一个分割 ,任取点 ,并做和式
称此和式为函数 在 上的一个积分和,也称黎曼和。
定积分:
其中, 称为被积函数, 称为积分变量, 称为积分区间。 -
积分的几何意义
由上文积分的定义可知,积分的几何意义就是求面积。
对应下图, 的几何意义就是曲线 和 轴围成的面积。