只讲一些导数在OI中的简单应用,特别基础的东西,不会很详细也不会很全面。
导数的定义
设函数\(y=f(x)\)在点\(x_0\)的某个邻域内有定义,当自变量\(x\)在\(x_0\)处有增量\(Δx\),\((x_0+Δx)\)也在该邻域内时,相应地函数取得增量\(Δy=f(x0+Δx)-f(x0)\),如果\(Δy\)与\(Δx\)之比当\(Δx→0\)时极限存在,则称函数\(y=f(x)\)在点\(x_0\)处可导,并称这个极限为函数\(y=f(x)\)在点\(x_0\)处的导数,记作\(f'(x_0)\),即:
\[f'(x_0)=\lim \limits_{\Delta x \to 0} \frac{\Delta y}{\Delta x}=\lim \limits_{\Delta x \to 0} \frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}\]
如果函数\(y=f(x)\)在开区间内每一点都可导,就称函数\(f(x)\)在区间内可导。这时函数\(y=f(x)\)对于区间内的每一个确定的\(x\)值,都对应着一个确定的导数值,这就构成一个新的函数,称这个函数为原来函数\(y=f(x)\)的导函数,记作\(f'(x)\)。
不严谨地说,导数其实就是函数在每个点上的斜率(不要吐槽)。
关于导数的四则运算
\[(f(x)+g(x))'=f'(x)+g'(x)\]
\[(f(x)-g(x))'=f'(x)-g'(x)\]
\[(f(x)g(x))'=f'(x)g(x)+f(x)g’(x)\]
\[(\frac{f(x)}{g(x)})'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}\]
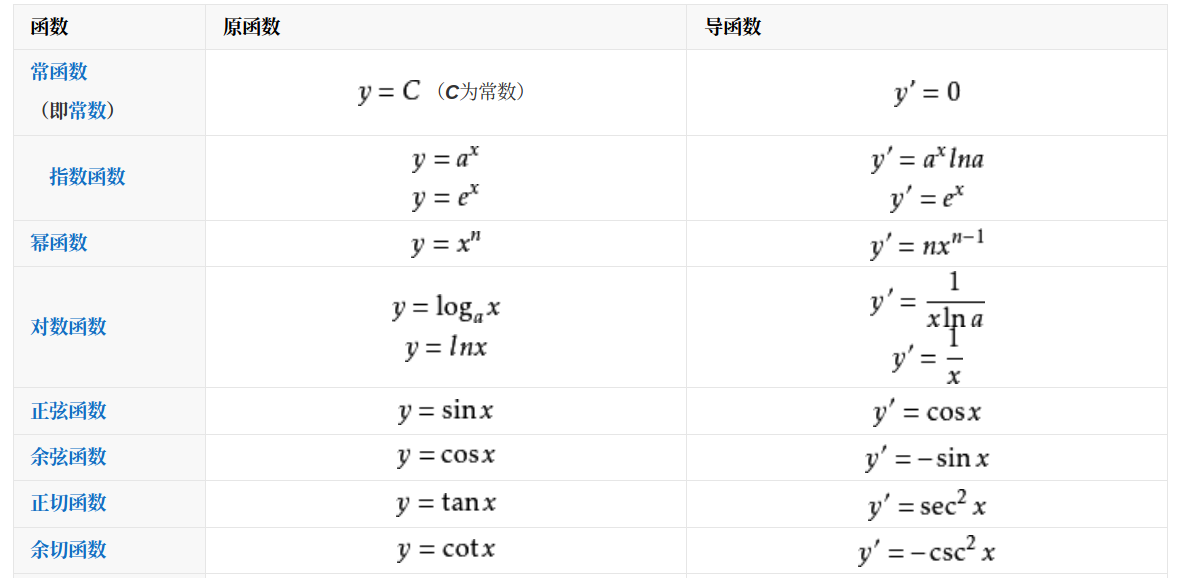
常见函数的导数
ErkkiErkko懒的打公式了,直接在百度百科上截了一张下来。
微积分基本定理(牛顿-莱布尼茨公式)
\[\int_{a}^{b}f'(x)\,dx=f(b)-f(a)\]
泰勒展开
由于博主姿势水平不够就先放几个柿子之后再填坑吧。
\[e^x=1+\frac{1}{1!}x+\frac{1}{2!}x^2+\frac{1}{3!}x^3+...\]
\[sin(x)=x-\frac{1}{3!}x^3+\frac{1}{5!}x^5-...\]
\[cos(x)=1-\frac{1}{2!}x^2+\frac{1}{4!}x^4+...\]
\[ln(1+x)=x-\frac{1}{2}x^2+\frac{1}{3}x^3-...\]
\[\frac{1}{1-x}=1+x+x^2+x^3+...\]
\[(1+x)^a=1+\frac{a}{1!}x+\frac{a(a-1)}{2!}x^2+\frac{a(a-1)(a-2)}{3!}x^3+...\]