第六章基本符号演算和微分方程
主要内容:
- 计算极限
- 求导数
- 求常微分方程(ODE)的解析解和数值解
- 求积分
计算极限
命令一般形式:limit(f,m,direction)
f : 需要计算极限的表达式,f中的变量必须使用syms定义,否则会因为无法识别而报错
m: 指明计算f趋近于m时的极限,如果不填,默认是0
direction: 是一个字符串,值有’left’,’right’和不填 ,分别代表求左极限,右极限,和默认求极限
计算导数
命令:diff(f,n)
f : 需要求的原函数 ,必须将变量声明为 syms
n : 要求的几阶导
解常微分方程的解析解
命令一般形式:dsolve(f1,f2,…fn,’cond1’,’cond2’,……’condn’)
fn : 一个字符串, 内容是方程的表达式 ,
f1到fn 表示求解方程组
condn : 字符串,内容是初始条件的表达式
例:
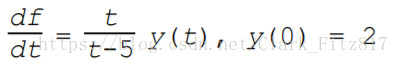
dsolve(‘Dy = y*t/(t-5)’,’y(0)=2’);
二阶导用 D2表示
注意 默认地,dsolve 使用 t 作为独立变量。我们可以告诉它使用其它变量——在命令行的
末尾附带上我们要使用的独立变量
解常微分方程的数值解
这个需要说明解析解和数值解的区别:
解析解意思是解可以用表达式具体的写出来,而数值解是只能得到点对,无法得到解析式,因为不是所有的常微分方程都有解析解,大部分只能得到数值解
解数值解用到的命令是
ode23()和ode45()两种
这两个函数都使用(龙格-库塔)法来数值解,区别是ode45比ode23阶数更高,对应的ode45的精度也比ode23高
两个函数的调用方式完全相同
[t,y] = ode23(‘func_name’, [start_time, end_time], y(0))
func_name 是在单独的.m文件中定义的方程函数
[start_time, end_time] 是求解区间
y(0)是初值
如果要求解二阶的常微分方程,需要将二阶方程通过换元转换为一阶方程组
% 例如 求方程 y'' + 16y = sin(4.3t)当 y(0) = y'(0) = 0 时的解。
% 换元:令x1 = y;
% x2 = y';
% 定义微分方程函数
%创建数组储存数据
xdot = zerot(2,1);
% 列方程组
xdot(2) = sin(4.3*t)-16*x(1);
xdot(1) = x(2);
% 调用函数
[t,x] = ode23('fun',[0 2*PI],[0,0]);
% x(:,1) 是 y 的解
% x(:,2) 是 y' 的解
plot(t,x(:,1)); % 画出数值解的图像求积分
一般形式的命令:
int(f,v)
f 需要求积分的表达式,可以是字符串,也可以是变量表达式
v(可选) 是指定的变量,如果表达式中有多个变元,没有指定时会默认其中的一个符号为变量
注意matlab给出的积分省略了常数部分,在写结果时需要加上
求定积分
一般形式的命令:
int(f,v,end,start)
f : 同求积分
v: 同求积分
end 定积分的上界
start 定积分的下界
注意这里的上下界的顺序
求多重积分
int()命令可以进行嵌套,即在单重积分的基础上嵌套int命令就可以求多重积分
求数值积分
数值积分是指已知了数值,但是没有关系式
使用命令: trapz(x,y)
例:计算
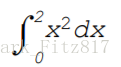
x = linspace(0,2,10); % 将区间[0,2]分成10等份
f = x.^2;
trapz(x,f); % 就得到了积分结果
% 相对于int()求定积分存在一定的误差
求正交积分
使用命令quad()和quadl()都可以,使用方法同int()
美化表达式的显示
命令:pretty(f) 可以将表达式展示成日常手写的形式,方便观察
f: 需要美化的表达式
设置多个图的属性
设置属性的命令是 set(h,key,value)
h 是一个指针,指向图的实例
那么如何获得图的对象呢?
就需要使用 get(gca,'children')命令了
返回的是一个数组,元素是每一个图对象,这样就可以指定每一个图的属性了,比如颜色,线条等