机器学习算法 - 线性回归

线性回归算法

• 解决回归问题
• 思想简单，容易实现
• 许多强大的非线性模型的基础
• 结果具有很好的可解释性
• 蕴含机器学习中很多重要的思想$$y=ax_i +b$$

样本特征只有一个的线性回归问题，为简单线性回归。

样本特征有多个的线性回归问题，为多元线性回归。(由此可见，线性并不代表直线)

线性回归算法将无数的训练集数据放在一个坐标系中，以坐标系的一个维度作为 label，其他维度作为特征， 最终会发现他们是沿着一条直线分布。线性回归算法的最终目的就是寻找出一条直线、一个面或者体 (根据数据的维度而定)， 最大程度上 "拟合" 样本特征和输出 label 之间的关系。

特征是一维时，线性模型在二维空间构成一条直线； 特征是二维时，线性模型在三维空间中构成一个平面； 特征是三维时，则最终模型在四维空间中构成一个体； 以此类推…

简单线性回归算法思想

在简单线性回归中，我们将训练集特征作为横坐标，训练集 label 作为纵坐标，那么我们的最终目的就是 寻找出一条直线 当给出新的特征时， 我们希望能够带入到 中，求出预测值。

公式推导

找到 a 和 b 使得 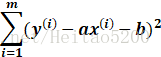尽可能小， 这是一个典型的最小二乘法问题：最小化误差的平方 损失函数是计算期望值和预测值的差值，期望其差值 (也就是损失) 越来越小

简单线性回归算法公式推导

求损失函数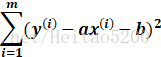 的最小值

最小二乘法求解：本质是试图找到一条直线，使得样本上的点到直线的欧式距离之和最小$$ J(a,b) =  \sum_{i=1}^{m} (y^{(i)} -ax^{(i)} -b)^2 $$

对损失函数求导并且令

$$\frac{\partial J(a,b)}{\partial b}  = 0,\frac{\partial J(a,b)}{\partial a}  = 0$$

$$ \frac{\partial J(a,b)} {\partial b}  =\sum_{i=1}^{m} 2(y^{(i)} -ax^{(i)} -b)(-1)  = 0  \text {} $$