机器学习-线性回归

线性回归
李鹏-南开百度联合实验室

线性回归

基本介绍

假定数据集合中有$m$个样本点，对于每一个样本点$x_i$，具有值$y_i$，且$x = \{x_i | i \in \{0, 1, \ldots, m-1\} \}$与结果$y = \{y_i |i \in \{0, 1, \ldots, m-1\} \}$呈现线性关系。
我们的目标是根据现有的$m$个样本，拟合出一条直线，即

$$y = w * x + b \tag{1}$$
使得根据这条直线得到的结果与真实的结果误差最小。那么如何来衡量这个误差呢？我们引入平方损失函数，即对于样本 $x_i$，我们有误差 $J_i$
$$J_i = (w*x_i+b - y_i)^2$$ 因此，全部 $m$个样本的平均误差为：
$$J = \frac{1}{m}\sum_{i=0}^{m-1}{J_i}$$
从数学上表述为，我们要求得 $w$和 $b$ ，使得 $j$最小，即
$$\arg \min \frac{1}{m}\sum_{i=0}^{m-1}{J_i}$$

针对于最小化特定方程的，我们区分为几个section来介绍。

普通求导

根据多元函数求极值得方法，直接分别对$w$和$b$求偏导，且使得偏导为0，即：

$$\frac{\partial J}{\partial w} = 0, \ \ \ \frac{\partial J}{\partial b} = 0$$
只有两个未知数，两个等式，因此可以解出 $w,b$。

但是，这里面假定了样本点$x_i$只有一列属性，也就是说每一个样本都可以在一个二维图像中描绘出来。当一个样本具有$n$列属性的时候，上述就会有$n+1$个等式，即：

$$\frac{\partial J}{\partial w_0} = 0, \ \ \ldots,\ \ \frac{\partial J}{\partial w_{n-1}} = 0, \ \ \ \frac{\partial J}{\partial b} = 0$$
这样联立线性方程组求解非常复杂.

向量求导

当未特殊说明，向量一律为列向量。
对于具有多个属性的$x_i$，我们拟合的公式$(1)$可以转化为：

$$y = w^T x + b$$
为了统一化，我们将 $w,b$合并为向量 $\theta$，并给 $x_i$增加额外的一个属性，值为1.

这样我们有：

$$y = \theta^T x = x^T \theta$$

此时，平均误差公式可以进一步简化为：

$$\begin{aligned} J(\theta) &= \frac{1}{m} \sum_{i=0}^{m-1}( x_i^T \theta - y_i)^2 \\ &= \frac{1}{m} (X \theta - Y)^T (X \theta - Y)\end{aligned}$$
其中 $X = \begin{bmatrix} x_0^T\\ x_1^T\\ \vdots \\ x_{m-1}^T \end{bmatrix}$，且 $Y= \begin{bmatrix} y_0\\ y_1\\ \vdots\\ y_{m-1} \end{bmatrix}$

我们的目标是求得最小化$J(\theta)$时的 $\theta$值，这可通过向量求导：

$$\tag{2} \frac{\partial J(\theta)} {\partial \theta} = 0$$

为了对公式$(2)$进行求解，我们首先引入几个基本向量求导公式：

$$\begin{aligned} \frac{\partial x^T a}{\partial x} &= \frac{\partial a x^T}{\partial x} = a \\ \frac{\partial x^T B x}{\partial x} &= (B + B^T) x\end{aligned}$$
对于上述的基本求导公式，它的证明只有一个思想：数对向量求导，相当于此数对向量中的各个元素逐个求导。上述的两个公式都是对列向量 $x$求导，因此结果仍然是一个列向量。

上述公式的简单记忆方法： 前导不变，后导转置，公式表达为：

$$\frac{\partial x^T a}{\partial x} = a, \ \ \ \frac{\partial b x}{\partial x} = b^T$$
注意： 这里的 $b$是行向量。

令$Z(\theta) = (X \theta - Y)^T (X \theta - Y)$，
则$J(\theta) = \frac{1}{m}Z(\theta)$，且

$$\begin{aligned} Z(\theta) &= (\theta^T X^T - Y^T) (X \theta - Y) \\ &= \theta^T X^T X \theta - \theta^T X^T Y - Y^T X \theta + Y^TY\end{aligned}$$

因此我们有：

$$\begin{aligned} \frac{\partial {(Z(\theta))}} {\partial \theta} &= (X^TX + X^TX) \theta - X^TY - X^TY + 0 \\ &= 2X^TX \theta - 2 X^T Y \end{aligned}$$

代入$Z(\theta)$到公式$(2)$，我们有：

$$\begin{aligned} \frac{\partial {(\frac{1}{m}Z(\theta))}} {\partial \theta} &= 0 \\ \text{即：} \frac{1}{m}(2X^TX \theta - 2 X^T Y ) &= 0 \\ \text{即：} X^TX \theta - X^T Y &= 0\end{aligned}$$

如果$X^T X$可逆，那么我们有：

$$\theta = (X^TX)^{-1} X^TY$$

上述的优化方法需要计算矩阵的逆，当数据量很小而且可逆的时候，速度快，效果好，但是并不适用于大量高维度的数据。是否有一些数学中的迭代的方式能不断的逼近最小值呢？这个答案有很多，下面将尽力逐个介绍。

梯度下降

梯度下降，顾名思义就是顺着梯度的方向的反方向下滑，直到滑动到某一个最低点为止。
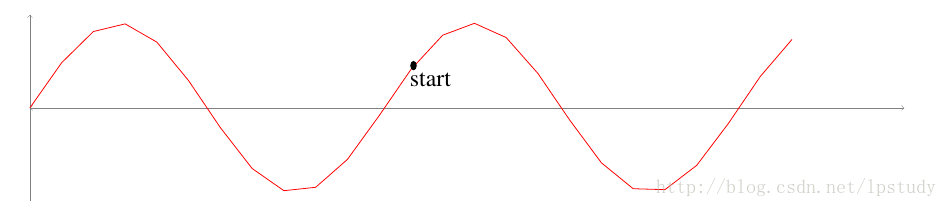
我们可以把它想象成一个小山，如下图所示（
很抱歉是用latex写的，画图采用的tikz，第一次用不熟练，很丑），假定我们的起始点为start，然后顺着下山的方向，一步一步的就会滑落到它左边的最低点。

这可能会有一个问题： 如果它的右边有一个更低的最低点呢？
它有可能落不到全局最低，但是可以达到局部最低。不过，如果我们的函数是凸函数，也就是说只有一个极值点的时候，它的局部最优也就是全局最优了。

梯度下降的“小山”图，从start点开始下落

原理篇

一维直观篇

为了与高等数学教材的保持一致，采用书里面的记法，在$\triangle x \to 0$时，我们有：

$$f(x+ \triangle x) = f(x) + \triangle x \cdot f'(x) + \textit{o}(\triangle x)$$
此后我们简单的忽略 $\textit{o}(\triangle x)$这一项。

令上图中的start点的横坐标为$x_0$，代入$x=x_0$，我们有:

$$f(x_0+ \triangle x) = f(x_0) + \triangle x \cdot f'(x_0)$$

为了使它向着小山下方（左面）滑动，我们需要有$f(x_0 + \triangle x) < f(x_0)$，即

$$\triangle x \cdot f'(x_0) < 0$$

那么$\triangle x$需要满足什么条件呢？我们令$g=f'(x),\ \ \sigma = \triangle x$，我们有：

$$\triangle x \cdot f'(x_0) = g \cdot \sigma$$
很显然，我们只需要 $\sigma$取得 $g$的相反的方向，例如 $\sigma = -0.01g$，即可满足 $g \cdot \sigma < 0$。请原谅我，虽然进行 $g$和 $\sigma$的定义看起来多此一举，但请相信我，当将其映射到高维的时候，它能更好的帮助理解。

负梯度：这里面的$g$是斜率，其实也是梯度。$\sigma$与$g$变化方向相反，因此我们称之为$x$沿着梯度下降的方向，也就是负梯度方向。

学习率：
上面我们说$\sigma$只需要与梯度的方向相反，那么$\sigma = -0.1g, \ \ \sigma = -0.01g$都可以满足要求，因此我们使用变量$\alpha$表达学习率的概念，即$\sigma = -\alpha \cdot g$。

你应该已经知道学习率为何不能太大的原因了吧，上面的描述都是基于$\sigma = \triangle x \to 0$的情况下，进行的推导，在实际中我们通常不会选用太大的$\alpha$，不过太小的$\alpha$意味着学习速度变慢，也就是说需要迭代更多的步数才可以到达最小值。

假定学习率$\alpha = 0.01$，从而我们有迭代公式：

$$x_1 = x_0 -0.01g,\ \ \ \ldots, \ \ \ x_{n+1} = x_n -0.01g$$

利用如上的递推公式，我们就可以不断的使得$f(x_{n+1}) < f(x_n)$，即不断下滑到最低点。

二维梯度篇

我先从二维逐步扩展到高维的形式，二维的微分形式:

$$f(x+\triangle x, y+ \triangle y) = f(x, y) + \triangle x f'(x) + \triangle y f'(y) + \textit{o}(\sqrt{\triangle ^2 x + \triangle^2 y})$$

我们的目标是使得在对于自变量$x, y$进行相应的$\triangle x, \triangle y$变化后，新的$f(x+\triangle x, y+ \triangle y)$能够更小，也就是说使得：

$$\triangle x f'(x) + \triangle y f'(y) + \textit{o}(\sqrt{\triangle ^2 x + \triangle^2 y}) < 0$$

那$\triangle x, \triangle y$需要满足什么条件呢？
我们令$g^T = (f'(x), f'(y) ), \sigma ^T = (\triangle x, \triangle y)$，我们有：

$$\triangle x f'(x) + \triangle y f'(y) = g^T \cdot \sigma = ||g|| \cdot ||\sigma|| \cdot cos(\theta)$$
很显然，我们应该使得 $cos(\theta) = -1$，也就是说 $\sigma$的方向与梯度 $g$的方向相反。

如果加上学习率，我们可以令$\sigma = -\alpha \cdot g$.
同样，与一维的情况一样，也是沿着负梯度的方向。

高维梯度篇

我们终于来到了高维情况，直接利用前面叙述的参数，梯度$g$，学习率$\alpha$，自变量变化$\sigma$，注意$\sigma$是一个向量，它代表各个自变量参数的变化情况，可简单把它想象成$\{\triangle x, \triangle y, \cdots\}$。
我们有：

$$f(X + \sigma) = f(X) + g^T \cdot \sigma + \textit{o}(||\sigma||)$$

同样，我们应该有$\sigma = -\alpha \cdot g$。

梯度下降简单实现demo篇

看到这里，有没有想实现一个梯度下降的冲动，反正我是有的，因此，我用python写了一个非常非常基本的二维的梯度下降，来实现线性回归。

请稍微回到我们在section 1.1中介绍的平面图上的m个点$(x_i, y_i)$，且呈现线性关系，我们的平均误差方程为：

$$J(w,b) = \frac{1}{m}\sum_{i=0}^{m-1}{J_i}$$
其中 $J_i(w,b) = (w*x_i+b - y_i)^2$。我们的目标是解出 $w,b$以使得 $J$最小。

梯度下降的4个要素：

1. 初始值

   $$w_0=0, b_0=0$$

2. 学习率

   $$\alpha = 0.01 \to 0.0001$$

3. 梯度

   $$\begin{aligned} \frac{\partial J(w,b)} {\partial w} &= \frac{1}{m} \sum_{i=0}^{m-1} {2(wx_i+b-y_i)x_i} \\ \frac{\partial J(w,b)} {\partial b} &= \frac{1}{m} \sum_{i=0}^{m-1} {2(wx_i+b-y_i)} \end{aligned}$$

4. 梯度更新

   $$\begin{aligned} w_{n+1} &= w_{n} - \alpha \cdot \frac{\partial J(w,b)} {\partial w} \\ b_{n+1} &= b_{n} - \alpha \cdot \frac{\partial J(w,b)} {\partial b} \end{aligned}$$

我们使用的数据点如下面的散点图所示，它是使用$w=2, b=3$的公式在$x \in \{0, 1, \ldots, 99 \}$中加入一定的随机数得到的。

线性回归之梯度下降数据分布图

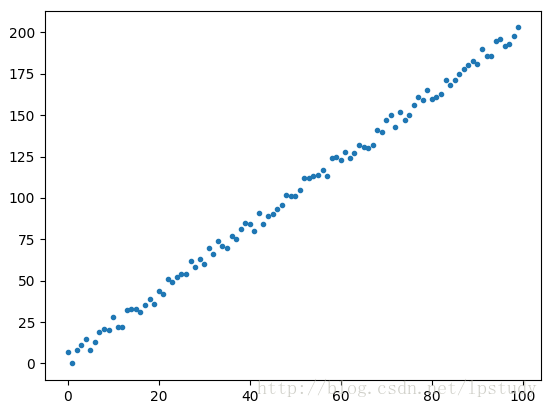
生出散点图的python代码如下

import numpy as np
import random
import matplotlib.pyplot as plt
import pdb

random.seed(10)
x = np.arange(100)
w, b = 2, 3
y = np.array([w * i + b + random.randint(-5,5) for i in x])
one = np.ones(len(x))
plt.plot(x, y, '.')
plt.show()

利用梯度下降的4个要素编写的代码如下：

#alpha and g
alpha = 0.0003
w0, b0 = 0, 0

def gradient_w(w, b):
    return np.average([2*(w*xi + b - yi)* xi for (xi, yi) in list(zip(x,y))])
def gradient_b(w, b):
    return np.average([2*(w*xi + b - yi) for (xi, yi) in list(zip(x,y))])

for i in range(100000):
    w1 = w0 - alpha * gradient_w(w0, b0)
    b1 = b0 - alpha * gradient_b(w0, b0)
    w0, b0 = w1, b1
plt.plot(x, y, 'k+')
plt.plot(x, w0 * x + b0, 'r')
plt.show()

最终迭代出的结果为： $w1 = 1.99700571226 b1 = 3.19821704612$

画出的曲线如下图所示

线性回归之梯度下降曲线结果

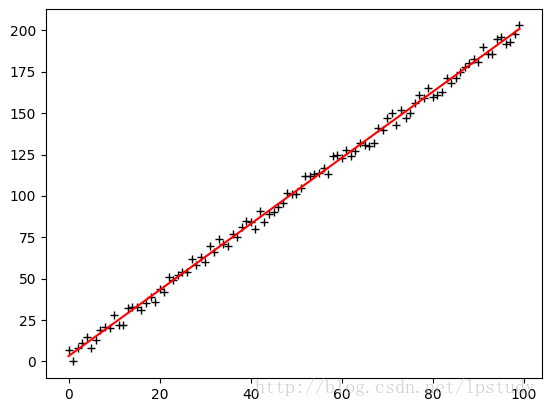
代码其实几分钟就写完了，但是一直都拟合不出来，当时我设置的学习率为$alpha=0.001$，还没有迭代多少步，就出现了值无穷大(nan)的情况，我一直以为是代码有问题，检查了一遍又一遍，还是感觉代码没问题，后来直到调整了学习率之后，才能够正确拟合出结果。

学习率的影响：
学习率过小，导致学习速度过慢，如果设置了最大迭代次数，那么很有可能还没有学到最终结果的时候，就已经终止了。不过我们可以看到它的误差，即$J(w,b)$是呈现一个不断下降的趋势。
学习率过大，虽然学习速度上去了，但是很有可能跳出了最优解，这可能会导致算法最终并不会收敛，误差通常会溢出。

我从网上盗取了两张图，来分别展示学习率大小对结果的影响。

线性回归之梯度下降不同学习率小（左）和大（右）的情况

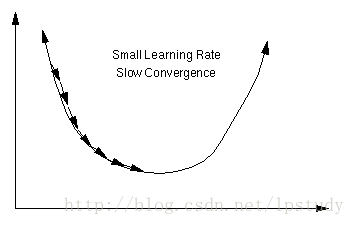
对于学习率引起的问题，我给上述的梯度下降代码加入了误差计算并存储，并画出误差图。

线性回归之梯度下降不同学习率小（左）和大（右）的误差情况

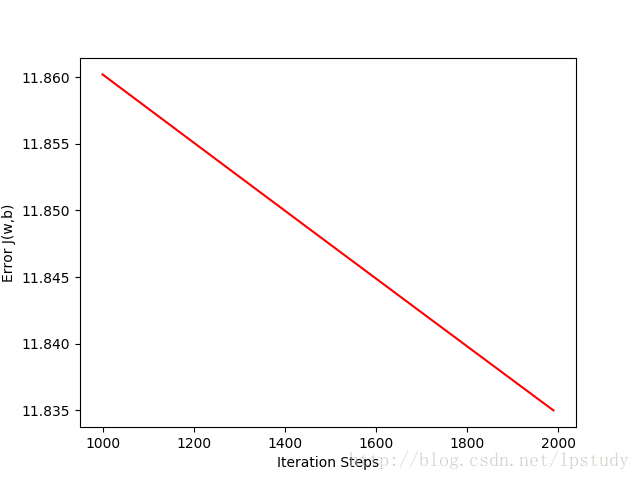
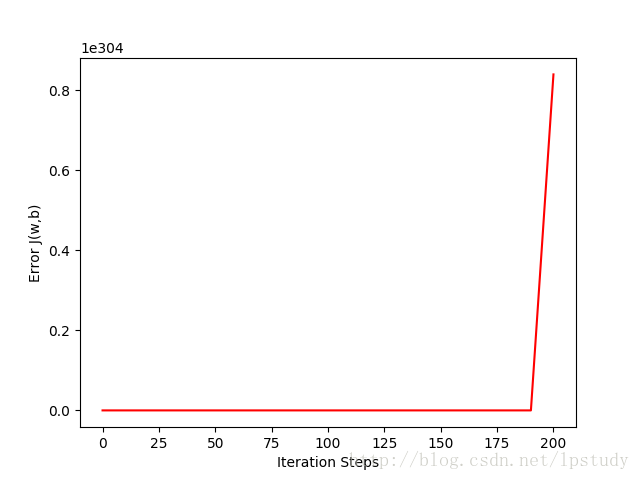
在使用学习率$\alpha = 0.00001$，迭代2000次后，我们得到$w1 = 2.04427897398,\ b1 = 0.0626663170812$，可以看出这与实际的$w=2, b=3$还是有不小的差距的，其误差画出曲线如误差图中的左图所示。
在使用学习率$\alpha = 0.001$，迭代2000次后，我们得到$w1 = nan, b1 = nan, error = nan$，它的误差如误差图的右图所示。

根据误差图，就可以很容易指导我们是学习率不够，迭代次数不够，还是学习率过大。当误差依然处于下降的趋势，我们的迭代次数通常是不够的，如果时间不允许，那么可以稍微调整学习率，使用更大的学习率来加快收敛，但是不能过大，以免出现误差不收敛。

牛顿法

牛顿法与梯度下降法具有很大的相似性，区别在于梯度下降是采用的一阶导数，而牛顿法采用的二阶导数。

一维直观篇

请拿上我们的高等数学中的泰勒展开，采用书里面的记法，在$\triangle x \to 0$时，我们有：

$$f(x+\triangle x) = f(x) + \triangle x \cdot f'(x) + \frac{1}{2}\triangle^2 x \cdot f''(x) + \textit{o}(\triangle^2 x)$$

同样的，我们需要求得这样的$\triangle x$，以使得$f(x+\triangle x)$尽可能的小。回顾在梯度下降中，我们只是将泰勒展开到前面的两项，然后得到$\triangle x = -\alpha \cdot f'(x)$可以使得$f(x+\triangle x)$呈现下降趋势，即沿着负梯度的方向。

在牛顿法中，我们的泰勒展开到了$\triangle x$的平方项，这使得我们可以换个思路以最小化$f(x+\triangle x)$：将$\triangle x$当成未知量，公式$f(x) + \triangle x \cdot f'(x) + \frac{1}{2}\triangle^2 x \cdot f''(x)$是一个一元二次方程，曲线的开口向上，因此我们有$\triangle x = -\frac{f'(x)}{f''(x)}$使得$f(x+\triangle x)$取得最小值。
它与梯度下降很大的不同在于梯度下降的$\triangle x$只要求方向与梯度方向相反即可，而牛顿法却可以精确的求出$\triangle x$的值。

高维原理篇

假定有n个自变量参数$\{x_1, x_2, \ldots, x_n\}$，，自变量变化$\sigma$，注意$\sigma$是一个向量，它代表各个自变量参数的变化情况，可简单把它想象成$\{\triangle x_1, \triangle x_2, \cdots\}$，这里我们还需要额外的一个$G$，它表示对自变量的二阶导数。

我们有学习率$\alpha$(这是一个数)，梯度向量$g$:

$$g = \begin{bmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \\ \vdots\\ \frac{\partial f}{\partial x_n} \end{bmatrix}$$ 自变量的变化 $\sigma$: $$\sigma = \begin{bmatrix} \triangle x_1\\ \triangle x_2\\ \vdots \\ \triangle x_n \end{bmatrix}$$ 二阶导数矩阵hessian矩阵 $G$： $$G = \begin{bmatrix} \frac{\partial^2 f}{\partial x_1^2},\ \frac{\partial^2 f}{\partial x_1 \partial x_2}, \ldots, \frac{\partial^2 f}{\partial x_1 \partial x_n}\\ \frac{\partial^2 f}{\partial x_2 \partial x_1}, \frac{\partial^2 f}{\partial x_2^2}, \ldots, \frac{\partial^2 f}{\partial x_2 \partial x_n}\\ \vdots\\ \frac{\partial^2 f}{\partial x_n \partial x_1}, \frac{\partial^2 f}{\partial x_n \partial x_2}, \ldots, \frac{\partial^2 f}{ \partial x_n^2} \end{bmatrix}$$ 可以看出 $G$是对称矩阵，即 $G = G^T$。

我们有：

$$f(X + \sigma) = f(X) + g^T \cdot \sigma + \frac{1}{2}\sigma^T \cdot G \cdot \sigma + \textit{o}(||\sigma||^2)$$

利用前面学到的向量求导公式，对$\sigma$求导，使得导数为0，即

$$\begin{aligned} \frac{\partial f(X+\sigma)}{\partial \sigma} &= g + \frac{1}{2}(G+G^T) \cdot \sigma \\ &= g+G \cdot \sigma \\ &= 0\end{aligned}$$ 因此，我们有: $$\sigma = - G^{-1} \cdot g$$
然后我们就可以利用得到的 $\sigma$，得到新的 $X_{new} = X + \sigma$，进行下一步迭代。

牛顿法代码Demo篇

计算$g$和$G$的代码：

def gradient_w(w, b):
    return np.average([2*(w*xi + b - yi)* xi for (xi, yi) in list(zip(x,y))])
def gradient_b(w, b):
    return np.average([2*(w*xi + b - yi) for (xi, yi) in list(zip(x,y))])

def gradient_w_w(w, b):
    return np.average([2 * xi * xi for (xi, yi) in list(zip(x, y))])
def gradient_w_b(w, b):
    return np.average([2 * xi for (xi, yi) in list(zip(x, y))])
def gradient_b_w(w, b):
    return np.average([2 * xi for (xi, yi) in list(zip(x,y))])
def gradient_b_b(w, b):
    return np.average([2 for (xi, yi) in list(zip(x,y))])
def error(w, b):
    return np.average([np.square(w*xi + b - yi) for (xi, yi) in list(zip(x,y))])

牛顿迭代的代码：

erros = [[], []]
for i in range(2000):
    g = np.mat([gradient_w(w0, b0), gradient_b(w0, b0)]).T
    G = np.mat([[gradient_w_w(w0, b0), gradient_w_b(w0, b0)], [gradient_b_w(w0, b0), gradient_b_b(w0, b0)]])

    sigma = -G.I * g
    w1 = w0 + sigma[0, 0]
    b1 = b0 + sigma[1, 0]

    erros[0].append(i)  
    erros[1].append(error(w1, b1))
    w0, b0 = w1, b1

plt.plot(x, y, 'k+')
plt.plot(x, w0 * x + b0, 'r')
plt.show()

从误差结果看，它一次迭代就可以得到最小值，后经过@景宽提醒，牛顿法本身计算的就是二阶泰勒展开的值。我们上述的直线方程只有两个系数，它的三阶泰勒值就是0，因此二阶泰勒展开就是它的最小值了。

最小二乘法的最大似然解释

前面在Section基本介绍中，我们直接用平方损失函数来最小化来得到最优直线。那么，你是否有疑问，为什么平方损失函数最小就可以得到最优的直线，而不是绝对值损失，或者四次方损失呢？

这其实涉及到概率论中的最大似然估计.
上述的问题，可以转化为：对于$m$个点形成的集合$D = \{d1, d2, \ldots, d_m\}$，我们需要拟合一条直线$h$，以使得拟合的直线最切合这个数据集合$D$，也就是说我们要最大化概率$P(h|D)$。

由贝叶斯公式

$$\begin{aligned} P(h | D) &= \frac{P(D|h) \cdot P(h)}{P(D)} \propto P(D|h)\end{aligned}$$
如果各个点相互独立，则
$$P(h|D) \propto P(d_1|h) \cdot P(d_2|h) \cdot \ldots \cdot P(d_n |h)$$

对于$P(d_i |h)$表示的是在给定直线$h$的情况下，具有点$d_i$的概率。我们假设各个点的误差$\triangle y_i = \overline{y_i}-y_i$服从均值为0，方差为$\sigma$的正态分布，也就是说，在给定直线$h$的情况下，点$d_i$出现的概率为服从：

$$P(d_i | h) \propto e^{-\frac{\triangle^2 y_i}{2 \sigma^2}}$$

于是，我们有:

$$P(h|D) \propto e^{\sum_{i=1}^{m}(-\frac{\triangle^2 y_i}{2 \sigma^2})}$$

从而最大化$P(h|D)$，等价于最小化$\sum_{i=1}^{m}(\triangle^2 y_i)$，也就是前面说的最小化平方误差。

另一种说法：
对于样本点$d_i$，对样本点的预测取决于参数$\theta$的选取，且我们有

$$\triangle y_i = \overline{y_i} -y_i$$
其中 $\overline{y_i}$是 $y_i$的预测值， $y_i$为真实值， $\triangle y_i$为误差。

一般我们认为误差服从正态分布，即

$$\begin{aligned} \triangle y_i \sim \textit{N}(0, \sigma)\end{aligned}$$
现在我们需要选取 $\theta$，以使得取得 $y_i$的概率最大，即
$$L(\theta) = \prod_{i=1}^{m} P(y_i | \theta) = \prod_{i=1}^m\frac{1}{\sqrt{2\pi}\sigma}\exp(-\frac{\triangle ^2 y_i}{2\sigma})$$
两边取 $log$，乘积变求和，因此同样转换为最小化 $\sum_{i=1}^{m}(\triangle^2 y_i)$，也就是前面说的最小化平方误差。

参考文献：

https://www.cnblogs.com/21207-iHome/p/5222993.html

http://blog.csdn.net/ying_xu/article/details/51240291

https://www.cnblogs.com/happylion/p/4172632.html

http://blog.csdn.net/lydyangliu/article/details/9208635

http://www.fuzihao.org/blog/2014/06/13/为什么最小二乘法对误差的估计要用平方/

https://www.zhihu.com/question/20447622