【机器学习算法总结】线性回归

1 机器学习概念

• 损失函数/代价函数：当我们选定决策函数 $f(X)$时，对于给定的输入 $X$，由 $f(X)$给出相应的输出 $Y$，为了能够表现出 $f(X)$拟合的好坏，我们定义一个函数来度量拟合的程度，这个函数就称为损失函数。比如 $L ( Y , f ( X ) ) = ( Y - f ( X ) ) ^ { 2 }$
• 过拟合：如果一味提高模型对训练数据的预测能力时，模型的复杂度会提高，此时对于测试数据的预测能力就会降低。
• 正则化：解决过拟合的典型方法就是正则化，在损失函数上加一个正则化项，一般为模型参数向量的范数，他的作用是选择损失函数和正则化项同时较小的模型参数。
• 目标函数：目标函数即最终优化的函数，与损失函数有关，在加上正则化项之后，最终的目标函数及为 $\min ( Y - f ( X ) ) ^ { 2 } + \lambda J ( f )$
• 泛化能力：泛化能力是指模型对未知数据的预测能力，一般采用测试数据集的误差来评价模型的泛化能力。
• 评价函数：模型的评价一般基于训练误差和测试误差，另外在分类问题中，也会用精确率，召回率和F1score等来评价模型的好坏。

2 线性回归

假设有数据集 $D = \left\{ \left( x _ { 1 } , y _ { 1 } \right) , \left( x _ { 2 } , y _ { 2 } \right) , \cdots , \left( x _ { m} , y _ { m } \right) \right\}$。
当 $x_i$有且仅有一个特征时，便可以构建出线性回归模型： $f ( x ) = \theta _ { 0 } + \theta _ { 1 } x_i$，其中 $\theta$即为要学习的参数。
当 $x_i$有n个特征时，即 $x_i = (x_i^1,x_i^2,x_i^3, \cdots,x_i^n)$，令 $x_i = (1,x_i^1,x_i^2,x_i^3, \cdots,x_i^n)$， $\theta = (\theta_0,\theta_1,\theta_2,\theta_3, \cdots,\theta_j,\cdots,\theta_n)$。则线性回归模型为： $f ( x_i ) = \theta ^T x_i$。
然后将数据集进行向量化，其中 $X=(x_1,x_2,x_3,\cdots,x_m)^T，\theta = (\theta_0,\theta_1,\theta_2,\theta_3, \cdots,\theta_n)^T$，则 $f ( X ) = X \theta$

3 代价函数

线性回归的目标就是选择出可以使得整个训练集的预测误差最小的模型参数，评价这一误差的函数就是代价函数(cost function)，整个训练过程就是让代价函数趋于最小值，这里总结两种代价函数：均方误差(MSE)和平均绝对误差(MAE)。一般来说，均方误差更为常用。 $MSE：\quad J ( \theta ) = \frac { 1 } { 2 m } \sum _ { i = 1 } ^ { m } \left( f \left( x _ { i } \right) - y _ { i } \right) ^ { 2 }=\frac { 1 } { 2 m } (X \theta -y) ^T (X \theta -y)$ $MAE：J ( \theta ) = \frac { 1 } { 2 m } \sum _ { i = 1 } ^ { m } \left| f \left( x _ { i } \right) - y _ { i } \right|=\frac { 1 } { 2 m } \sum |X \theta -y|$

4 代价函数求解

4.1 正规方程求解

要求得代价函数得最小值点，我们只需要通过求 $\frac { \partial } { \partial \theta } L \left( \theta \right) = 0$即可，这种方法就是正规方程求解。利用正规方程进行求解，可以得到 $\theta = \left( X ^ { T } X \right) ^ { - 1 } X ^ { T } y$，下面是求解方法。 $J ( \theta ) = \frac { 1 } { 2 } ( X \theta - y ) ^ { 2 }= \frac { 1 } { 2 } ( X \theta - y ) ^ { T } ( X \theta - y )= \frac { 1 } { 2 } \left( \theta ^ { T } X ^ { T } X \theta - \theta ^ { T } X ^ { T } y - y ^ { T } X \theta - y ^ { T } y \right)$ $\frac { \partial J ( \theta ) } { \partial \theta } = \frac { 1 } { 2 } \left( 2 X ^ { T } X \theta - X ^ { T } y - X ^ { T } y - 0 \right)= X ^ { T } X \theta - X ^ { T } y$综上，当 $\frac { \partial J ( \theta ) } { \partial \theta } = 0$时，求得 $\theta = \left( X ^ { T } X \right) ^ { - 1 } X ^ { T } y$。

但是目前常用的优化方法为梯度下降法，因为正规方程方法在使用得时候有以下限制，

• 当矩阵X不可逆时，正规方程方法是不能用的。比如当X中的特征之间不独立，或者特征数量n+1大于训练集的数量m
• 当特征数量比较大时，最好使用梯度下降方法，因为正规方程随特征数量增大，计算复杂度也比较大，一般这个值选择在10000
• 正规方程只适用于线性模型，不适用于逻辑回归或其他模型。

4.2 梯度下降法

梯度下降法的优化思想是用当前位置的负梯度方向作为搜索方向，沿着这个方向寻找最小值。基本过程：首先定 $\theta$的初始位置，然后通过代价函数的梯度不断改变 $\theta$，最后求得代价函数的最小值。更新方法如下，其中 $\alpha$为学习率： $\theta _ { j } : = \theta _ { j } - \alpha \frac { \partial } { \partial \theta _ { j } }J ( \theta )$

4.2.1 批量梯度下降(BGD)

批量梯度下降得到的是一个全局最优解，每迭代一步，都会用到训练集所有的数据，如果m很大，那么可想而知这种方法的迭代速度会相当的慢： $\theta _ { j } : = \theta _ { j } - \alpha \frac { \partial } { \partial \theta _ { j } } J ( \theta ) = \theta _ { j } - \alpha \frac { 1 } { m } \sum _ { i = 1 } ^ { m } \left( \left( f \left( x _ { i } \right) - y _ { i } \right) \cdot x ^ { j } _ { i } \right)$
当然，这种方法可以以向量化的方式实现，一定程度上也可以加快优化的速度： $\theta : = \theta - \alpha \frac { 1 } { m } \left( X ^ { T } ( X \theta - y ) \right)$

4.2.2 随机梯度下降(SGD)

与BGD不同的是，随机梯度下降参数的更新只用到某一个样本，而不是全部的样本，批量梯度下降公式中的m变为了1。但是这种方法的每次迭代并不是朝着总体最优的方向前进，最终也难以达到全局最优，而仅仅在最优点附近。 $\theta _ { j } : = \theta _ { j } - \alpha \left( f \left( x _ { i } \right) - y _ { i } \right) \cdot x ^ { j } _ { i }$

5 sklearn实例

sklearn.linear_model.LinearRegression

参数	类型/默认	解释
fit_intercept	bool/True	是否计算截距，False表示不使用截距
normalize	bool/False	若fit_intercept为False，忽略此参数；如果True，则会首先对数据进行标准化
copy_X	bool/True	如果为True，x将被复制；否则被重写
n_jobs	int/1	计算时设置的进程个数

sklearn.linear_model.SGDRegressor

参数	类型/默认	解释
loss	str/ ‘squared_loss’	损失函数：‘squared_loss’, ‘huber’, ‘epsilon_insensitive’, ‘squared_epsilon_insensitive’
penalty	str/ ‘l2’	正则化项，一般为‘l2’, ‘l1’；‘elasticnet’为两者的混合项，由参数‘l1_ratio ’确定
alpha	float/0.0001	正则化项系数，当learning_rate =‘optimal’时也用来计算学习率
max_iter	int/	最大迭代次数
tol	float / 1e-3	若为None，则max_iter =1000；否则，两次梯度下降的loss之差小鱼tol时停止
learning_rate	string/ ‘invscaling’	学习率，默认参数下等于eta0 / pow(t, power_t)，‘eta0‘，’power_t‘均为参数，t为时间步长

##构建数据集
X = np.random.uniform(-3, 3, 100).reshape(-1, 1)
y = 1.3 * X + 1.1 + np.random.normal(0, 1, 100).reshape(-1, 1)
##构建线性回归
linear_model = LinearRegression()
linear_model.fit(X, y)
y_linear_pred = linear_model.predict(X)
print(linear_model.score(X, y))#0.8359
##梯度下降
sgd_model = SGDRegressor()
sgd_model.fit(X, y)
y_sgd_pred = sgd_model.predict(X)
print(sgd_model.score(X, y))#0.8179
##画出数据集及拟合的模型
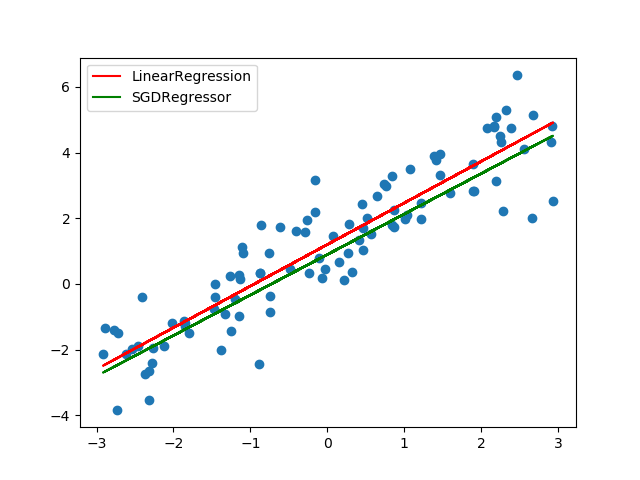
plt.scatter(X, y)
plt.plot(X, y_linear_pred, 'r-', label='LinearRegression')
plt.plot(X, y_sgd_pred, 'g-', label='SGDRegressor')
plt.legend()

参考

1. 统计学习方法
2. 机器学习_吴恩达
3. 常见的几种优化方法
4. sklearn.linear_model