多视几何：摄像机模型的推导

标签（空格分隔）：计算机视觉·多视几何

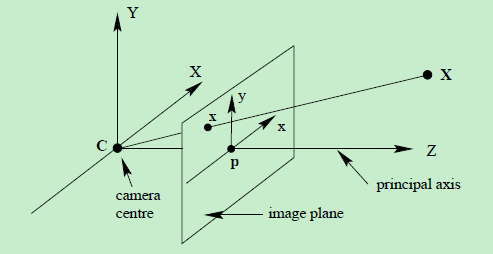
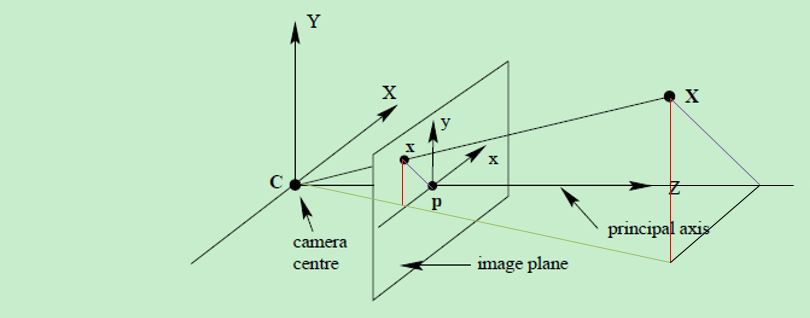
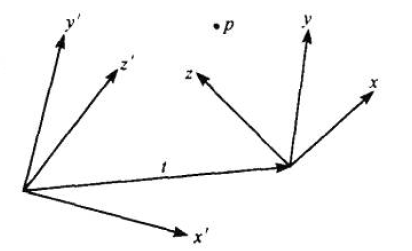
摄像机的作用是将3D空间点 $X$ 映射到2D图像点 $x$ ，而摄像机模型正是对应这个变换的矩阵P；

摄像机模型的推导分为两个步骤: 摄像机坐标系下的点投影到图像平面–>世界坐标系下的点投影到图像平面

多视几何摄像机模型的推导
摄像机坐标系下的点投影到图像平面
- 1 图像坐标系原点位于图像中心
- 2 图像坐标系原点移动到图像左下角
世界坐标系下的点投影到图像平面
关于R和t的几何意义
刚体变换
欧拉角Euler angles
四元数unit quaternions

注：这里提到的摄像机都是针孔摄像机模型！

1. 摄像机坐标系下的点投影到图像平面

有一个空间点 $\mathbf{X}$ ，它在摄像机坐标系下的坐标为 $(X,Y,Z)^T$ ，即

$X = (X, Y, Z) T$ $\mathbf{X} = (X,Y,Z)^T$
那么，它在图像平面中的投影点x是什么？

这里写图片描述

1.1 图像坐标系原点位于图像中心

这里写图片描述

根据相似三角形，可以得到如下两式

$x X = f Z 和 y Y = f Z$ $\frac{x}{X} = \frac{f}{Z} 和 \frac{y}{Y} = \frac{f}{Z}$
从而，有

$x = X Z f 和 y = Y Z f$ $x = \frac{X}{Z}f 和y = \frac{Y}{Z}f$
也就是说，空间中的点 $(X,Y,Z)$ 被映射成为 $(x,y)^T = (\frac{X}{Z}f,\frac{Y}{Z}f)^T$
对上式进行变形，可以得到
$(Z x, Z y) T = (X f, Y f) T$ $(Zx,Zy)^T = (Xf,Yf)^T$
也就是
$(Z x, Z y, Z) T = (X f, Y f, Z) T$ $(Zx,Zy,Z)^T = (Xf,Yf,Z)^T$
记为齐次坐标的形式
$Z (x, y, 1) T = (X f, Y f, Z) T = ⎡ ⎣ ⎢ f 00 0 f 0 001000 ⎤ ⎦ ⎥ (X, Y, Z, 1) T$ $Z(x,y,1)^T = (Xf,Yf,Z)^T=\begin{bmatrix} f & 0&0 &0\\ 0 & f &0&0 \\ 0 & 0 &1 &0 \end{bmatrix}(X,Y,Z,1)^T$
即
$Z (x, y, 1) T = ⎡ ⎣ ⎢ f 00 0 f 0 001000 ⎤ ⎦ ⎥ (X, Y, Z, 1) T$ $Z(x,y,1)^T = \begin{bmatrix} f & 0&0 &0\\ 0 & f &0&0 \\ 0 & 0 &1 &0 \end{bmatrix}(X,Y,Z,1)^T$

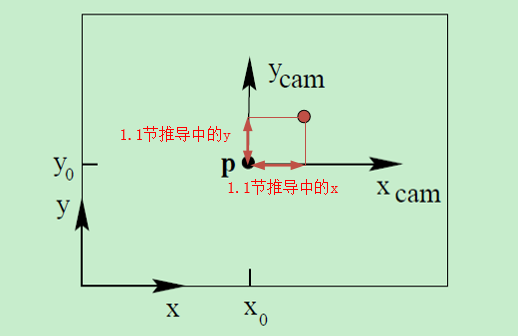
1.2 图像坐标系原点移动到图像左下角

这里写图片描述

此变化对上面的推导有一个影响：上面推导的 $(x,y)$ 应该变为 $(x-x_0,y-y_0)$ ，从而，最后的结果发生如下变化

$x = X Z f + x 0 和 y = Y Z f + y 0$ $x = \frac{X}{Z}f + x_0和y = \frac{Y}{Z}f+ y_0$
$Z x = X f + Z x 0 和 Z y = Y f + Z y 0$ $Zx = Xf + Zx_0和Zy = Yf+Z y_0$
$(Z x, Z y, Z) T = (X f + Z x 0, Y f + Z y 0, Z) T$ $(Zx,Zy,Z)^T = (Xf + Zx_0,Yf+Z y_0,Z)^T$
$Z (x, y, 1) T = (X f + Z x 0, Y f + Z y 0, Z) T = ⎡ ⎣ ⎢ f 00 0 f 0 x 0 y 0 1 000 ⎤ ⎦ ⎥ (X, Y, Z, 1) T$ $Z(x,y,1)^T = (Xf + Zx_0,Yf+Z y_0,Z)^T=\begin{bmatrix} f & 0&x_0 &0\\ 0 & f &y_0&0 \\ 0 & 0 &1 &0 \end{bmatrix}(X,Y,Z,1)^T$
即

$Z ⎛ ⎝ ⎜ x y 1 ⎞ ⎠ ⎟ = ⎡ ⎣ ⎢ f 00 0 f 0 x 0 y 0 1 000 ⎤ ⎦ ⎥ ⎛ ⎝ ⎜ ⎜ ⎜ X Y Z 1 ⎞ ⎠ ⎟ ⎟ ⎟$ $Z \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{bmatrix} f & 0&x_0 &0\\ 0 & f &y_0&0 \\ 0 & 0 &1 &0 \end{bmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix}$

2. 世界坐标系下的点投影到图像平面

上面讨论的问题是：摄像机坐标系下的点投影到图像平面，但实际中，需要的是坐标系下的点投影到图像平面，所以，还需要将上面的摄像机坐标系下的点表示为世界坐标系下，空间点在摄像机坐标系的坐标记为 $X_{cam}$ ，在世界坐标系下的坐标记为 $X$ ；上一小节中的 $(X,Y,Z)$ 其实应该是 $(X_{cam},Y_{cam},Z_{cam})$ (为了方便，便没写该下标)，即

$Z c a m ⎛ ⎝ ⎜ x y 1 ⎞ ⎠ ⎟ = ⎡ ⎣ ⎢ f 00 0 f 0 x 0 y 0 1 000 ⎤ ⎦ ⎥ ⎛ ⎝ ⎜ ⎜ ⎜ X c a m Y c a m Z c a m 1 ⎞ ⎠ ⎟ ⎟ ⎟$ $Z_{cam} \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{bmatrix} f & 0&x_0 &0\\ 0 & f &y_0&0 \\ 0 & 0 &1 &0 \end{bmatrix} \begin{pmatrix} X_{cam}\\ Y_{cam}\\ Z_{cam}\\ 1 \end{pmatrix}$

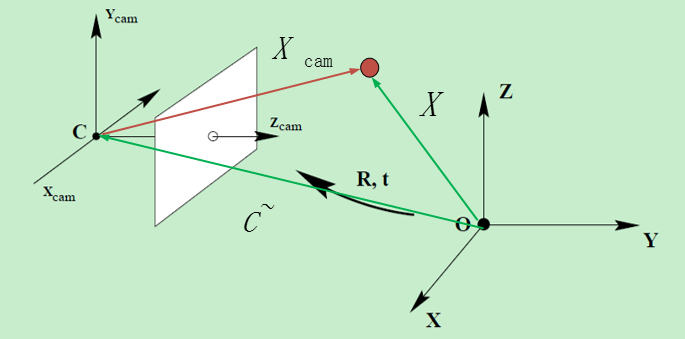
摄像机坐标系和世界坐标系之间存在一个旋转和平移的关系，旋转关系利用旋转矩阵 $R=(r_1,r_2,r_3)$ 表示，平移关系利用平移向量 $t=-R\widetilde{C}$ 表示，其中， $\widetilde{C}$ 为摄像机的光心在世界坐标系下的非齐次坐标

这里写图片描述

下面推导世界坐标系下的点的坐标 $X$ 和摄像机坐标系下的点的坐标 $X_{cam}$ 之间的关系
- 考虑世界坐标系下：
  - 向量 $X$ 在世界坐标系下的方向向量为 $X$
  - 摄像机的光心 $C$ 在世界坐标系下的方向向量为 $\widetilde{C}$
  - 那么，向量 $X_{cam}$ 在世界坐标系下的方向向量为 $X-\widetilde{C}$
- 接下来考虑摄像机坐标系，由于世界坐标系经过旋转矩阵R可以旋转到摄像机坐标，向量 $X_{cam}$ 在摄像机坐标系下的方向为 $R(X-\widetilde{C})$ ，即
  $X c a m = R (X - C ˜)$ $X_{cam} = R(X-\widetilde{C})$
- 将上式写为分量形式（非齐次形式）
  
  $⎛ ⎝ ⎜ X c a m Y c a m Z c a m ⎞ ⎠ ⎟ = R ⎛ ⎝ ⎜ X Y Z ⎞ ⎠ ⎟ - R C ˜ = R ⎛ ⎝ ⎜ X Y Z ⎞ ⎠ ⎟ + t$ $\begin{pmatrix} X_{cam}\\ Y_{cam}\\ Z_{cam} \end{pmatrix}=R \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} -R\widetilde{C}=R \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} +t$
- 写为齐次形式
  
  $X c a m = R (X - C ˜)$ $X_{cam} = R(X-\widetilde{C})$
- 将上式写为分量形式（非齐次形式）
  $⎛ ⎝ ⎜ ⎜ ⎜ X c a m Y c a m Z c a m 1 ⎞ ⎠ ⎟ ⎟ ⎟ = ⎛ ⎝ ⎜ ⎜ ⎜ R ⎛ ⎝ ⎜ X Y Z ⎞ ⎠ ⎟ 1 ⎞ ⎠ ⎟ ⎟ ⎟ + (t 1) = (R 0 T t 1) ⎛ ⎝ ⎜ ⎜ ⎜ X Y Z 1 ⎞ ⎠ ⎟ ⎟ ⎟$ $\begin{pmatrix} X_{cam}\\ Y_{cam}\\ Z_{cam}\\ 1 \end{pmatrix}= \begin{pmatrix} R \begin{pmatrix} X\\ Y\\ Z \end{pmatrix}\\ 1 \end{pmatrix} +\begin{pmatrix} t\\ 1 \end{pmatrix} =\begin{pmatrix} R & t\\ 0^T & 1 \end{pmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix}$
  其中
  $(R 0 T t 1) = ⎛ ⎝ ⎜ ⎜ ⎜ r 11 r 21 r 31 0 r 12 r 22 r 32 0 r 13 r 23 r 33 0 t 1 t 2 t 3 1 ⎞ ⎠ ⎟ ⎟ ⎟$ $\begin{pmatrix} R & t\\ 0^T & 1 \end{pmatrix} = \begin{pmatrix} r_{11} &r_{12} &r_{13} & t_1\\ r_{21}& r_{22} &r_{23} &t_2 \\ r_{31} & r_{32} & r_{33} & t_3\\ 0 & 0 &0 &1 \end{pmatrix}$
上面得到了空间点在世界坐标系下的坐标和摄像机坐标系下的坐标之间的关系，结合摄像机坐标系与图像坐标系的关系，可以得到摄像机模型

$⎛ ⎝ ⎜ ⎜ ⎜ X c a m Y c a m Z c a m 1 ⎞ ⎠ ⎟ ⎟ ⎟ = (R 0 T t 1) ⎛ ⎝ ⎜ ⎜ ⎜ X Y Z 1 ⎞ ⎠ ⎟ ⎟ ⎟$ $\begin{pmatrix} X_{cam}\\ Y_{cam}\\ Z_{cam}\\ 1 \end{pmatrix}=\begin{pmatrix} R & t\\ 0^T & 1 \end{pmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix}$

Z c a m ⎛ ⎝ ⎜ x y 1 ⎞ ⎠ ⎟ = ⎡ ⎣ ⎢ f 00 0 f 0 x 0 y 0 1 000 ⎤ ⎦ ⎥ ⎛ ⎝ ⎜ ⎜ ⎜ X c a m Y c a m Z c a m 1 ⎞ ⎠ ⎟ ⎟ ⎟

$Z_{cam} \begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{bmatrix} f & 0&x_0 &0\\ 0 & f &y_0&0 \\ 0 & 0 &1 &0 \end{bmatrix} \begin{pmatrix} X_{cam}\\ Y_{cam}\\ Z_{cam}\\ 1 \end{pmatrix}$

Z c a m ⎛ ⎝ ⎜ x y 1 ⎞ ⎠ ⎟ = ⎡ ⎣ ⎢ f 00 0 f 0 x 0 y 0 1 000 ⎤ ⎦ ⎥ (R 0 T t 1) ⎛ ⎝ ⎜ ⎜ ⎜ X Y Z 1 ⎞ ⎠ ⎟ ⎟ ⎟

$Z_{cam}\begin{pmatrix} x\\ y\\ 1 \end{pmatrix} = \begin{bmatrix} f & 0&x_0 &0\\ 0 & f &y_0&0 \\ 0 & 0 &1 &0 \end{bmatrix} \begin{pmatrix} R & t\\ 0^T & 1 \end{pmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix}$

即得到了摄像机模型
$x = [K R K t] X = K [R t] X = K R [I | - C ˜]$ $x = \begin{bmatrix} KR & Kt \end{bmatrix}X = K\begin{bmatrix} R & t \end{bmatrix}X = KR[I |-\widetilde{C}]$

这里写图片描述

如果需要将图像坐标表示为像素形式，该如何转换呢？

上面的空间点对应的图像坐标(x,y)是物理长度坐标，现在需要将其转换为像素坐标，那么，假设在图像平面内，x、y方向上单位距离内的像素个数分别为 $m_x$ 和 $m_y$ ，从而，空间点对应的图像坐标若以像素为单位，则可以表示为

$u = x * m x, v = y * m y$ $u = x*m_x, v = y*m_y$
另外， $f_x$ 、 $f_y$ 和 $x_0$ 、 $y_0$ 对应的像素值分别为
$a x = f x * m x, a y = f y * m y$ $a_x = f_x * m_x, a_y = f_y * m_y$
$p x = x 0 * m x, p y = y 0 * m y$ $p_x = x_0 * m_x, p_y = y_0 * m_y$
从而，计算机模型可以表示为
$Z c a m ⎛ ⎝ ⎜ u v 1 ⎞ ⎠ ⎟ = ⎡ ⎣ ⎢ f x 00 0 f y 0 x 0 y 0 1 000 ⎤ ⎦ ⎥ (R 0 T t 1) ⎛ ⎝ ⎜ ⎜ ⎜ X Y Z 1 ⎞ ⎠ ⎟ ⎟ ⎟$ $Z_{cam}\begin{pmatrix} u\\ v\\ 1 \end{pmatrix} = \begin{bmatrix} f_x & 0&x_0 &0\\ 0 & f_y &y_0&0 \\ 0 & 0 &1 &0 \end{bmatrix} \begin{pmatrix} R & t\\ 0^T & 1 \end{pmatrix} \begin{pmatrix} X\\ Y\\ Z\\ 1 \end{pmatrix}$
注1：这里的 $x_0$ 、 $y_0$ 其实应该为 $p_x$ 、 $p_y$ ，为了表述方便才这样描述；
注2：这里的 $u,v,x_0,y_0,f_x,f_y$ 都是以像素为单位！

$x_0,y_0,f_x,f_y$ 有四个

R三个

t三个

3.关于R和t的几何意义

根据下式

⎛ ⎝ ⎜ X c a m Y c a m Z c a m ⎞ ⎠ ⎟ = R ⎡ ⎣ ⎢ ⎛ ⎝ ⎜ X Y Z ⎞ ⎠ ⎟ - C ˜ ⎤ ⎦ ⎥ = R ⎛ ⎝ ⎜ X Y Z ⎞ ⎠ ⎟ + t = r 1 X + r 2 Y + r 3 Z + t

$\begin{pmatrix} X_{cam}\\ Y_{cam}\\ Z_{cam} \end{pmatrix}=R\left [ \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} - \widetilde{C}\right ]= R \begin{pmatrix} X\\ Y\\ Z \end{pmatrix} +t= r_1X+r_2Y+r_3Z+t$

旋转矩阵R的三个列 $r_1,r_2,r_3$ 分别表示世界坐标系三轴在摄像机坐标系下的方向
平移向量t表示世界坐标系原点在摄像机坐标系下的坐标；另外， $t = -R \widetilde{C}$ 中， $\widetilde{C}$ 表示摄像机光心在世界坐标系下的坐标
综上，世界坐标系先移动 $-\widetilde{C}$ 到摄像机坐标系光心位置，然后，再经过旋转矩阵R，可以与摄像机坐标系重合！

这里写图片描述

4.刚体变换

欧式空间中一个点P，它在两个坐标系下的坐标分别为 $p = (x,y,z)^T$ 和 $p' = (x',y',z')^T$ ，根据刚体变换的性质，P点在两个坐标系下的坐标具有如下关系：

p' = R p + t

$p' = Rp + t$

即点P在第二个坐标系下的坐标 $p' = (x',y',z')^T$ 可由其在第一个坐标系下的坐标 $p = (x,y,z)^T$ 通过旋转R和平移t而得到

t为第一个坐标系的原点在第二个坐标系下的坐标

$p' = R (0, 0, 0) T + t = t$ $p' = R (0,0,0)^T + t = t$
$R=[r_1,r_2,r_3]$ 的三个列向量分别是第一个坐标系的三个坐标轴在在第二个坐标系下的方向

$p' = R (1, 0, 0) T = r 1$ $p' = R (1,0,0)^T = r_1$
$p' = R (0, 1, 0) T = r 2$ $p' = R (0,1,0)^T = r_2$
$p' = R (0, 0, 1) T = r 3$ $p' = R (0,0,1)^T = r_3$

这里写图片描述

注：到底什么是在某一个坐标系下的坐标？例如， $(a,b,c)^T$ 是点A在某个坐标系 $o-xyz$ 下的坐标，就是说，空间点A的方向矢量OA可以表示为

O A = a * o x + b * o y + c * o z

$OA = a*ox + b*oy + c*oz$
其中，

ox,oy,oz $ox,oy,oz$ 分别为坐标系

o−xyz $o-xyz$ 三个坐标轴的单位矢量

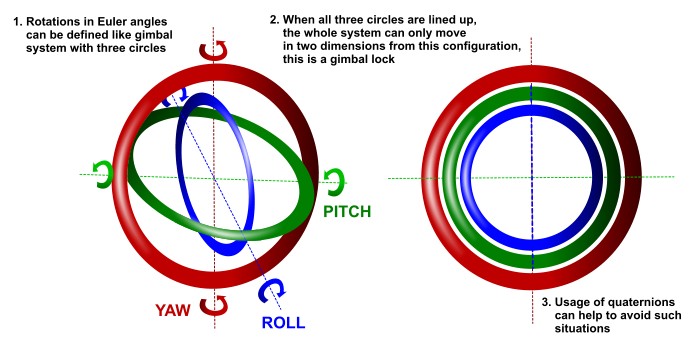
5.欧拉角Euler angles

要实现对刚体的旋转，有许多描述方法；上面的旋转矩阵R是一种描述方式，欧拉角（俯仰角、偏航角、横滚角）也是一种非常直观的表示方法；

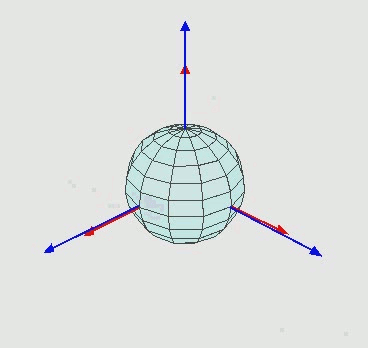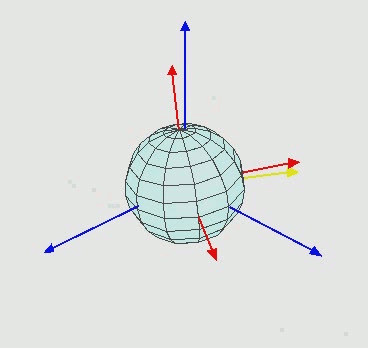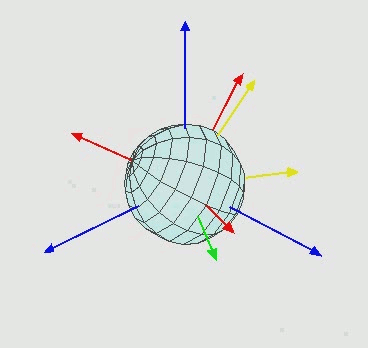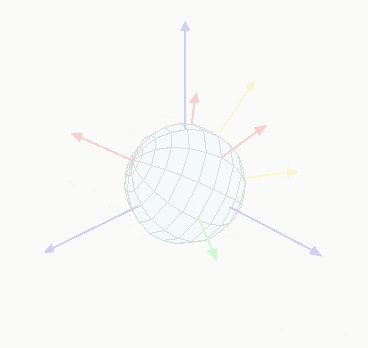
下图的动图显示了一个从欧拉角角度描述的三维旋转（由蓝色坐标轴，转到最终的红色坐标轴，实现了一个3-1-3型一个旋转）：

先绕z轴旋转一个角度
再绕x轴旋转一个角度
最后，又绕z轴旋转了一个角度

欧拉角的表述形式是可以转换为旋转矩阵的形式的！

这里写图片描述

下图展示了3-1-2的欧拉角旋转
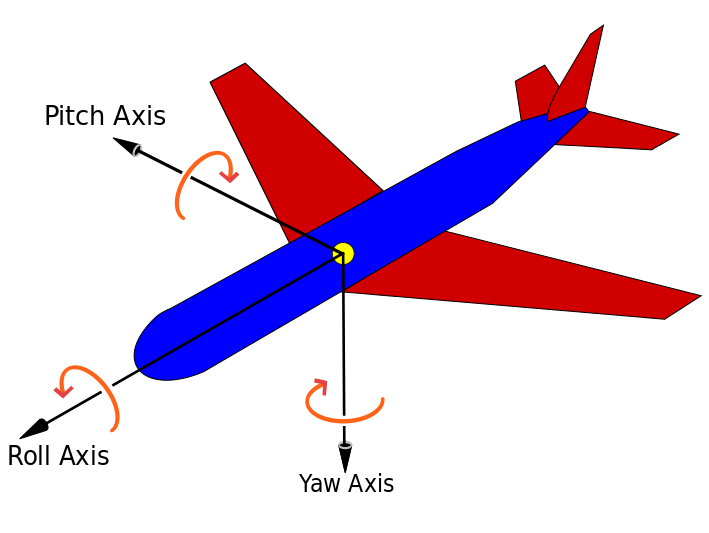
这里写图片描述

下图是以飞行器为例的一个欧拉角的表示形式：

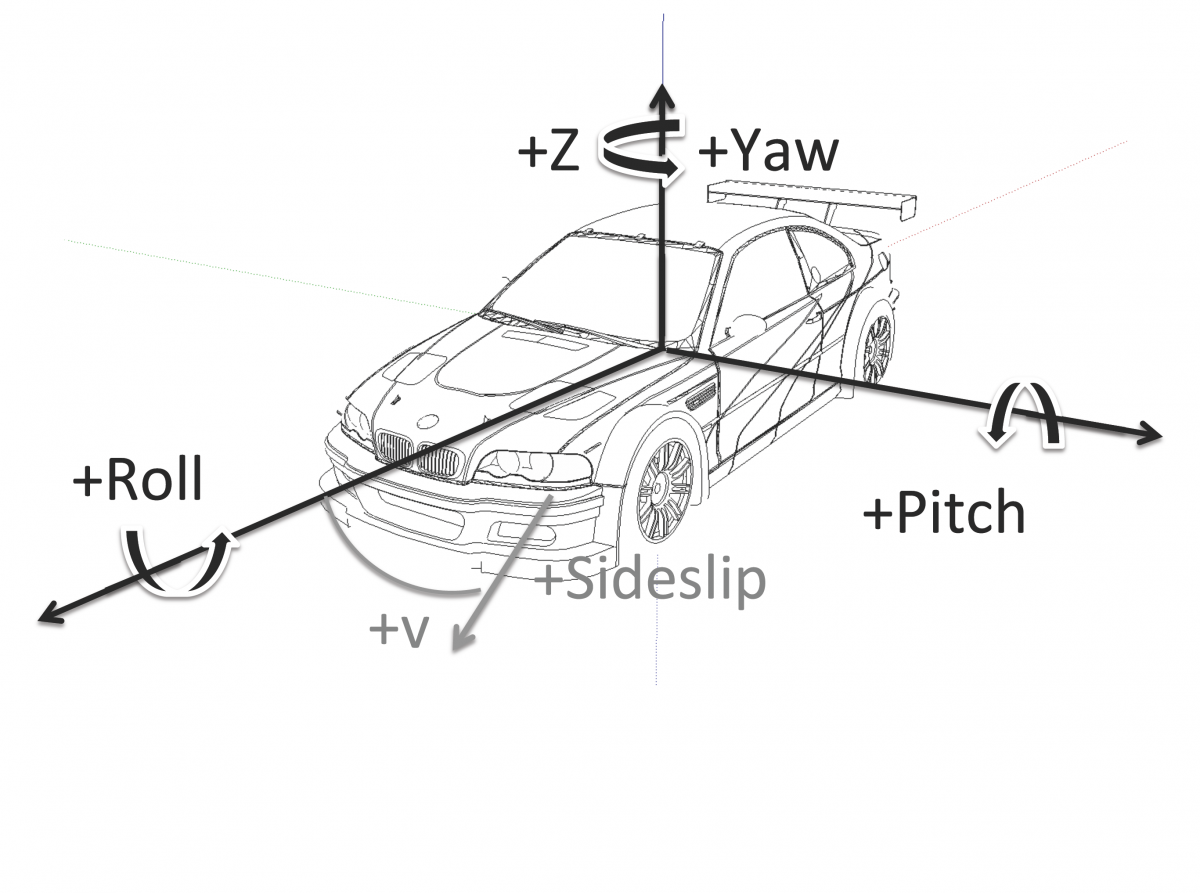
这里写图片描述

下图是以汽车为例的一个欧拉角的表示形式：
这里写图片描述

6.四元数unit quaternions

除了欧拉角和旋转矩阵外，还有一种称为欧拉轴角的描述方式：绕某一个轴旋转某一个角度（轴+角，它描述了绕任意轴的一个旋转）；由欧拉轴角可以构造出一个四维向量–四元数：

四元数是一个四维向量 $(q_0,q_1,q_2,q_3)$
$(x,y,z)$ 表示的旋转轴的方向信息
$q_0$ 表示的是绕旋转轴的旋转角信息

这里写图片描述
注：该图来自http://blog.db-in.com/cameras-on-opengl-es-2-x/#quaternions

具体地，四元数与欧拉轴角之间的关系如下：

这里写图片描述

Reference
[1] Multiple View Geometry in Computer Vision (Second Edition). Andrew Zisserman.Chapter 6 Camera Models.
[2] 机器视觉. 张广军
[3] 维基百科·四元数和欧拉角转换 https://en.wikipedia.org/wiki/Conversion_between_quaternions_and_Euler_angles
[4] Understanding Quaternions. http://www.chrobotics.com/library/understanding-quaternions