针孔相机模型
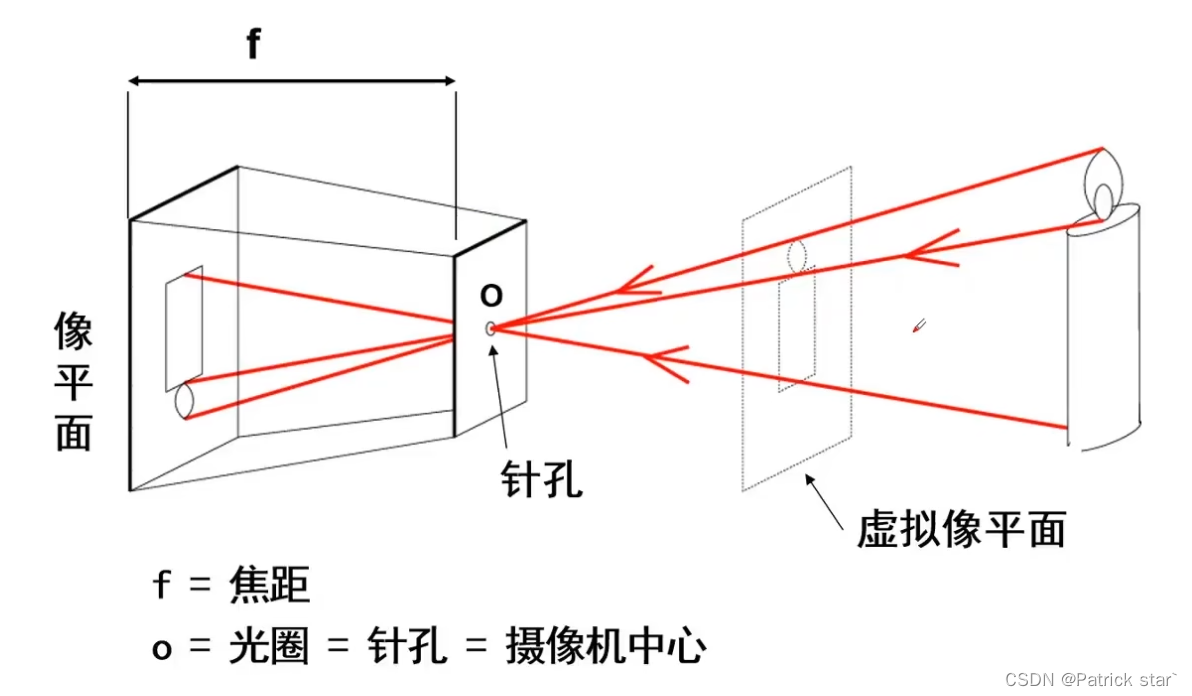
为了方便我们对针孔相机模型进行数学建模,我们往往对虚拟像平面进行研究,因为虚拟像平面的方向与我们实际物体的方向一致。

通过相似三角形法可以得到三维坐标到二维坐标映射
将像平面原点坐标移动到左下角:
加上现实世界单位(m)到数码图片单位(pixel)的转换量:

至此,完成了相机坐标到像平面坐标的映射:
齐次坐标
在上面这个公式中,z是会改变的,因此 P到P'并不是线性变换,我们需要引用齐次坐标,使它成为线性变换。
欧式坐标变为齐次坐标就是在最后增加一个维度,并让它的值为1。
齐次坐标转为欧式坐标:
齐次坐标转到欧式坐标的结果并不是一一对应的,比如(1,1,1)和(2,2,2)转到欧式坐标都是(1,1),它们之间相差一个系数。
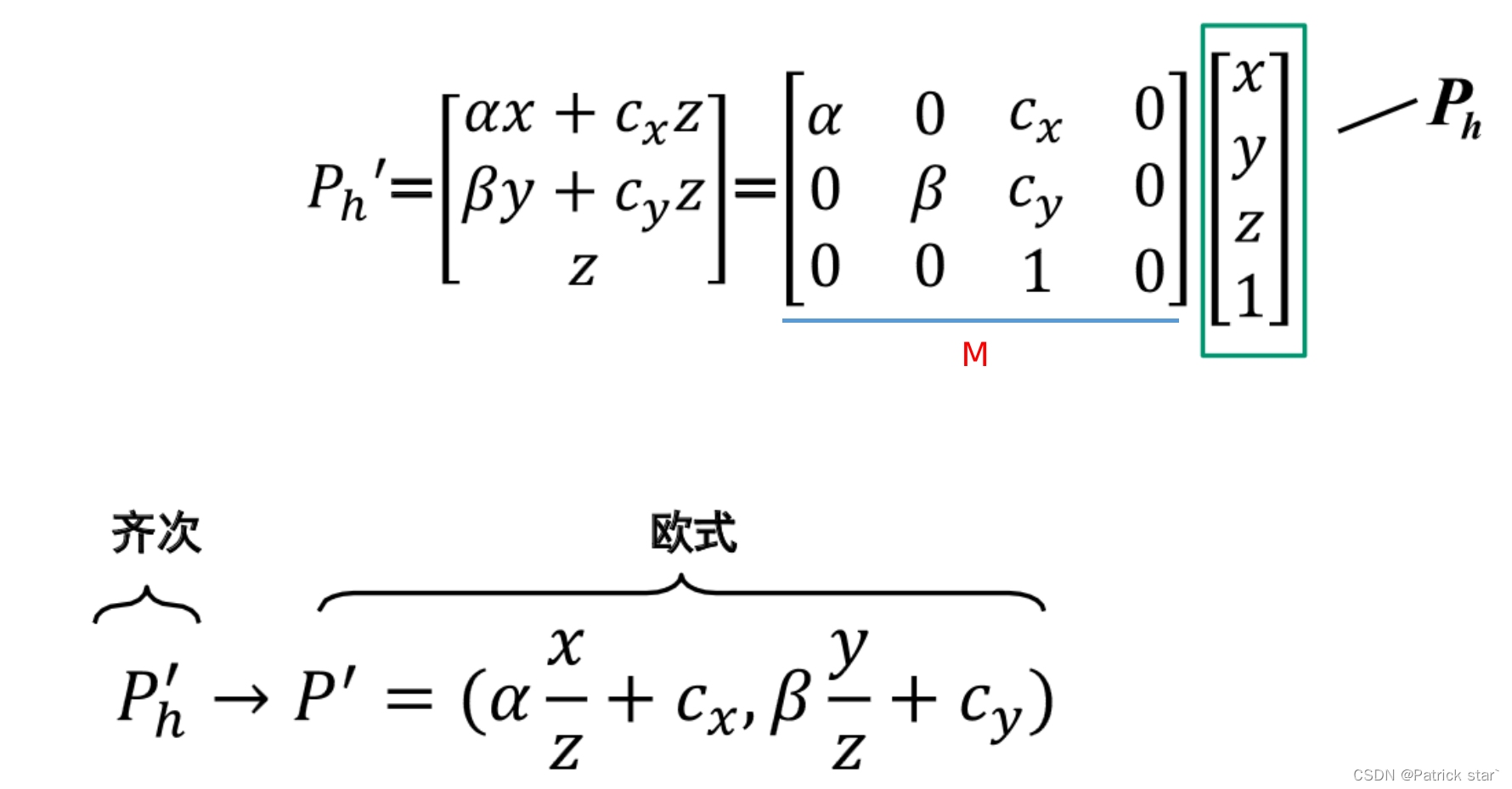
M矩阵中的元素是固定不变的,变为齐次坐标后P到P'就是线性变换了。
投影矩阵
由于制造工艺的原因,像平面可能不是一个矩形,所以需要映入进行建模。
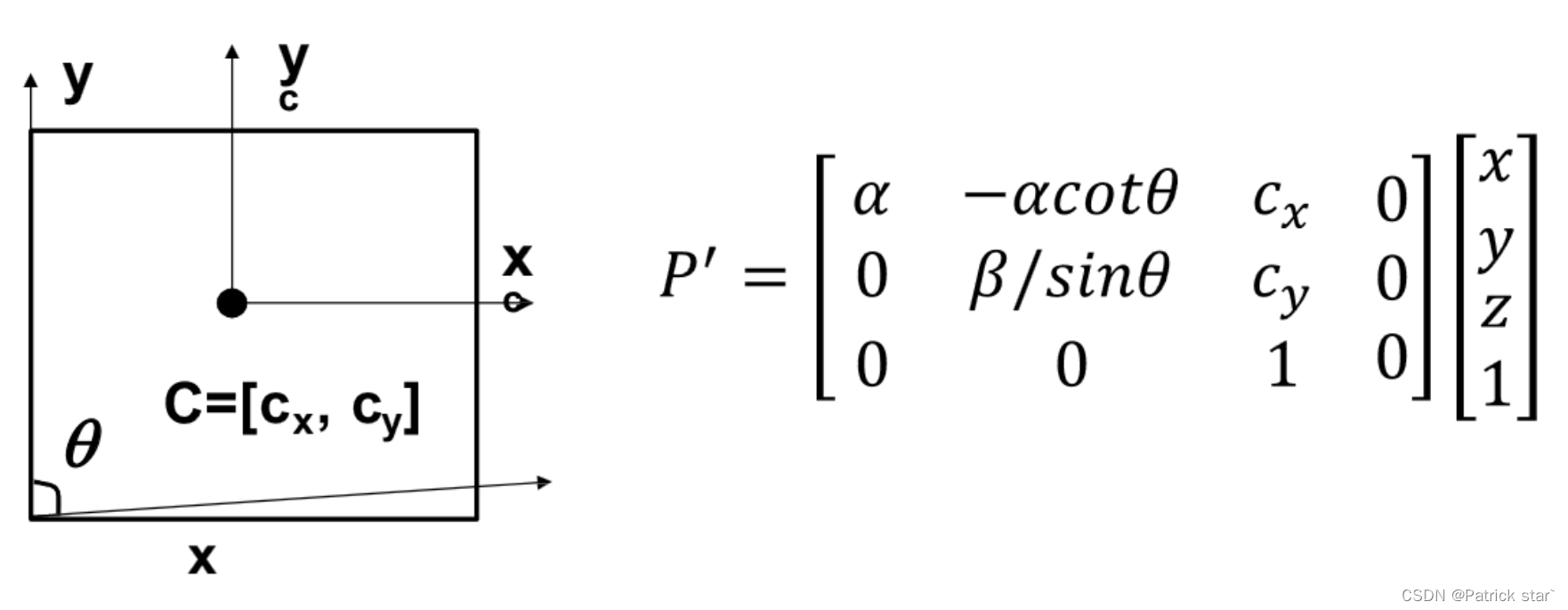
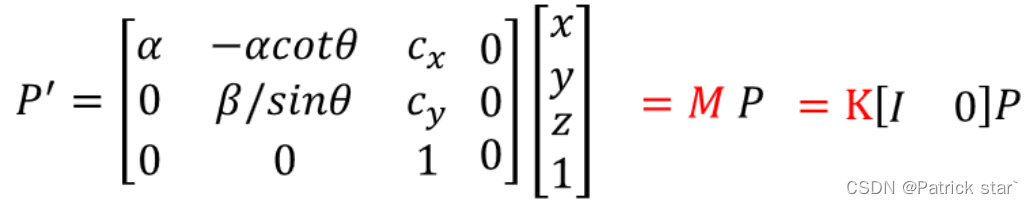
我M称为投影矩阵, K称为摄像机的内参矩阵。
我们目前所完成的是相机坐标系到像素坐标系的映射,还需要一个外参矩阵,建立世界坐标系到相机坐标系的映射。
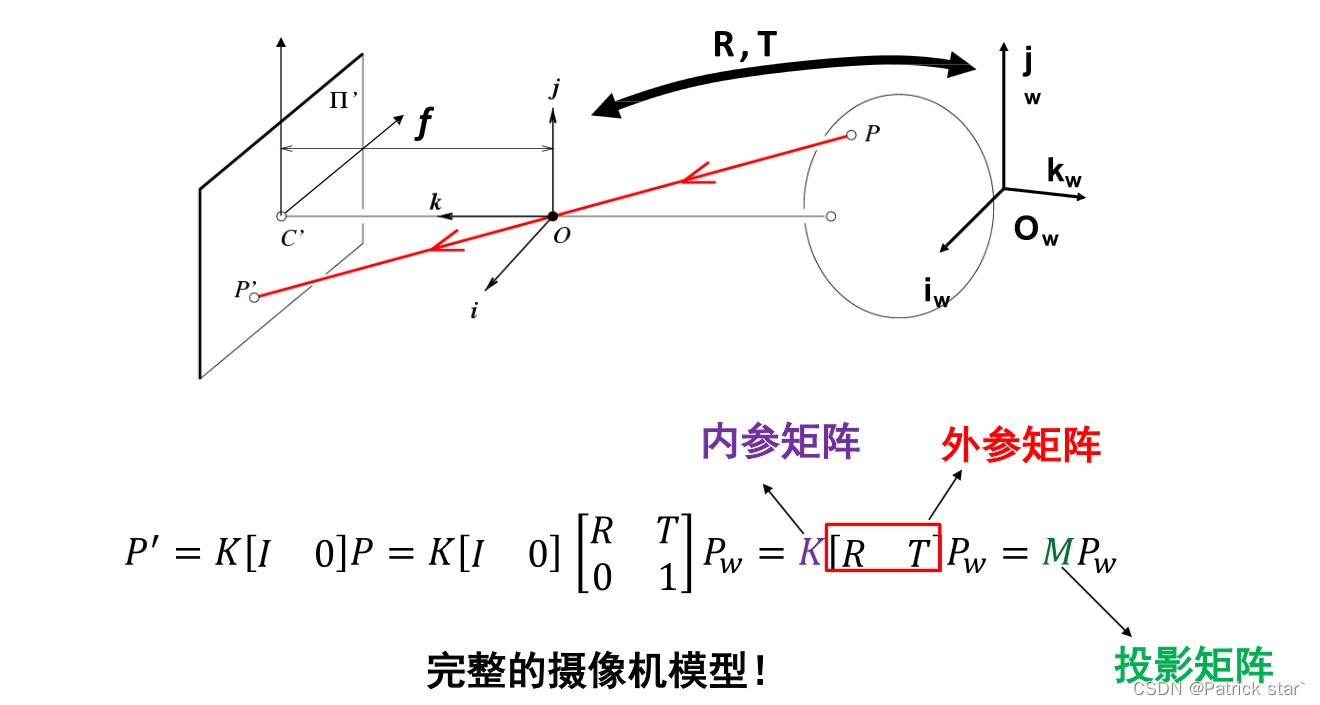
参考鲁鹏老师三维重建课: