排序算法的速度
取决于所使用的计算机模型里允许的操作。
常见排序
快速排序(Θ(nlgn))(不稳定排序)(交换过程会破坏稳定性)
堆排序 (Θ(nlgn))(不稳定排序)
归并排序(Θ(nlgn))(稳定性排序)
插入排序(Θ(n^2)) (稳定性排序)
比较排序模型
允许比较数的大小的操作。
最快的时间复杂度为Θ(nlgn)。
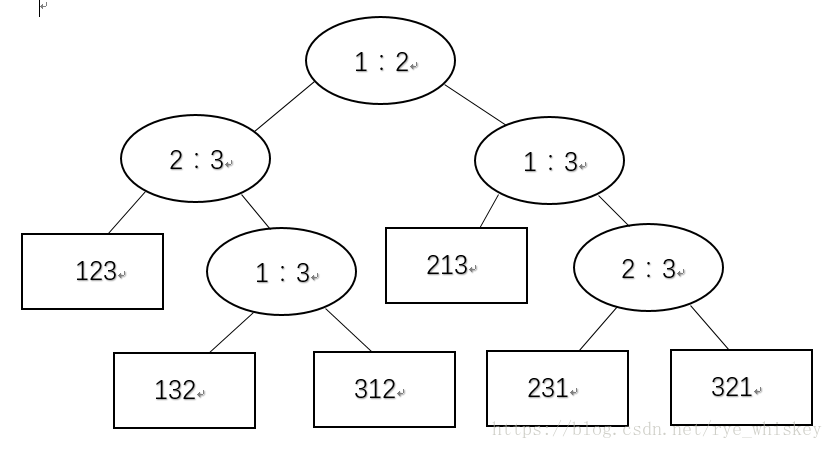
决策树模型
Ex:对<a1,a2,a3>排序
一般情况下,对<a1,a2,a3,…,an>排序:
每一个内节点为i:j (i,j∈{1,2,…,n})。
比较ai和aj的大小。
如果ai<=aj 则走左子树,反之,则走右子树。
每一个叶节点代表一个排序。
将比较排序转化为决策树排序:
- 步骤:
为每一个n值绘制一个决策树。
进行比较时把树分为两个分支,左子树和右子树。
决策树会把所有比较结果得到的排序都列出来。
决策树指出了算法执行过程中所有可能的路线。
决策树只针对确定性的算法,不适用于随机化的算法。 - 运行时间:
运行时间取决于比较的次数,所有比较的次数会决定决策的高度。
最坏情况的路线会为决策树最大高度。 - 证明决策树的最小高度要大于nlogn:
决策树的叶节点数>=n!
对于高度为h的决策树 叶节点数<=2^h
则有n!<=2^h
h>=lg(n!)
h>=lg((n/e)^n)(斯特林(stirling)公式)
h=nlg(n/e)
h=n(lgn-lge)
h=Ω(nlgn)
- 步骤:
在基于比较的排序算法中,归并排序和堆排序是渐进最优的,随机化快速排序对于每一个n会有不同的决策树,它们按概率出现,但所有决策树都符合上述证明过程,所以也是渐进最优的。
排序的稳定性
一个稳定性算法保证了相等元素的相对顺序
线性时间排序
计数排序:
计数排序适用于小范围数据的排序,是稳定性排序算法。
1.输入为一个数列A[1,…,n] A[i]为整数且在1~k的范围内。
2.输出为数列A的排序数列B[1,…,n]。
3.辅助存储数列C[1,…,k]。
伪码:
for i ← 1 to k //值初始化C数组。
do C[i] ← 0
for j ← 1 to n 。//在C数组中统计对应下标值在A中出现的次数。
do C[A[j]] ← C[A[j]]+1
for i ← 2 to k //C数组中计算小于等于下标值在A中出现次数。
do C[i] ← C[i]+C[i-1]
for j ← n downto 1 //根据C数组在B数组中排序(保持稳定)。
do B[C[A[j]]] ← A[j]
C[A[j]] ← C[A[j]]-1
Ex:
A=4 1 3 4 3 C=0 0 0 0
C=1 0 2 2
C‘=1 1 3 5
B=0 0 3 0 0 C‘=1 1 2 5
B=0 0 3 0 4 C‘=1 1 2 4
B=0 3 3 0 4 C‘=1 1 1 4
B=1 3 3 0 4 C‘=0 1 1 4
B=1 3 3 4 4 C‘=0 1 1 3
运行时间为O(n+k),当k<=n时,这个算法效率比较高。
基数排序:
基数排序适用于大范围数据的排序(古老的排序算法)。
从最后一位开始,依次按位排序(必须采用稳定性的排序)。
Ex:
329 720 720 329
457 355 329 355
657 436 436 436
839 457 839 457
436 657 355 657
720 329 457 720
355 839 657 839
算法正确性证明(归纳法):
基本情况是,只有一位数字的数组,对它进行排序即可完成数组排序。
对第t位的排序,应有前t-1位都已经进行了排序的前提假设,在对第t位进行排序时会有两
种情况,当两个数字的第t位相同时,对第t位的稳定排序即可保证它们的相对位置不变,排
序会按照t-1位的数字进行排序,符合排序要求,当两个数字的第t位不相同时,对第t位的
进行排序后的结果同样符合排序要求,所以该算法可以实现数组的排序。
算法一般性描述分析:
1.每一轮用计数排序。
2.假设数字用b位数表示 数的范围为0~2^b-1。
3.将b位数拆分为b/r位数字 b/r即为要处理的轮数。
4.运行时间为O(b/r·(n+k))=O(b/r·(n+2^r)) 。
5.对b/r·(n+2^r)中的r求导,求导数为0时的解,以获得最小值。
6.可知2^r<=n,r尽量取大值时 r=lgn。
7.此时运行时间为O(bn/lgn) 如果数字范围为0~2^b-1或是说0~n^d-1。
那么运行时间为O(dn) 如果d=O(1)那么运行时间为O(n)。
因为计数排序在辅助空间的分配使用方面会有时间消耗,所以在实践中基数排序速度并不是很快。
对于一字长的数组成的数组,并且可以在线性时间内操作一个字,目前已知的最好排序算法的期望运
行时间为O(n*(lg(lgn))^(1/2))。