顺序统计问题:
有n个无序的数,找到第k小的数(所有元素的值不相等)。
朴素算法:
先排序,第k号元素即为第k小的数。
k=1时,即为最小值。
k=n时,即为最大值。
k=(n+1)/2向上或向下取整时,即为中位数。
随机选择算法(随机化的分治算法):
定义函数Rand-Select(A,p,q,i)。
在数组A中获得第i小的数。
- 用分治策略可在数组的一部分A[p…q]中找第i小的数。
1.如果p=q则返回A[p]。
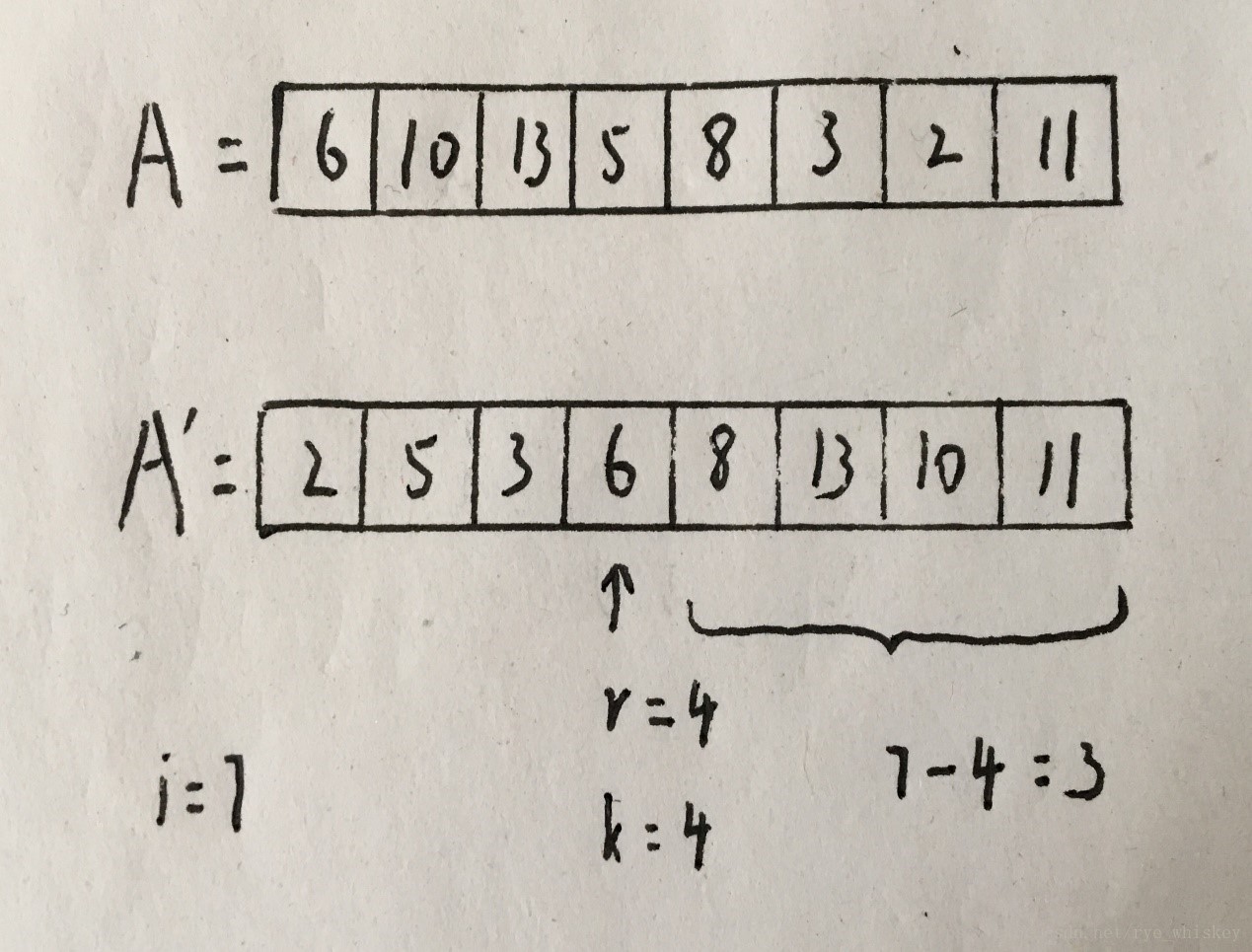
2.r ← Rand-Partition(A,p,q)。
3.k ← r-p+1,k是划分元素的序号。
r的左边和右边分别是小于和大于r元素的数。
4.如果i 等于 k即为所求值。
如果i 小于 k那么返回Rand-Select(A,p,r-1,i)。
如果i 大于 k那么返回Rand-Select(A,r+1,q,i-k)。 - Ex:
- 运行时间:
- 好的情况:
划分时,按1/10 9/10划分。
T(n)<=T(9/10·n)+Θ(n)= Θ(n) - 坏的情况:
划分时,按0 n-1划分。
T(n)=T(n-1)+Θ(n)=Θ(n^2) - 运行时间的期望:
- 好的情况:
最坏情况为线性时间复杂度的算法:
保证一个好的主元。
数组大小为n获得第i小的元素。
- 算法步骤
1.将数组画成5*(n/5)的方阵,找到每一组(五个数)的中值(时间复杂度为Θ(n))。
2.递归的计算每一组中值的中值x(T(n/5))。
3.把x作为划分主元,进行划分 k ← x-p+1(T(n))。
4.如果i 等于 k即为所求值。
如果i 小于 k那么递归的继续处理数组的小值部分。
如果i 大于 k那么递归的继续处理数组的大值部分(T(c·n) c应该要小于4/5)。 运行时间:
在5*(n/5)的方阵中可以分析出有至少3·[[n/5]/2]向下取整数量的数小于x。 即有至少3·[n/10]向下取整数量的数小于x。 当n足够大,时n/10取整再乘以3一定比n/4大。 可得T(n)<=T(n/5)+T(3/4n)+Θ(n)。 代换法证明线性时间复杂度: 假设T(n)<=c·n。 则有T(n)<=1/5·cn+3/4·cn+Θ(n) =19/20·cn+Θ(n) =cn-(1/20·cn-Θ(n)) 当c足够大时 (1/20·cn-Θ(n))非负。 即证得此算法的最坏时间复杂度为线性时间复杂度。