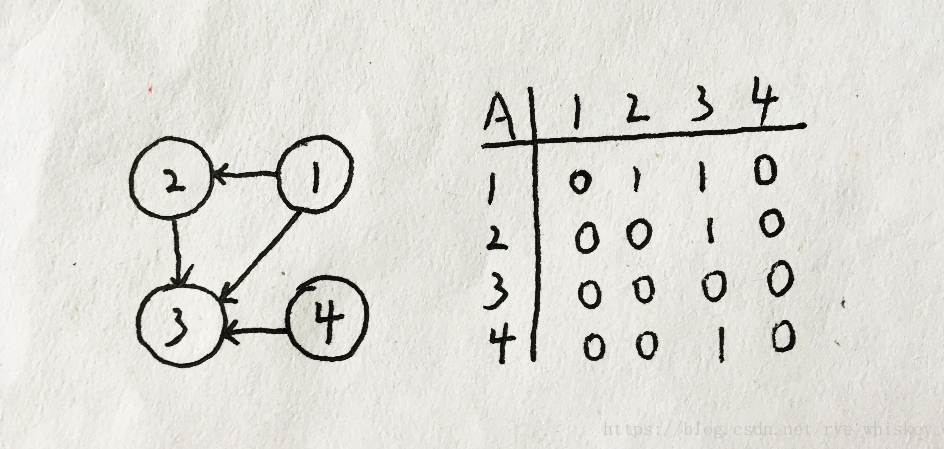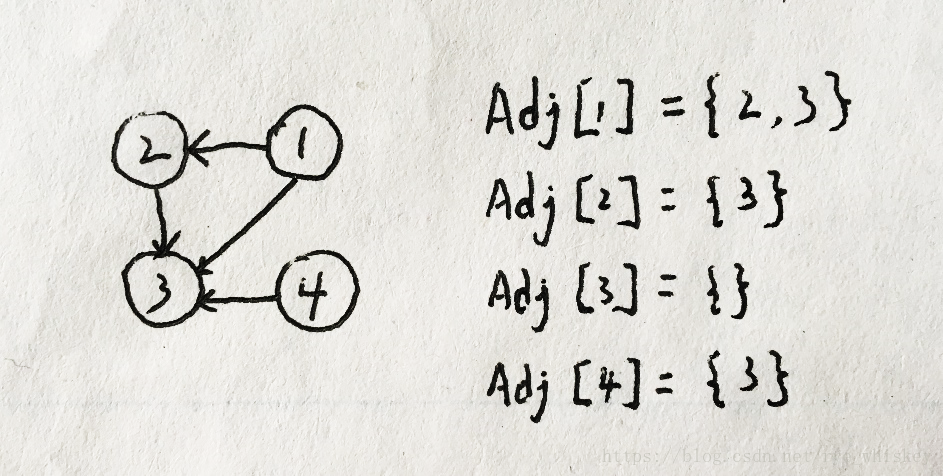关于图的知识回顾(附录B)
有向图(Digraph,Direct graph)G=(V,E),V为图的顶点集,E为边集,E∈V x V。
无向图(Undirected graph)G=(V,E),E为无向的边集。
|E|=O(V^2)
连通图,对于图中的任意顶点,总有路径可以到达其他顶点,|E|>=|V|-1。
对于连通图,则有lg|E|= O(lg(V^2))=O(lgV)=Ω(lg(|V|-1))=Ω(lgV)=Θ(lgV)。
图的表示
- 邻接矩阵:
图G=(V,E),设V为{1,2,…,n},邻接矩阵则是一个n x n的矩阵A,且当(i,j)∈E时,A[i,j]=1,否则A[i,j]=0。
- Ex:
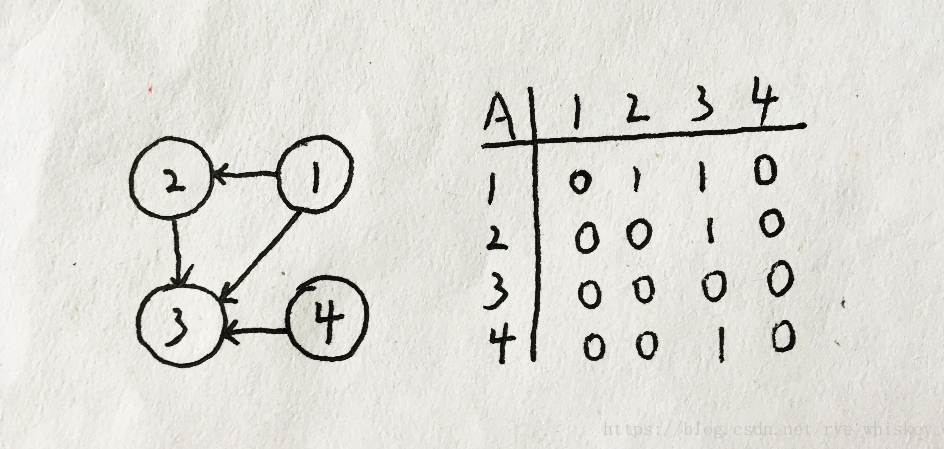
存储空间占用情况为Θ(V^2),用于稠密图(边数尽可能的多)的存储效果会比较好。
邻接矩阵可用一位表示每一条边的情况。
稀疏图例子:链表、平面图,自由树。稠密图例子:完全图。
- 邻接表:
链表Adj[v]为所有与v邻接的点的集合。
Ex:
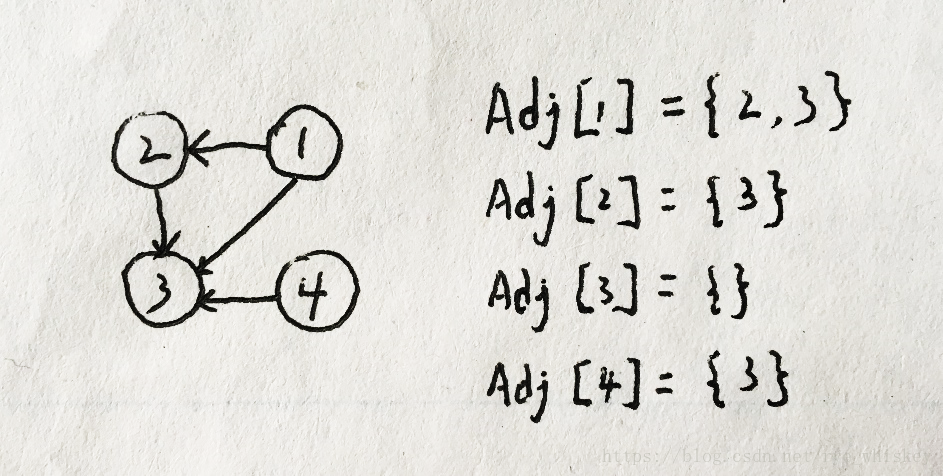
可见链表的长度|Adj[v]|,也就是无向图中顶点v的度,有向图中顶点v的出度
- 握手定理:设G=(V,E)为任意无向图,则所有顶点的度数和=2·|E|。
邻接表的存储空间占用情况为Θ(V+E),用于稀疏图的表示。
- 邻接表需要使用O(lgV)位来表示一个顶点(数量为V,可用O(lgV)位编码每一种)。
- 矩阵和图是看待同一种事物的两种不同方式,相似的性质可能同时出现在这两者中。
注:附录B中关于树给出一些定义和性质,很值得看一看。
最小生成树
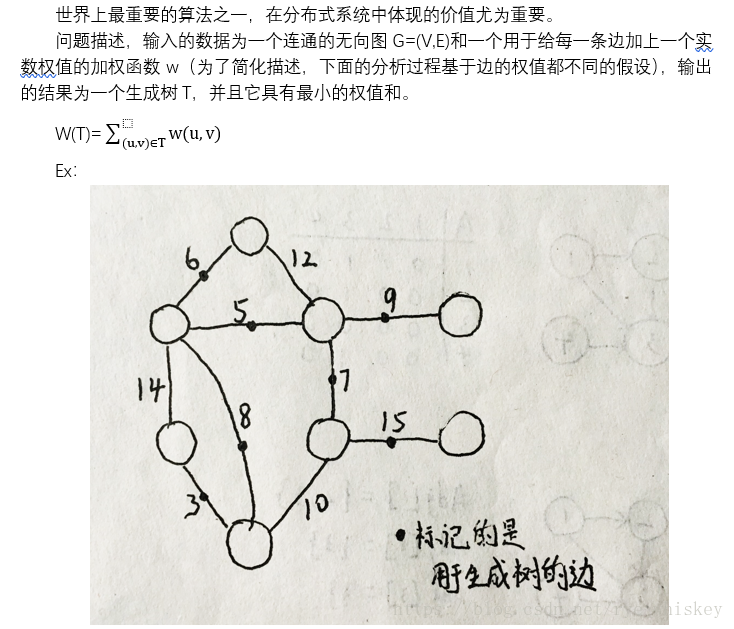
MST动态规划思路
- 最优子结构分析:
最小生成树MST T(图的其他边都被忽略):
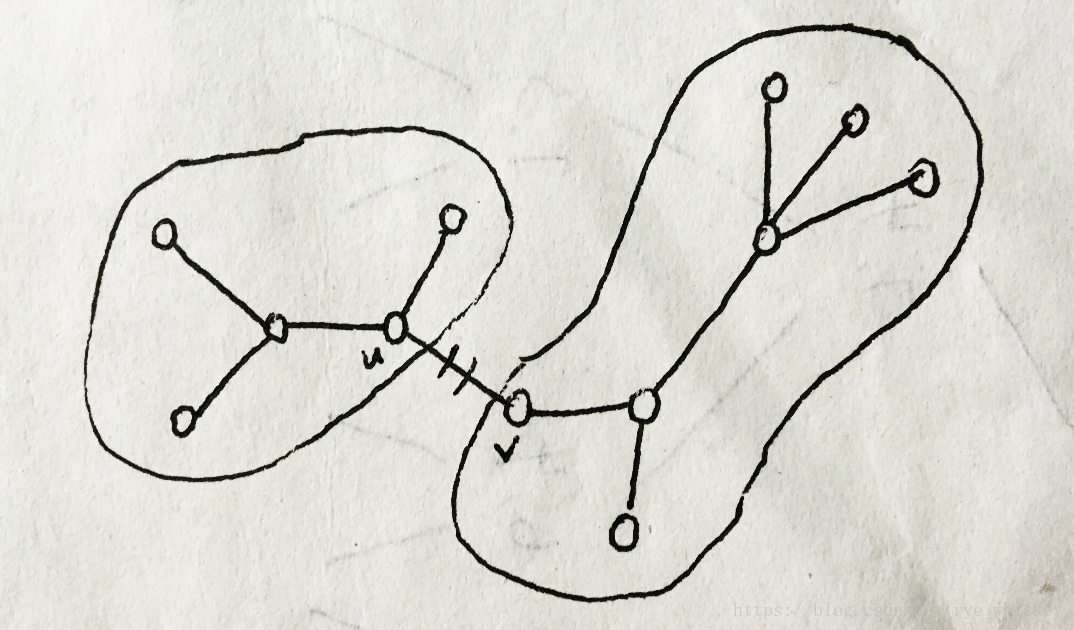
删除(u,v)∈T,那么最小生成树T被分为两个子树T1和T2。
- 证明定理:
设图G1=(V1,E1)为原图G的一个子图,且满足V1为T1中的所有顶点,而边集E1={(x,y)∈E,x,y∈V1},那么T1为G1的最小生成树(同理T2也有这样的结果)。
- 剪贴法(Cut & Paste):
W(T)=w(u,v)+W(T1)+W(T2)
假设图G1有个比T1权值和更小的生成树T1‘,那么显然,就会有W(T)=w(u,v)+W(T1’)+W(T2),与W(T)=w(u,v)+W(T1)+W(T2)相矛盾,所以假设不成立,上述定理得证。
- 重叠子问题分析:
在删除(u,v)划分子树的过程中,不同的删除顺序中划分出相同的子树。
最小生成树问题具有重叠子问题。
- 综上可知,最小生成树可以使用动态规划。
贪婪算法(Greedy algorithm)问题特性
问题中存在一个局部最优解同时也是全局最优解。
MST贪婪算法思路
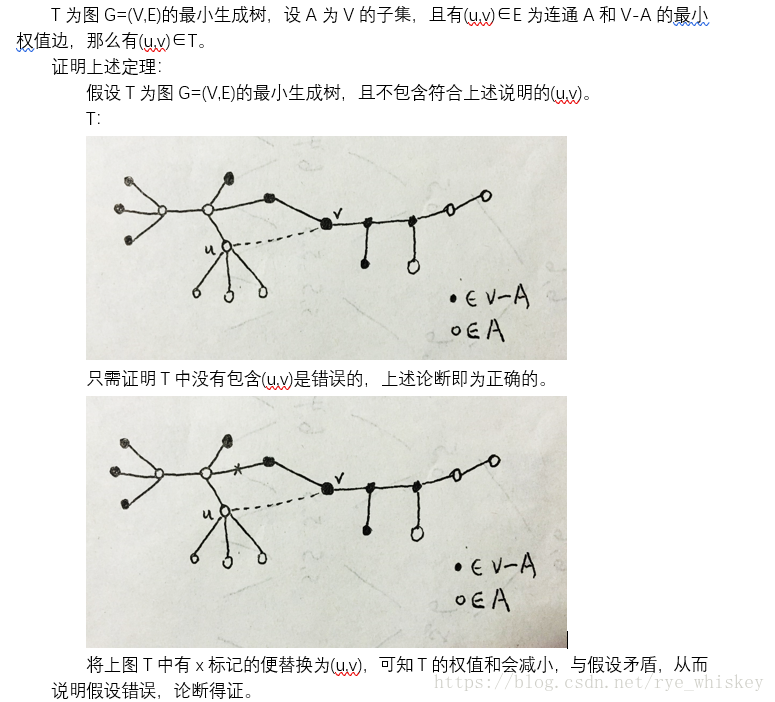
Prim算法