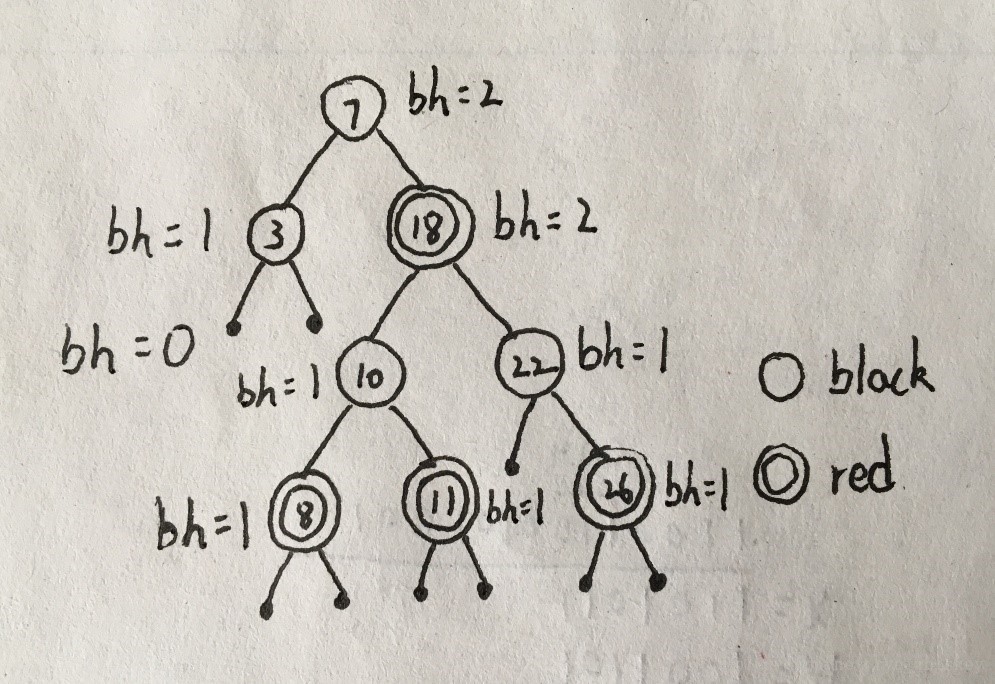平衡搜索树
一种搜索树结构,其维护一个n个元素的动态集,树高为O(lgn)。
不同的平衡搜索树数据结构
AVL trees
2-3 trees
2-3-4 trees
B trees
Red-black trees
Skip lists
Treaps
红黑树
红黑树是二叉搜索树,其每个结点都会附带一些额外的信息,被称为色域,
红黑树的特性
1.每个结点的色域值为黑色或红色,因此只需一个位来标明结点的色域。
2.树的根结点和叶节点的色域值为黑色。(叶结点为外部结点,其他为内部结点)
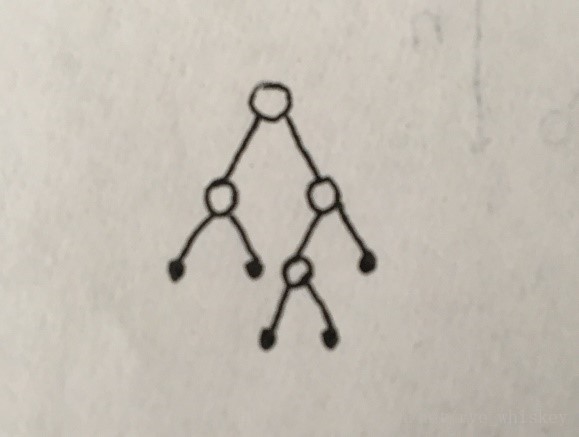
3.每个红色结点的父结点都是黑色。
4.从树中任意一个结点x一直到x的子孙叶结点的路径中的黑色结点数(black-Height(x))都相等,black-Height(x)不将x结点计算在其中。
红黑树的高度
- 证明由n个值创建的红黑树的高度h<=2lg(n+1):
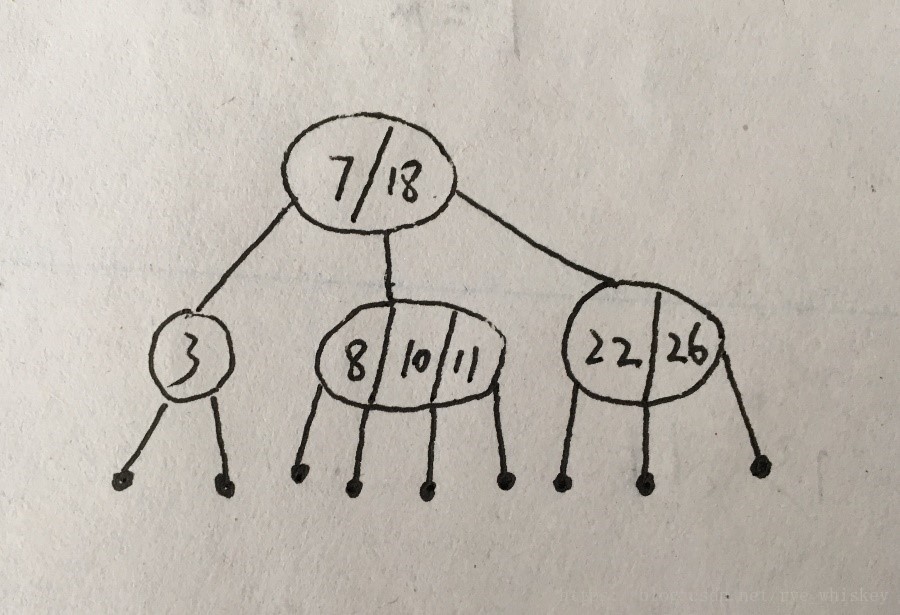
改变红黑树将每个红结点和它的父结点(黑结点)合并起来。
所有内部结点都有2~4个孩子(2-3-4树)。
所有叶结点的深度等于根节点的black-Height,所以它们都相等,在同一层。
叶结点数为n+1,设2-3-4树的高度为h’。
则有2^h’<= n+1<=4^h’
2^h’<= n+1 => h’<=lg(n+1)
由红黑树的特性3可知,原红黑树最长路径中红结点的数目最多占一半。
=> h<=2lg(n+1)
红黑树的查询
进行查询操作,例如查询最大值、最小值、前一个、后一个,都能在O(lgn)时间内完成。
红黑树的更新(插入和删除)
1.使用二叉搜索树的插入和删除操作。
2.改变色域值。
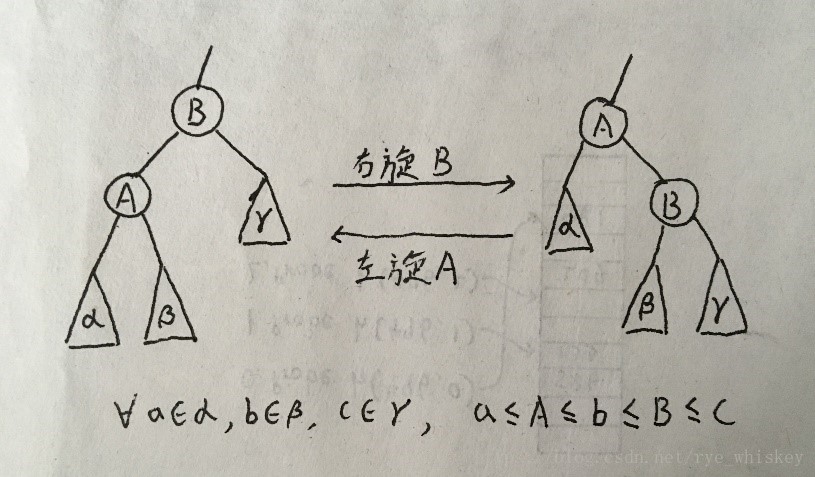
3.通过旋转对树进行重排列。
- 旋转:
旋转为常数时间内的操作。 红黑树的插入:
1.使用BST的插入操作。
2.将插入节点的色域设为红色(保护特性4不被破坏,特性3会被破坏)。
3.把特性3的破坏上移,重新上色,直到可以通过旋转操作完成红黑树的重构,然后可能需要再进行几个重新上色操作。- Ex:
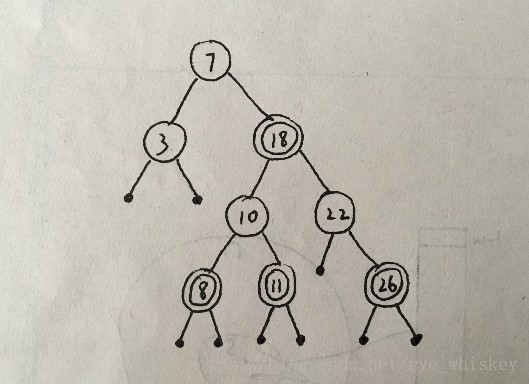
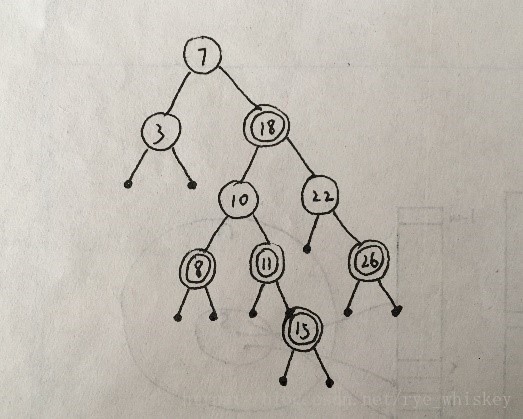
- 在此红黑树中插入15这个结点:
使用BST的插入操作,色域设为红色:
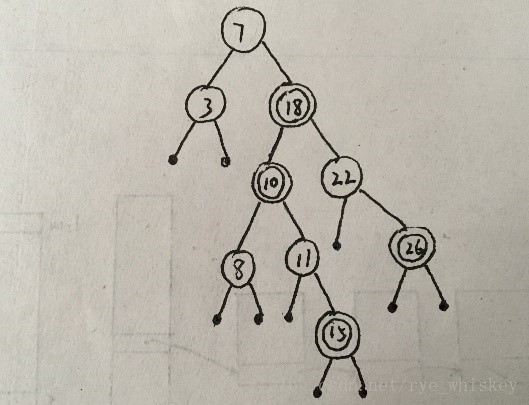
把特性3的破坏上移,重新上色:
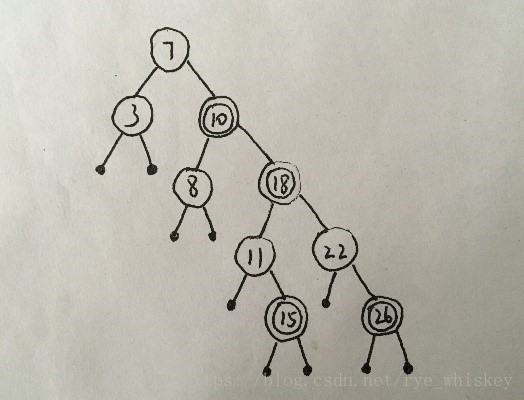
右旋:
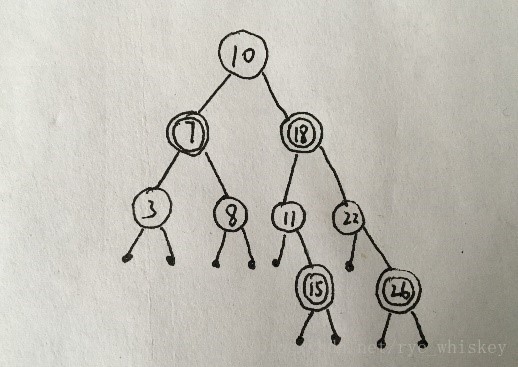
左旋并改色:
这样就完成了红黑树的插入操作。
- 在此红黑树中插入15这个结点:
- Ex:
红黑树的插入操作伪码:
RB-Insert(T,x):
BST-Insert(T,x)
color[x] ← Red
while x≠root[T] and color[x]=red
if p[x]=left[p[p[x]]] //结点x的父结点是父父结点的左孩子(A类情况)。
y ← right[p[p[x]]]
if color[y]=red
<case1>
else if x=right[p[x]]
<case2>
<case3>
else
<case3>
else //结点x的父结点是父父结点的右孩子(B类情况)。
……//对称的处理另外3种情况。
color[root[T]] ← black<case1>改色:
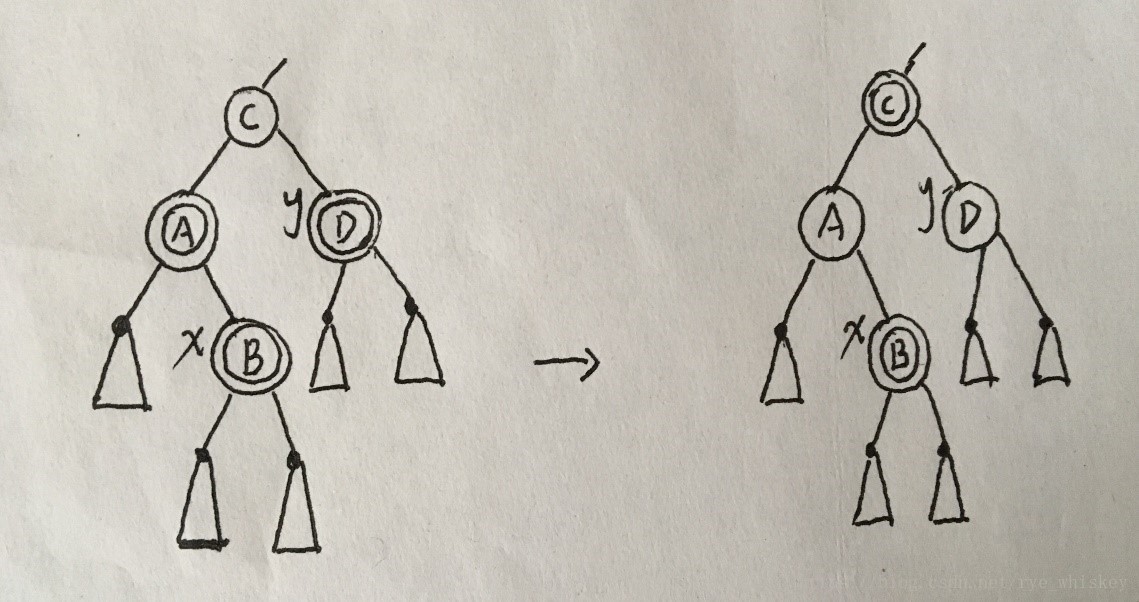
然后将C结点设为x,继续循环。
<case2>左旋:
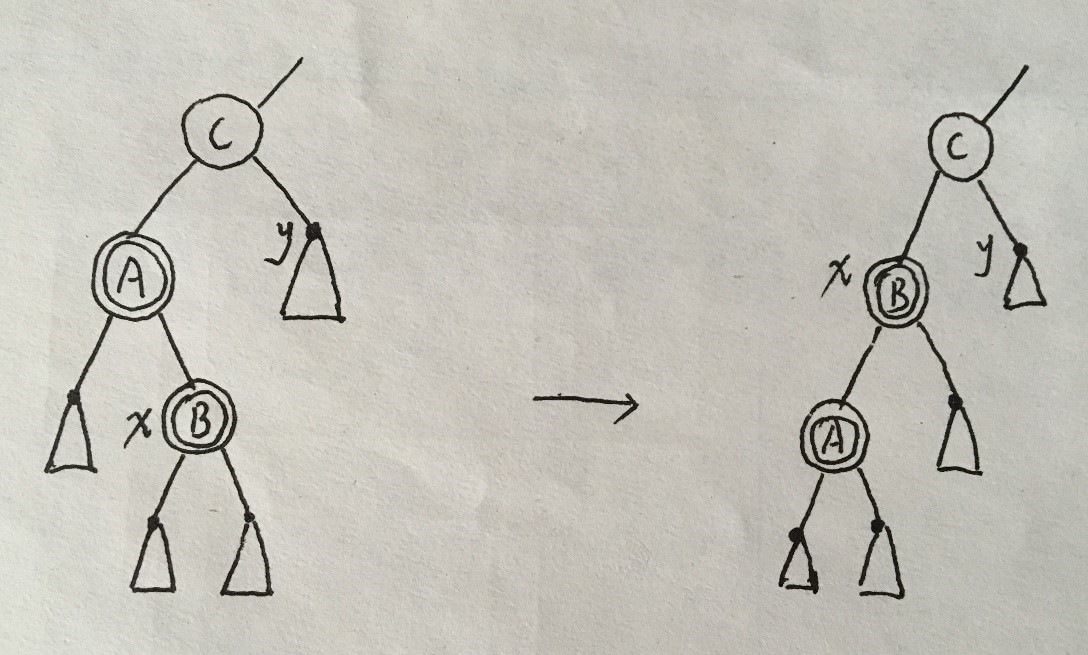
然后将A结点设为x,继续执行的处理操作。
<case3>右旋并改色:

这样就完成了红黑树的重建,可终止循环。
- 红黑树插入操作的时间:
BST的插入操作耗时为O(lgn),二叉树的重建过程中<case2>和<case3>以及改色旋转过程都是
常数时间范围内的操作,<case1>将特性3的破坏上移,明显耗时应该为O(lgn)。
综上,可知红黑树插入操作的时间O(lgn)。