本篇博客将按照机器学习简介中机器学习建模步骤，结合宝可梦（神奇宝贝）具体数据进行案例分析。

Objective

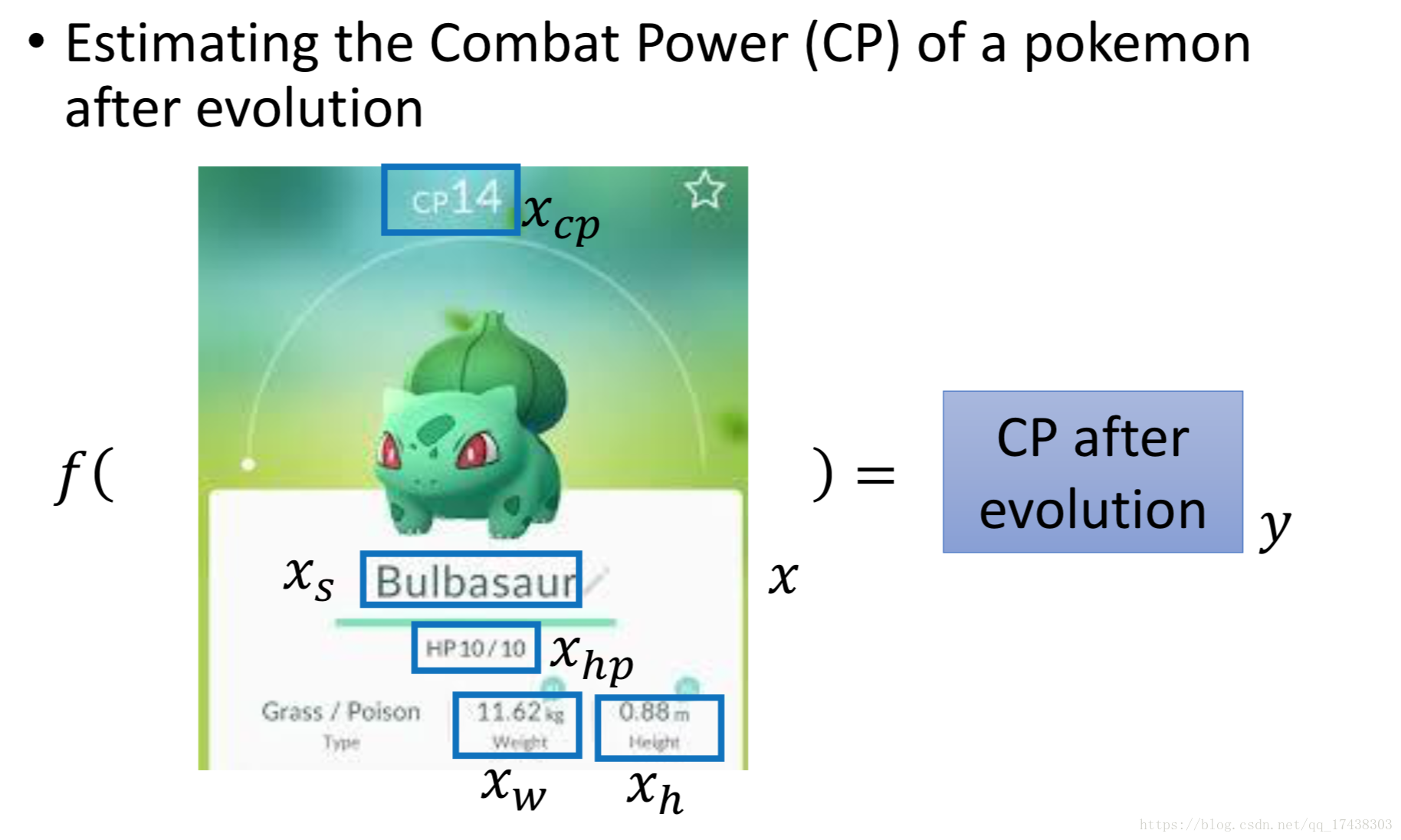
通过训练宝可梦属性的历史数据构建回归模型，输入宝可梦进化前的属性数据，预测宝可梦进化后的Combat Power (CP)。

step1：Model

假设进化前的 $x_{cp}$ 与进化后的的 $x_{cp}$ （即 $y$ ）存在关系 $f_1,f_2\dots f_n,(f_i=b_i+w_ix_{cp},i=1,2\dots n)$

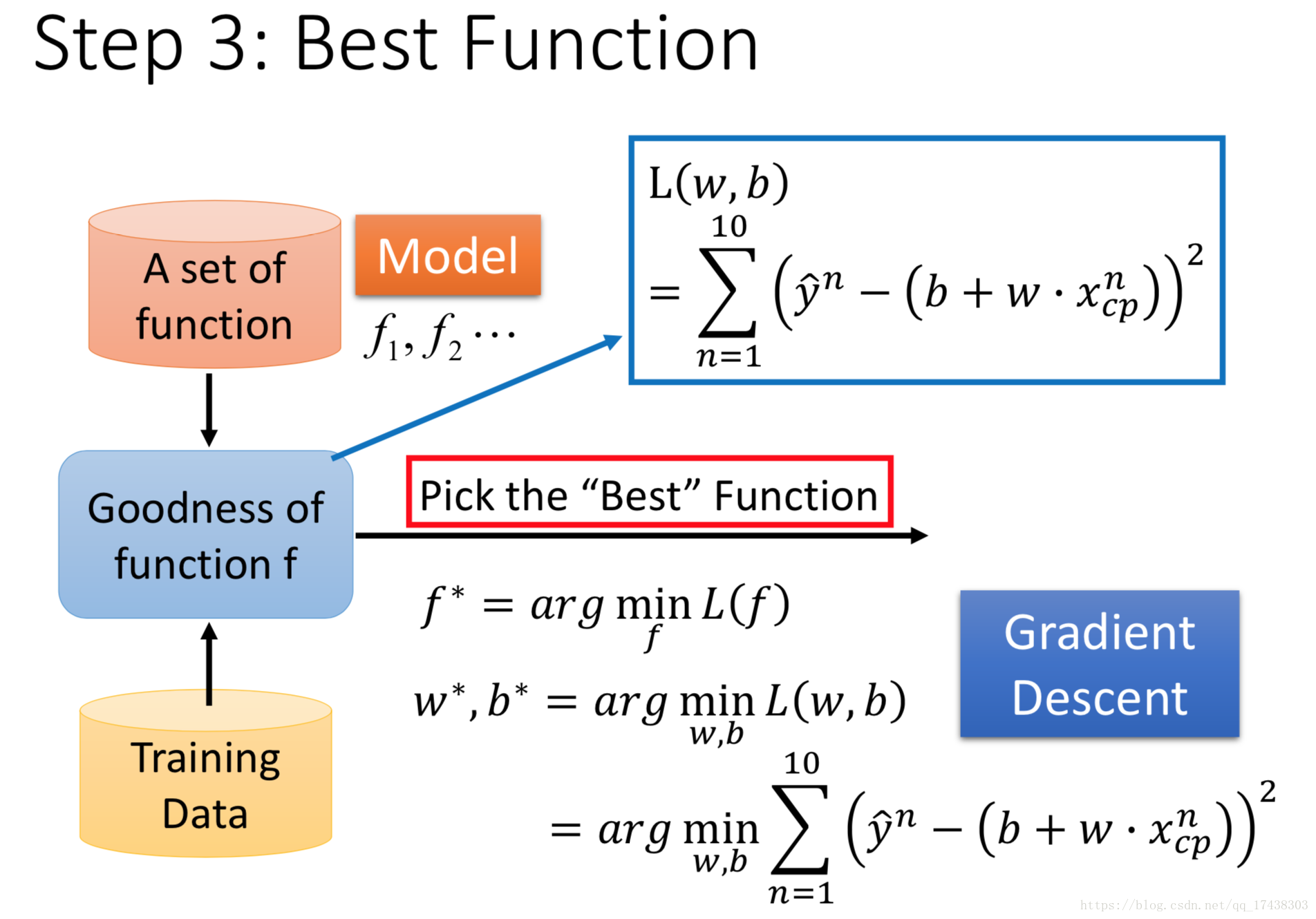
step2：Goodness of Function

$x^i_{cp}$ 表示第 $i$ 个观测（进化前的CP）， $\hat{y}^i$ 表示第 $i$ 个观测的真实值（进化后的CP），现在捕捉10只宝可梦，记录这10只宝可梦进化前和进化后的CP（ $x_{cp}^i,\hat{y}^i,i=1,2\dots10$ ），在这一案例中 $L(w,b)=\sum_{n=1}^{10}(\hat{y}^n-(b+wx_{cp}^n))^2$

Loss function L由 $w,b$ 控制，可视化如图，冷色调代表低L值，暖色调代表高L值，

step3：Best Function

从Step1中的 $f_1,f_2\dots f_n$ 中选择最优函数 $f^*$ ， $f^*=argmin_{f \in F}L(f)$ ，在这一案例中，即 $w^*,b^*=argmin_{w,b}L(w,b)$

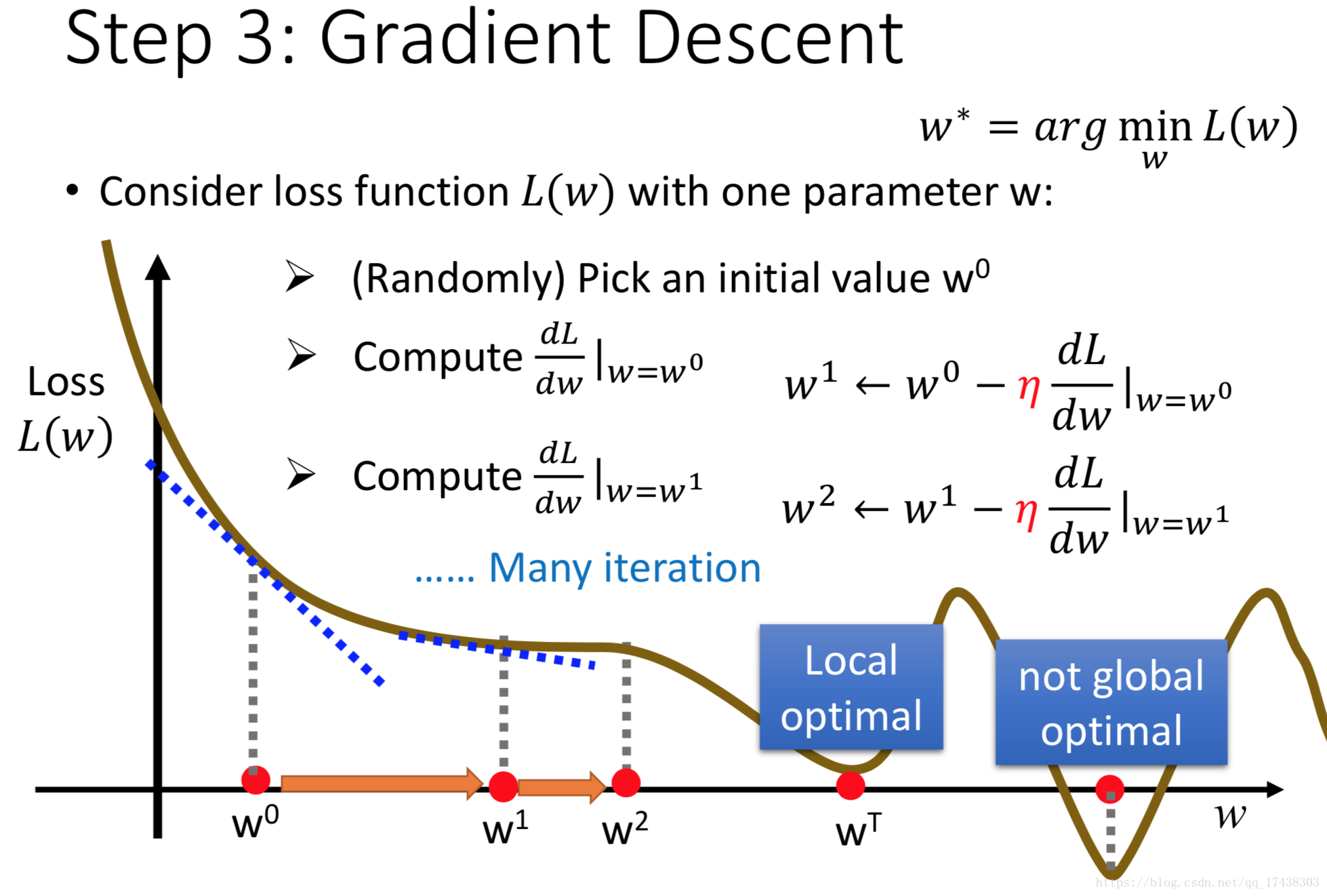
求L函数最小值问题一般用梯度下降法来进行计算，步骤如下：

随机初始化 $w^0,b^0$
计算 $L(w,b)$ 函数在 $w^0,b^0$ 处的偏导 $\frac{dL}{dw}|_{w=w^0},\frac{dL}{db}|_{b=b^0}$ ， $w^1:=w^0-\eta \frac{dL}{dw}|_{w=w^0},b^1:=b^0-\eta \frac{dL}{db}|_{b=b^0},$ ，其中 $\eta$ 为学习速率（Learning rate）
重复第二步直到 $w,b$ 收敛

注意：梯度下降方法可能得到的是局部最优，在线性回归模型中， $L(w,b)$ 函数是凸的，因此梯度下降得到的最优解即全局最优解

使用梯度下降算法求解案例最小化问题，

$minL(w,b)=min\sum_{n=1}^{10}(\hat{y}^n-(b+wx_{cp}^n))^2$

$\frac{\partial L}{\partial w}=\sum_{n=1}^{10}2(\hat{y}^n-(b+wx_{cp}^n))(-x_{cp}^n),\frac{\partial L}{\partial b}=\sum_{n=1}^{10}2(\hat{y}^n-(b+wx_{cp}^n))(-1)$

$e^n=\hat{y}^n-f^*(x_{cp}^n),n=1,2\dots10$ ，表示训练集中第n个观测的误差，使用新捕捉的10只宝可梦作为测试集计算平均误差，以此来评价模型的泛化能力，现在我们考虑更复杂的线性模型，即在Step1中的 $f$ 不再仅仅使用 $x_{cp}$ 的一次变量。（tips：模型的总误差可以从bias和variance两方面考虑，bias衡量训练集的拟合效果，variance衡量测试集结果的稳定性）

Model	Best Function	训练集平均误差	测试集平均误差
$y=b+wx_{cp}$	$b = -188.4,w = 2.7$	35.0	31.9
$y=b+w_1x_{cp}+w_2x_{cp}^2$	$b = -10.3,w_1 = 1.0, w_2 = 2.7*10^{-3}$	15.4	18.4
$y=b+w_1x_{cp}+w_2x_{cp}^2+w_3x_{cp}^3$	$b = 6.4, w_1 = 0.66 ,w_2 = 4.3 * 10^{-3},w_3 = -1.8 *10^{-6}$	15.3	18.1
$y=b+w_1x_{cp}+w_2 x_{cp}^2+w_3 x_{cp}^3+ w_4 x_{cp}^4$	$\dots\dots\dots$	14.9	28.8
$y=b+w_1x_{cp}+w_2 x_{cp}^2+w_3 x_{cp}^3+ w_4 x_{cp}^4+w_5 x_{cp}^5$	$\dots\dots\dots$	12.8	232.1

当模型越复杂，训练集平均误差越低，如图可以直观地理解，在越复杂的模型（对应越大的集合）找到的best function拟合效果显然越好，但是测试集平均误差并不是单调递减，在引入4次、5次项之后反而急剧增大，此时产生了过拟合问题（可以尝试增加训练集样本来解决）。

现在我们考虑更复杂的线性模型，即在Step1中的 $f$ 不再仅仅使用 $x_{cp}$ 的这一变量，引入 $x_s$ 变量（宝可梦种族），此时训练集平均误差为3.8，测试集平均误差为14.3，模型拟合与泛化效果都增强，在此基础上考虑变量的二次项，

此时模型过拟合，使用正则化方法来解决过拟合问题，即使Step2中的loss function 不仅仅考虑error，还考虑了参数个数， $L = \sum(\hat{y}^n-(b+\sum wx_{cp}^n))^2+\lambda \sum (w_i)^2$ ，此时我们假设平滑的 $f$ 更接近真正的 $f^*$ 。

为了兼顾最小化第二项，训练集平均误差相对于没有正则化的方法高，但是测试集平均误差降低，大大减少了过拟合的影响。

demo

# 进化前后CP值数据
x_data=[338.,333.,328.,207.,226.,25.,179.,60.,200.,606.]
y_data=[640.,633.,619.,393.,428.,27.,193.,66.,226.,1591.]

#假设模型
#y_data = b + w*x_data

#初始化w、b
w,b = -4,-120
#学习速率
lr = 0.000001
#迭代次数
iter = 100000

b_history=[b]
w_history=[w]

for i in range(iter):
    b_grad = 0.0
    w_grad = 0.0
    for n in range(len(x_data)):
        b_grad -= 2.0*(y_data[n] - b*w*x_data[n])*1.0
        w_grad -= 2.0*(y_data[n] - b*w*x_data[n])*x_data[n]
    #更新参数
    b = b -lr*b_grad
    w = w -lr*w_grad
    #储存w、b
    b_history.append(b)
    w_history.append(w)

可视化结果如下，纵轴代表w的变化，横轴代表b的变化，我们发现参数的最终结果里最佳点（黄色叉号）仍然非常遥远，考虑增大学习速率，并使用Adagrad方法设置学习速率。

课程视频来源点击我

1、Regression - Case Study（回归-案例分析）

Objective

step1：Model

step2：Goodness of Function

step3：Best Function

demo

猜你喜欢