机器人位置运动学03—D-H参数法

一、关节与连杆

　　机器人一般由一系列关节和连杆按任意的顺序连接而成，这些关节可能是滑动（线性）的或旋转（转动）的，它们可能处在不同的平面，旋转轴之间可能存在偏差。连杆也可以是任意长度的（包括零），它可能被扭曲或弯曲，也可能位于任意的平面上。所以任何一组关节和连杆都可以构成机器人。我们必须要能对任何机器人进行建模和分析。
　　所以，我们需要给每个关节指定一个参考坐标系，然后确定从一个关节到下一个关节（一个坐标系到下一个坐标系）进行变换的步骤。如果将从基座到第1关节，再从第1关节到第2关节直至最后一个关节的所有变换结合起来，就得到了机器人的总变换矩阵。
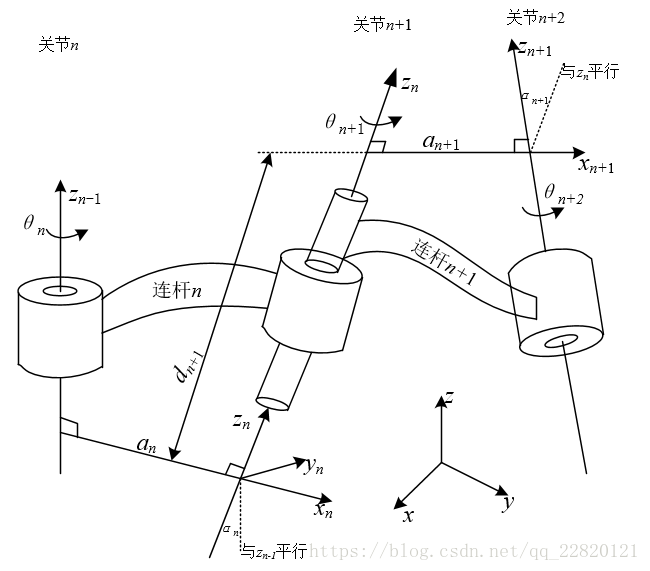
　　假设机器人由任意多的连杆和关节以任意形式构成，如图所示，有3个顺序的关节和2个连杆，每个关节都可能是旋转的、滑动的或两者都是。指定第1个关节为关节 $n$ ，第2个关节为关节 $n+1$ ，第3个关节为关节 $n+2$ 。连杆 $n$ 位于关节 $n$ 与 $n+1$ 之间，连杆 $n+1$ 位于关节 $n+1$ 与 $n+2$ 之间。
　　

二、D-H参数法中 $x,y,z$ 轴及参数说明

　　为了用D-H表示法对机器人建模，所要做的第一件事是为每个关节指定一个本地的参考坐标系。因此，对于每个关节，都必须指定一个 $z$ 轴和 $x$ 轴，通常并不需要指定 $y$ 轴，因为 $y$ 轴总是垂直于 $x$ 轴和 $z$ 轴。

$z$ 轴：所有关节，无一例外都用 $z$ 轴表示。如果关节是旋转的，那么 $z$ 轴位于按右手规则旋转的方向。如果关节是滑动的，那么 $z$ 轴为沿直线运动的方向。绕关节 $n+1$ 运动的 $z$ 轴是 $z_n$ 。对于旋转关节，绕 $z$ 轴的旋转角 $\theta$ 是关节变量。对于滑动关节，沿 $z$ 轴的连杆长度 $d$ 是关节变量。
$x$ 轴：通常关节不一定平行或相交。因此， $z$ 轴也许是斜线，但总有一条距离最短的公垂线，它正交于任意两条斜线。通常在公垂线方向上定义本地参考坐标系的 $x$ 轴。所以如果 $a_n$ 表示 $z_n-1$ 与 $z_n$ 之间的公垂线，则定义 $x_n$ 的方向为沿 $a_n$ 的方向。
特殊情况：
(1)：如果两个关节的 $z$ 轴平行，那么它们之间就有无数条公垂线。这时可挑选与前一关节的公垂线共线的一条公垂线。
(2)：如果两个相邻关节的 $z$ 轴是相交的，那么它们之间就没有公垂线（或者公垂线的距离为零）。这时可将垂直于两条轴线构成的平面的直线指定为 $x$ 轴，即其公垂线是垂直于包含了两条 $z$ 轴平面的直线。
$\theta$ ：表示绕 $z$ 轴的旋转角
$d$ ：表示在 $z$ 轴上两条相邻的公垂线之前的距离（关节偏移）
$a$ ：表示每一条公垂线的长度（连杆长度）
$\alpha$ ：表示两个相邻的 $z$ 轴之间的角度（扭角）
通常只有 $\theta$ 和 $d$ 是关节变量。

三、D-H参数法的坐标变换矩阵

　　现在需要将一个参考坐标系变换到下一个参考坐标系。假设现在位于本地参考坐标系 $x_n-z_n$ ，则通过以下4步标准运动即可到达下一个本地参考坐标系 $x_{n+1}-z_{n+1}$ 。
　　(1)绕 $z_n$ 轴旋转 $\theta_{n+1}$ ，使得 $x_n$ 和 $x_{n+1}$ 互相平行。因为 $a_n$ 和 $a_{n+1}$ 都是垂直于 $z_n$ 轴的，因此绕 $z_n$ 轴旋转 $\theta_{n+1}$ 确实可使 $x_n$ 和 $x_{n+1}$ 平行（且共面）。
　　(2)沿 $z_n$ 轴平移 $d_{n+1}$ 距离，使得 $x_n$ 和 $x_{n+1}$ 共线。因为 $x_n$ 和 $x_{n+1}$ 已经平行且垂直于 $z_n$ ，则沿着 $z_n$ 移动可使它们相互重叠在一起。
　　(3)沿已经旋转过的 $x_n$ 轴平移 $a_{n+1}$ 的距离，使得 $x_n$ 和 $x_{n+1}$ 的原点重合。这时两个参考坐标系的原点处在同一位置。
　　(4)将 $z$ 轴绕 $x_{n+1}$ 轴旋转 $\alpha_{n+1}$ ，使得 $z_n$ 轴与 $z_{n+1}$ 轴对准。这时坐标系 $n$ 和 $n+1$ 完全相同。这样就实现了从一个坐标系变换到下一个坐标系。
　　在坐标系 $n+1$ 和 $n+2$ 之间，严格地按照上述的4个步骤就可以将一个坐标系变换到下一个坐标系。通过重复以上步骤，可以实现一系列相邻坐标系之间的变换。从机器人的参考坐标系开始，我们可以将其转换到机器人的第1个关节，在转换到第2个关节，以此类推，直至转换到末端执行器。
　　表示前面4个运动的两个依次坐标系之间的变换 $^nT_{n+1}$ （称为 $A_{n+1}$ ）是4个运动变换矩阵的乘积。由于所有的变换都是相对于当前的坐标系进行的，因此所有的变换都是右乘的。即
　　

^{n} T_{n + 1} = A_{n + 1} = R o t (z, θ_{n + 1}) \times T r a n s (0, 0, d_{n + 1}) \times T r a n s (a_{n + 1}, 0, 0) \times R o t (x, α_{n + 1})

$^nT_{n+1}=A_{n+1}=Rot(z,\theta_{n+1})\times Trans(0,0,d_{n+1})\times Trans(a_{n+1},0,0)\times Rot(x,\alpha_{n+1})$
　

= [\begin{matrix} c o s θ_{n + 1} & - s i n θ_{n + 1} & 0 & 0 \\ s i n θ_{n + 1} & c o s θ_{n + 1} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] \times [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & d_{n + 1} \\ 0 & 0 & 0 & 1 \end{matrix}] \times [\begin{matrix} 1 & 0 & 0 & a_{n + 1} \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] \times [\begin{matrix} 1 & 0 & 0 & 0 \\ 0 & c o s α_{n + 1} & - s i n α_{n + 1} & 0 \\ 0 & s i n α_{n + 1} & c o s α_{n + 1} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$=\left[ \begin{matrix} cos\theta_{n+1}&-sin\theta_{n+1} & 0 &0 \\ sin\theta_{n+1} & cos\theta_{n+1} &0&0 \\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] \times \left[ \begin{matrix} 1&0 & 0 &0 \\ 0& 1 &0&0 \\ 0 & 0 & 1 &d_{n+1}\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] \times \left[ \begin{matrix} 1&0 & 0 &a_{n+1} \\ 0& 1 &0&0 \\ 0 & 0 & 1 &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]\times \left[ \begin{matrix} 1&0 & 0 &0 \\ 0& cos\alpha_{n+1} &-sin\alpha_{n+1}&0 \\ 0 & sin\alpha_{n+1} & cos\alpha_{n+1} &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$

A_{n + 1} = [\begin{matrix} c o s θ_{n + 1} & - s i n θ_{n + 1} c o s α_{n + 1} & s i n θ_{n + 1} s i n α_{n + 1} & a_{n + 1} c o s θ_{n + 1} \\ s i n θ_{n + 1} & c o s θ_{n + 1} c o s α_{n + 1} & - c o s θ_{n + 1} s i n α_{n + 1} & a_{n + 1} s i n θ_{n + 1} \\ 0 & s i n α_{n + 1} & c o s α_{n + 1} & d_{n + 1} \\ 0 & 0 & 0 & 1 \end{matrix}]

$A_{n+1}=\left[ \begin{matrix} cos\theta_{n+1}&-sin\theta_{n+1}cos\alpha_{n+1}&sin\theta_{n+1}sin\alpha_{n+1} &a_{n+1}cos\theta_{n+1} \\ sin\theta_{n+1}& cos\theta_{n+1}cos\alpha_{n+1} &-cos\theta_{n+1}sin\alpha_{n+1}&a_{n+1}sin\theta_{n+1} \\ 0 & sin\alpha_{n+1} & cos\alpha_{n+1} &d_{n+1}\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$
　　在机器人基座上，可以从第1个关节开始变换到第2个关节，然后到第3个关节等等，直到机器人手和最终的末端执行器。若把每个变换定义为

A_{n + 1}

$A_{n+1}$ ，则可以得到许多表示变换的

A

$A$ 矩阵。在机器人的基座与手之间的总变换则为：
　　

^{R} T_{H} =^{R} T_{1}^{1} T_{2}^{2} T_{3} . . .^{n - 1} T_{n} = A_{1} A_{2} A_{3} . . . A_{n}

$^RT_H=^RT_1^1T_2^2T_3...^{n-1}T_n=A_1A_2A_3...A_n$
　　其中

n

$n$ 是关节数，有几个自由度就有几个

A

$A$ 矩阵。通常可以制作一张关节和连杆参数的表格，其中每个连杆和关节的参数值可从机器人的机构示意图上确定。

连杆	$\theta$	$d$	$a$	$\alpha$
0-1
1-2

四、正运动学例题

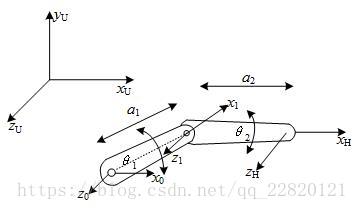
例1：如图所示的简单2轴平面机器人，根据D-H表示法，建立必要的坐标系，填写D-H参数表，导出每个机器人的正运动学方程。

解：首先两个关节都在 $x-y$ 平面内旋转，坐标系 $x_H-z_H$ 表示机器人的末端。先指定关节的 $z$ 轴，将关节1指定为 $z_0$ ，关节2指定为 $z_1$ ，坐标系0是固定不动的，机器人相对于它而运动。
　　然后为每一个坐标系指定 $x$ 轴，因为第1个坐标系（坐标系0）是在机器人基座上，在它之前没有关节，因此 $x_0$ 的方向是任意的。我们可以指定 $x_0$ 的方向与全局坐标系的 $x$ 轴相同。因为 $z_0$ 和 $z_1$ 是平行的，他们之间的公垂线就在两者之间的方向上，所以 $x_1$ 轴如图所示。
　　下表显示了该机器人的变量表。根据D-H的常规步骤，按照如下从一个坐标系到下一个坐标系所必须的4个变换，可以来确认变量表中的这些值。

连杆	$\theta$	$d$	$a$	$\alpha$
0-1	$\theta_1$	0	$a_1$	0
1- $H$	$\theta_2$	0	$a_2$	0

　　(1)绕 $z_0$ 轴旋转 $\theta_1$ ，使 $x_0$ 和 $x_1$ 平行；
　　(2)由于 $x_0$ 和 $x_1$ 已经在一个平面内了，不需要在平移 $z_0$ 轴，因此沿着 $z_0$ 轴的偏移量 $d$ 是0；
　　(3)沿着已经旋转过的 $x_0$ 轴平移距离 $a_1$ ；
　　(4)因为 $z_0$ 和 $z_1$ 是平行的，不需要在旋转，因此绕 $x_1$ 轴的旋转角 $\alpha_1$ 是0。
　　坐标系1到坐标系 $H$ 之间的变换与上面的过程类似。
　　由于有两个旋转关节，因此存在两个未知的变量，即关节角 $\theta_1$ 和 $\theta_2$ 。将D-H参数表中的这些参数代入相应的A矩阵中，可以得到机器人的正运动学方程为：
　　

A_{1} = [\begin{matrix} c o s θ_{1} & - s i n θ_{1} & 0 & a_{1} c o s θ_{1} \\ s i n θ_{1} & c o s θ_{1} & 0 & a_{1} s i n θ_{1} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}], A_{2} = [\begin{matrix} c o s θ_{2} & - s i n θ_{2} & 0 & a_{2} c o s θ_{2} \\ s i n θ_{2} & c o s θ_{2} & 0 & a_{2} s i n θ_{2} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$A_1= \left[ \begin{matrix} cos\theta_1&-sin\theta_1 & 0 &a_1cos\theta_1 \\ sin\theta_1&cos\theta_1 &0&a_1sin\theta_1 \\ 0 & 0 &1 &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] ,　 A_2= \left[ \begin{matrix} cos\theta_2&-sin\theta_2 & 0 &a_2cos\theta_2 \\ sin\theta_2&cos\theta_2 &0&a_2sin\theta_2 \\ 0 & 0 &1 &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$
　　

^{0} T_{H} = A_{1} \times A_{1} = [\begin{matrix} c o s (θ_{1} + θ_{2}) & - s i n (θ_{1} + θ_{2}) & 0 & a_{2} c o s (θ_{1} + θ_{2}) + a_{1} c o s θ_{1} \\ s i n (θ_{1} + θ_{2}) & c o s (θ_{1} + θ_{2}) & 0 & a_{2} s i n (θ_{1} + θ_{2}) + a_{1} s i n θ_{1} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$^0T_H=A_1\times A_1= \left[ \begin{matrix} cos(\theta_1+\theta_2)&-sin(\theta_1+\theta_2) & 0 &a_2cos(\theta_1+\theta_2)+a_1cos\theta_1\\ sin(\theta_1+\theta_2)&cos(\theta_1+\theta_2)&0&a_2sin(\theta_1+\theta_2)+a_1sin\theta_1 \\ 0 & 0 &1 &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$
　　给定

θ_{1} 、 θ_{2} 、 a_{1}

$\theta_1、\theta_2、a_1$ 和

a_{2}

$a_2$ ，根据正运动学方程就可以求出机器人末端的位置和姿态。

五、逆运动学例题

　　有了逆运动学解才能确定每个关节的值，从而使机器人到达期望的位姿。
例2：求解例1中的关节角。
解1：设期望的位置和姿态为：

扫描二维码关注公众号，回复： 2254523 查看本文章

^{0} T_{H} = A_{1} \times A_{1} = [\begin{matrix} c o s (θ_{1} + θ_{2}) & - s i n (θ_{1} + θ_{2}) & 0 & a_{2} c o s (θ_{1} + θ_{2}) + a_{1} c o s θ_{1} \\ s i n (θ_{1} + θ_{2}) & c o s (θ_{1} + θ_{2}) & 0 & a_{2} s i n (θ_{1} + θ_{2}) + a_{1} s i n θ_{1} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] = [\begin{matrix} n_{x} & o_{x} & a_{x} & p_{x} \\ n_{y} & o_{y} & a_{y} & p_{y} \\ n_{z} & o_{z} & a_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]

s i n (θ_{1} + θ_{2}) = n_{y}

$sin(\theta_1+\theta_2) = n_y$ 且

c o s (θ_{1} + θ_{2}) = n_{x}

$cos(\theta_1+\theta_2) = n_x$ ，所以：

θ_{1} + θ_{2} = A T A N 2 (n_{y}, n_{x})

$\theta_1+\theta_2=ATAN2(n_y,n_x)$ 。
又因为

a_{2} c o s (θ_{1} + θ_{2}) + a_{1} c o s θ_{1} = p_{x} \Rightarrow a_{2} n_{x} + a_{1} c o s θ_{1} = p_{x}

$a_2cos(\theta_1+\theta_2)+a_1cos\theta_1=p_x\Rightarrow a_2n_x+a_1cos\theta_1=p_x$ ，所以：

c o s θ_{1} = \frac{p_{x} - a_{2} n_{x}}{a_{1}}

$cos\theta_1=\frac{p_x-a_2n_x}{a_1}$ 。
又因为

a_{2} s i n (θ_{1} + θ_{2}) + a_{1} s i n θ_{1} = p_{y} \Rightarrow a_{2} n_{y} + a_{1} s i n θ_{1} = p_{y}

$a_2sin(\theta_1+\theta_2)+a_1sin\theta_1=p_y\Rightarrow a_2n_y+a_1sin\theta_1=p_y$ ，所以：

s i n θ_{1} = \frac{p_{x} - a_{2} n_{x}}{a_{1}}

$sin\theta_1=\frac{p_x-a_2n_x}{a_1}$ 。
所以：

θ_{1} = A T A N 2 (s i n θ_{1}, c o s θ_{1}) = A T A N 2 (\frac{p_{x} - a_{2} n_{x}}{a_{1}}, \frac{p_{x} - a_{2} n_{x}}{a_{1}})

$\theta_1=ATAN2(sin\theta_1,cos\theta_1)=ATAN2(\frac{p_x-a_2n_x}{a_1},\frac{p_x-a_2n_x}{a_1})$ 。所以

θ_{2} = θ_{1} + θ_{2} - θ_{1}

$\theta_2 = \theta_1+\theta_2-\theta_1$ 。
解2：在等式中通常乘

A_{2}^{- 1}

$A_{2}^{-1}$ ，使得

θ_{1}

$\theta_1$ 从

θ_{2}

$\theta_2$ 中解耦。（常用于多自由度的）

A_{1} \times A_{2} \times A_{2}^{- 1} = [\begin{matrix} n_{x} & o_{x} & a_{x} & p_{x} \\ n_{y} & o_{y} & a_{y} & p_{y} \\ n_{z} & o_{z} & a_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] \times A_{2}^{- 1} \Rightarrow A_{1} = [\begin{matrix} n_{x} & o_{x} & a_{x} & p_{x} \\ n_{y} & o_{y} & a_{y} & p_{y} \\ n_{z} & o_{z} & a_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] \times A_{2}^{- 1}

$A_1\times A_2 \times A_{2}^{-1}= \left[ \begin{matrix} n_x&o_x & a_x &p_x\\ n_y&o_y & a_y &p_y\\ n_z&o_z & a_z&p_z\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] \times A_2^{-1} \Rightarrow A_1= \left[ \begin{matrix} n_x&o_x & a_x &p_x\\ n_y&o_y & a_y &p_y\\ n_z&o_z & a_z&p_z\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] \times A_2^{-1}$

[\begin{matrix} c o s θ_{1} & - s i n θ_{1} & 0 & a_{1} c o s θ_{1} \\ s i n θ_{1} & c o s θ_{1} & 0 & a_{1} s i n θ_{1} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] = [\begin{matrix} n_{x} & o_{x} & a_{x} & p_{x} \\ n_{y} & o_{y} & a_{y} & p_{y} \\ n_{z} & o_{z} & a_{z} & p_{z} \\ 0 & 0 & 0 & 1 \end{matrix}] \times [\begin{matrix} c o s θ_{2} & - s i n θ_{2} & 0 & - a_{2} \\ s i n θ_{2} & c o s θ_{2} & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}]

$\left[ \begin{matrix} cos\theta_1&-sin\theta_1 & 0 &a_1cos\theta_1 \\ sin\theta_1&cos\theta_1 &0&a_1sin\theta_1 \\ 0 & 0 &1 &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] = \left[ \begin{matrix} n_x&o_x & a_x &p_x\\ n_y&o_y & a_y &p_y\\ n_z&o_z & a_z&p_z\\ 0 & 0 & 0 & 1\\ \end{matrix} \right] \times \left[ \begin{matrix} cos\theta_2&-sin\theta_2 & 0& -a_2\\ sin\theta_2&cos\theta_2 & 0 &0\\ 0 & 0 & 1 &0 \\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$

[\begin{matrix} c o s θ_{1} & - s i n θ_{1} & 0 & a_{1} c o s θ_{1} \\ s i n θ_{1} & c o s θ_{1} & 0 & a_{1} s i n θ_{1} \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] = [\begin{matrix} c o s θ_{2} n_{x} - s i n θ_{2} o_{x} & s i n θ_{2} n_{x} + c o s θ_{2} o_{x} & a_{x} & p_{x} - a_{2} n_{x} \\ c o s θ_{2} n_{y} - s i n θ_{2} o_{y} & s i n θ_{2} n_{y} + c o s θ_{2} o_{y} & a_{y} & p_{y} - a_{2} n_{y} \\ c o s θ_{2} n_{z} - s i n θ_{2} o_{z} & s i n θ_{2} n_{z} + c o s θ_{2} o_{z} & a_{z} & p_{z} - a_{2} n_{z} \\ 0 & 0 & 0 & 1 \end{matrix}]

$\left[ \begin{matrix} cos\theta_1&-sin\theta_1 & 0 &a_1cos\theta_1 \\ sin\theta_1&cos\theta_1 &0&a_1sin\theta_1 \\ 0 & 0 &1 &0\\ 0 & 0 & 0 & 1\\ \end{matrix} \right]= \left[ \begin{matrix} cos\theta_2n_x-sin\theta_2o_x&sin\theta_2n_x+cos\theta_2o_x &a_x &p_x-a_2n_x \\ cos\theta_2n_y-sin\theta_2o_y&sin\theta_2n_y+cos\theta_2o_y &a_y &p_y-a_2n_y \\ cos\theta_2n_z-sin\theta_2o_z&sin\theta_2n_z+cos\theta_2o_z &a_z &p_z-a_2n_z \\ 0 & 0 & 0 & 1\\ \end{matrix} \right]$
对应位置矩阵元素相等即可求得

θ_{1}

$\theta_1$ 和

θ_{2}

$\theta_2$ ，其结果和解1一样。

参考文献：SaeedB.Niku 等，机器人学导论——分析、系统及应用（第二版），电子工业出版社，2013.2.