线性回归

本博客为博主查阅大量资料后整理原创，虽水仍不易，如需转载，请附上本文链接https://blog.csdn.net/JasonLeeeeeeeeee/article/details/81019399，谢谢
本文若有不足之处可以交流沟通，互相学习

1. 介绍

在吴恩达大神的机器学习视频中，线性回归是第一块讲的内容，是以房价为例进行讲解。房价跟面积、地理位置等因素相关，具体呈现怎样的相关性，每个因素占多大的比重，这就是线性回归的主要功能了。我们在知道答案和各个影响因素的前提下，来训练学习每个因素在影响最终结果的比重，即每个因素之前的系数。在统计学中，线性回归（Linear Regression）是利用称为线性回归方程的最小平方函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合（自变量都是一次方）。只有一个自变量的情况称为简单回归，大于一个自变量情况的叫做多元回归。

优点：结果易于理解，计算上不复杂。
缺点：对非线性数据拟合不好。
适用数据类型：数值型和标称型数据。

2. 模型推导

假设：
1. 输入的X和Y满足线性关系，通过训练可以建立机器学习模型，即输入的Y和X之间满足方程 $Y=\theta^TX+e$ 其中 $e$ 是误差项，噪音项；
2. 最终训练出来的线性模型为 $h_\theta(x)=\theta^TX$ ；
3. 使用表示数据组数，使用表示数据的维数；
4. 训练样本的数据量很大的时候,根据中心极限定律可以得到 $\sum e$ 满足 $(u,\sigma^2)$ 高斯分布的，由于方程有截距项，故满足 $(0,\sigma^2)$ 的高斯分布，即 $h_\theta(x)-y^i \backsim N(0,\sigma^2) \quad i = 1\ to \ m$ .

我们可以得到似然函数为：

L (y | x; θ) = \prod_{i = 1}^{m} P (y^{i} | x^{i}; θ) = \prod_{i = 1}^{m} N (h_{θ} (x^{i}) - y^{i}; 0, σ^{2})

$L(y|x;\theta)=\prod^m_{i=1}P(y^i|x^i;\theta)=\prod^m_{i=1}N(h_\theta(x^i)-y^i;0,\sigma^2)$
两边取对数可得：

l n L (y | x; θ) = \sum_{i = 1}^{m} l n N (h_{θ} (x^{i}) - y^{i}; 0, σ^{2}) = \sum_{i = 1}^{m} l n (\frac{1}{\sqrt{2 π} σ} e x p (- \frac{1}{2 σ^{2}} (h_{θ} (x^{i}) - y^{i})^{2}))

$ln\ L(y|x;\theta)=\sum^m_{i=1}ln\ N(h_\theta(x^i)-y^i;0,\sigma^2)=\sum^m_{i=1}ln\ (\frac{1}{\sqrt{2\pi}\sigma}exp(-\frac{1}{2\sigma^2}(h_\theta(x^i)-y^i)^2))$

= \sum_{i = 1}^{m} l n (\frac{1}{\sqrt{2 π} σ}) - \sum_{i = 1}^{m} \frac{1}{2 σ^{2}} (h_{θ} (x^{i}) - y^{i})^{2} = - m l n (\sqrt{2 π} σ) - \frac{1}{2 σ^{2}} \sum_{i = 1}^{m} (h_{θ} (x^{i}) - y^{i})^{2}

$=\sum^m_{i=1}ln\ (\frac{1}{\sqrt{2\pi}\sigma})-\sum^m_{i=1}\frac{1}{2\sigma^2}(h_\theta(x^i)-y^i)^2=-mln\ (\sqrt{2\pi}\sigma)-\frac{1}{2\sigma^2}\sum^m_{i=1}(h_\theta(x^i)-y^i)^2$
定义损失函数为：

J (θ) = \frac{1}{2 m} \sum_{i = 1}^{m} (h_{θ} (x^{i}) - y^{i})^{2}

$J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^i)-y^i)^2$
损失函数极小值代替最小值，可以得到似然函数最大值，有两种方法：
1. 使用矩阵求

θ

$\theta$ ：

J (θ) = \frac{1}{2} (θ X - Y)^{T} (θ X - Y) = \frac{1}{2} [θ^{T} X^{T} X θ - W^{T} X^{T} Y - Y^{T} X θ + Y^{T} Y] = \frac{1}{2} [θ^{T} X^{T} X θ - 2 θ^{T} X^{T} Y + Y^{T} Y]

$J(\theta)=\frac{1}{2}(\theta X-Y)^T(\theta X-Y)=\frac{1}{2}[\theta^TX^TX\theta-W^TX^TY-Y^TX\theta+Y^TY]=\frac{1}{2}[\theta^TX^TX\theta-2\theta^TX^TY+Y^TY]$

\frac{\partial J (θ)}{θ} = \frac{1}{2} [θ^{T} X^{T} X - 2 X^{T} Y] = 0

$\frac{\partial J(\theta)}{\theta}=\frac{1}{2}[\theta^TX^TX-2 X^TY]=0$

θ = (X^{T} X)^{- 1} X^{T} Y

$\theta=(X^TX)^{-1}X^TY$
该方法有一个局限性就是要求矩阵可逆；
2. 梯度下降法求

θ

$\theta$ ：
通过沿着负梯度方向进行迭代，更新后的

θ

$\theta$ 使

J (θ)

$J(\theta)$ 更小.

θ = θ - α \frac{\partial J (θ)}{\partial θ} α 为 学 习 率 、 步 长

$\theta=\theta-\alpha\frac{\partial J(\theta)}{\partial\theta}\quad \alpha为学习率、步长$

J (θ)

$J(\theta)$ 两边对

θ_{j}

$\theta_j$ 求偏导为：

\frac{\partial}{\partial θ_{j}} J (θ) = \frac{1}{m} \sum_{i = 1}^{m} (h_{θ} (x^{i}) - y^{i}) x_{j}^{i} j = 0 t o n

$\frac {\partial}{\partial\theta_j}J(\theta)=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^i)-y^i)x^i_j\quad j=0\ to\ n$

梯度下降

在进行梯度下降计算 $\theta$ 时，最常见的有三种变形BGD，SGD，MBGD，这三种形式的主要区别为我们用多少数据来进行计算目标函数的梯度。
1. Batch Gradient Descent （BGD）批量梯度下降
BGD 采用整个训练集的数据来计算参数的梯度，缺点是由于这种方法是在一次更新中，就对整个数据集计算梯度，所以计算起来非常慢，遇到很大量的数据集也会非常棘手，而且不能投入新数据实时更新模型。

for i in range(nb_epochs):
  params_grad = evaluate_gradient(loss_function, data, params)
  params = params - learning_rate * params_grad

既然当数据量大的时候，计算速度较慢，那么我们可以选择其中的一部分数据进行计算，那么就引出了一下两种变形；
2. Stochastic Gradient Descent (SGD) 随机梯度下降
和 BGD 的一次用所有数据计算梯度相比，SGD 每次更新时对每个样本进行梯度更新，对于很大的数据集来说，可能会有相似的样本，这样 BGD 在计算梯度时会出现冗余，而 SGD 一次只进行一次更新，就没有冗余，而且比较快，并且可以新增样本。

for i in range(nb_epochs):
  np.random.shuffle(data)
  for example in data:
    params_grad = evaluate_gradient(loss_function, example, params)
    params = params - learning_rate * params_grad

该方法虽然训练速度快，但会由于受噪音的影响准确度下降，并不是全局最优。当然BGD可能收敛到局部最小值，SGD的震荡可能就跳到了更好的局部最小值。
3. Mini-Batch Gradient Descent （MBGD）小批量梯度下降
MBGD 每一次利用一小批样本，即 n 个样本进行计算，这样它可以降低参数更新时的方差，收敛更稳定，另一方面可以充分地利用深度学习库中高度优化的矩阵操作来进行更有效的梯度计算。和 SGD 的区别是每一次循环不是作用于每个样本，而是具有 n 个样本的批次。

for i in range(nb_epochs):
  np.random.shuffle(data)
  for batch in get_batches(data, batch_size=50):
    params_grad = evaluate_gradient(loss_function, batch, params)
    params = params - learning_rate * params_grad

缺点：（两大缺点）

1) 不过 Mini-batch gradient descent 不能保证很好的收敛性，learning rate 如果选择的太小，收敛速度会很慢，如果太大，loss function 就会在极小值处不停地震荡甚至偏离。（有一种措施是先设定大一点的学习率，当两次迭代之间的变化低于某个阈值后，就减小 learning rate，不过这个阈值的设定需要提前写好，这样的话就不能够适应数据集的特点。）对于非凸函数，还要避免陷于局部极小值处，或者鞍点处，因为鞍点周围的error是一样的，所有维度的梯度都接近于0，SGD 很容易被困在这里。（会在鞍点或者局部最小点震荡跳动，因为在此点处，如果是训练集全集带入即BGD，则优化会停止不动，如果是mini-batch或者SGD，每次找到的梯度都是不同的，就会发生震荡，来回跳动。）
2) SGD对所有参数更新时应用同样的 learning rate，如果我们的数据是稀疏的，我们更希望对出现频率低的特征进行大一点的更新。LR会随着更新的次数逐渐变小。

过拟合

到这里，我们可以获得优化的特征方程，然而训练的结果会恰当拟合，当然也会出现欠拟合或过拟合现象。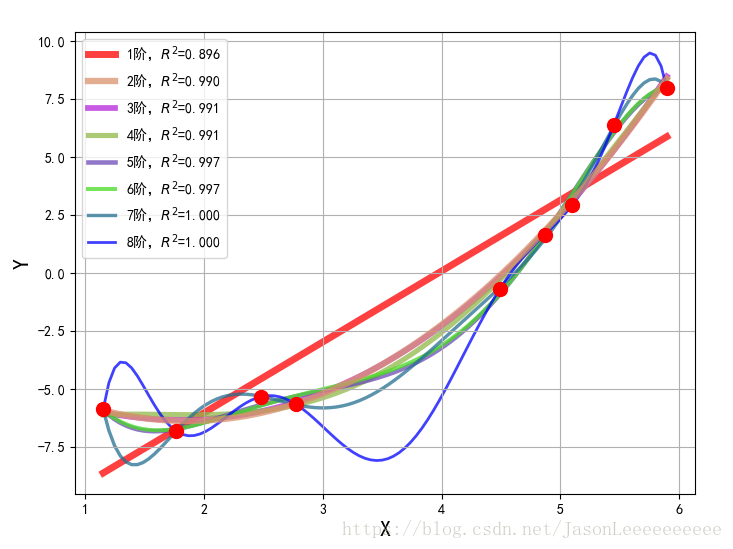示例图
例如上图中，当模型复杂度提高的时候，对训练集的数据拟合很好，但会出现过度拟合现象，为了防止这种过拟合现象的出现，通常解决过拟合问题的方法如下：
1.减少特征数量 ;
2.手动筛选特征;
3.增加样本量;
4.采用特征筛选算法;
5.正则化：保留所有的特征，但尽可能使参数 $\theta$ 尽量小.
正则化在很多特征变量对目标值只有很小影响的情况下非常有用。
我们在损失函数中加入了惩罚项，根据惩罚项不同分为以下：
L1范数是指向量中各个元素绝对值之和，也叫“稀疏规则算子”（Lasso regularization）。L2范数是指向量各元素的平方和然后求平方根，在回归里面，有人把有它的回归叫“岭回归”（Ridge Regression），有人也叫它“权值衰减”(weight decay)。
L1正则(Lasso回归)表达式如下：

J (θ) = \frac{1}{2 m} \sum_{i = 1}^{m} (h_{θ} (x^{i}) - y^{i})^{2} + λ \sum_{j = 1}^{n} | θ_{j} |

$J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^i)-y^i)^2+\lambda\sum^n_{j=1}|\theta_j|$
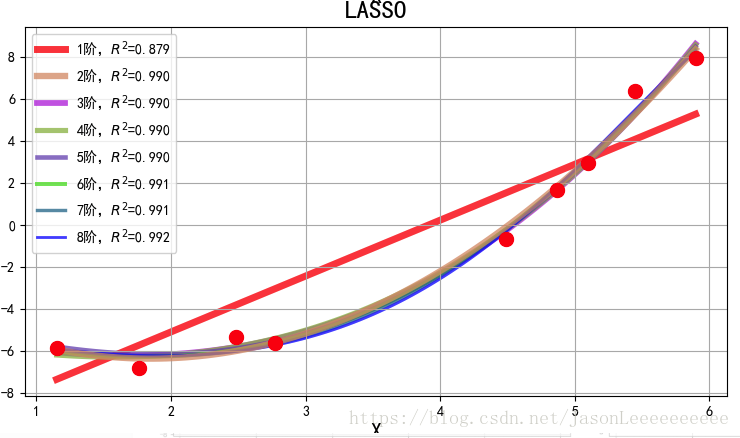
LASSO

L2正则(Ridge回归)表达式如下：

J (θ) = \frac{1}{2 m} \sum_{i = 1}^{m} (h_{θ} (x^{i}) - y^{i})^{2} + λ \sum_{j = 1}^{n} θ_{j}^{2}

$J(\theta)=\frac{1}{2m}\sum^m_{i=1}(h_\theta(x^i)-y^i)^2+\lambda\sum^n_{j=1}\theta^2_j$
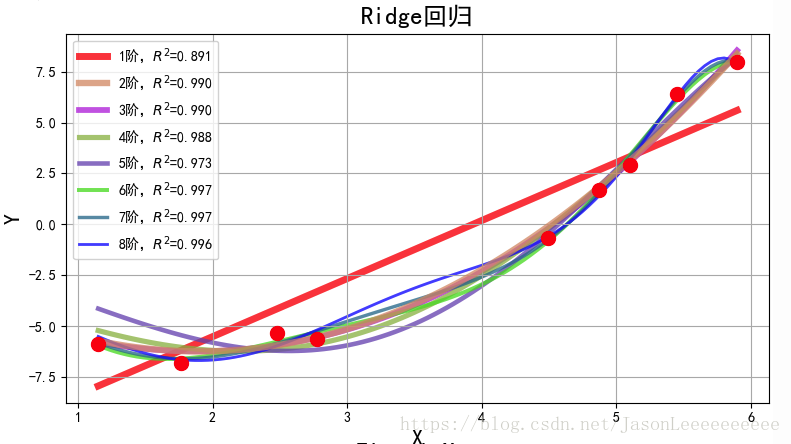
Ridge

L1和L2的直观感受
根据上述代价函数，可以写成以下形式
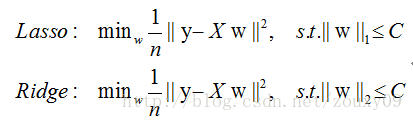
这里写图片描述

为了方便可视化，我们考虑二维空间，在平面上画出目标函数的等高线，而约束条件则成为平面上半径为C的一个 norm ball 。等高线与 norm ball 首次相交的地方就是最优解：
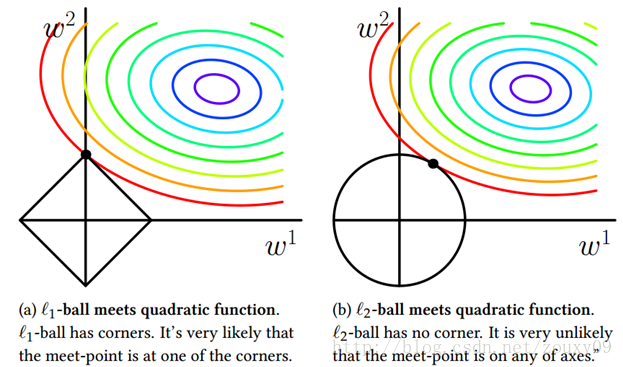
这里写图片描述

上图中可以看出L1第一次相交的点在w2上，则w1特征系数为0；同时，

λ

$\lambda$ 越大，则黑色方框越小，同理，

λ

$\lambda$ 越小，黑色方框越大。总结就是：L1会趋向于产生少量的特征，而其他的特征都是0，而L2会选择更多的特征，这些特征都会接近于0。Lasso在特征选择时候非常有用，而Ridge就只是一种规则化而已。
所以L1正则化会使某些特征系数为0，经常用于特征选择，可以在众多特征点中选择最相关的若干特征；L1正则化还具有可解释性，这跟之前的特性有所关联。因为之前会选择出几个最相关的数据特征，那么可以根据这几个特征进行解释，比方说在医院中，通过计算，可以得出来疾病与某些要素相关，如果说跟所提取大量的特征值都相关的话，病人肯定会难以接收。L2正则化呢，首先可以防止过拟合，提高模型泛化能力；从优化或者数值计算的角度来说，L2范数还有助于处理 condition number不好的情况下矩阵求逆很困难的问题。（优化有两大难题，一是：局部最小值，二是：ill-condition病态问题。condition number衡量的是输入发生微小变化的时候，输出会发生多大的变化。也就是系统对微小变化的敏感度。condition number值小的就是well-conditioned的，大的就是ill-conditioned的。这里解释更详细）
对于超参数

λ

$\lambda$ 的选择：L1范数中，越大的λ越容易使F(x)在x=0时取到最小值；L2范数中，λ越大，由梯度下降公式可得，

θ_{j}

$\theta_j$ 衰减得越快，L2圆的半径越小，最后求得代价函数最值时各参数也会变得很小。总之

λ

$\lambda$ 越大，就表示规则项要比模型训练误差越重要。

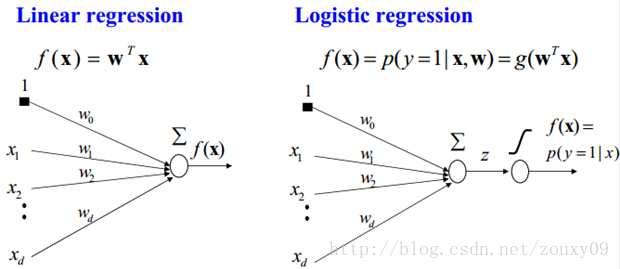
逻辑回归

逻辑回归是基于之前的线性回归增加了一个分类器函数，将离散游离的输出值规范到(0,1)范围内。线性回归是监督学习中的回归问题，在之后加一个分类器，就演变成了监督学习中的分类问题。线性回归与逻辑回归之间的关系可以参考下图：
这里写图片描述

1. sigmoid二分类器

sigmoid函数如下：

y = \frac{1}{1 + e^{- x}}

$y=\frac{1}{1+e^{-x}}$
该函数图像如下：
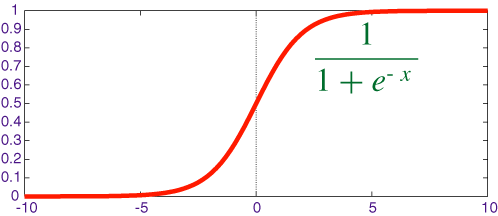
这里写图片描述

从图像中可以看出sigmoid函数的输出介于(0,1)之间，表明了数据属于某一类别的概率。将线性函数的结果映射到sigmoid函数中可得：

h_{θ} (x) = s i g m o i d (θ^{T} x) = \frac{1}{1 + e^{- θ^{T} x}}

$h_\theta(x)=sigmoid(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}}$

2. 模型推导

我们可以对输入x分类结果为1和0的概率分别表示为：

P (y = 1 | x; θ) = h_{θ} (x)

$P(y=1|x;\theta)=h_\theta(x)$

P (y = 0 | x; θ) = 1 - h_{θ} (x)

$P(y=0|x;\theta)=1-h_\theta(x)$
上述两式可以等价为：

P (y^{i} | x^{i}; θ) = (h_{θ} (x^{i}))^{y^{i}} (1 - h_{θ} (x^{i}))^{1 - y^{i}} f o r i = 1 t o m

$P(y^i|x^i;\theta)=(h_\theta(x^i))^{y^i}(1-h_\theta(x^i))^{1-y^i}\quad for\ i=1\ to\ m$
得到似然函数为：

L (y | x; θ) = \prod_{i = 1}^{m} P (y^{i} | x^{i}; θ) f o r i = 1 t o m

$L(y|x;\theta)=\prod^m_{i=1}P(y^i|x^i;\theta)\quad for\ i=1\ to\ m$
两边取对数可得：

l n L (y | x; θ) = \sum_{i = 1}^{m} l n P (y^{i} | x^{i}; θ) = \sum_{i = 1}^{m} (y^{i} l n h_{θ} (x^{i}) + (1 - y^{i}) l n (1 - h_{θ} (x^{i}))) f o r i = 1 t o m

$ln\ L(y|x;\theta)=\sum^m_{i=1}ln\ P(y^i|x^i;\theta)=\sum^m_{i=1}(y^iln\ h_\theta(x^i)+(1-y^i)ln\ (1-h_\theta(x^i)))\quad for\ i=1\ to\ m$
损失函数可以定义为：

J (θ) = - \frac{1}{m} \sum_{i = 1}^{m} (y^{i} l n h_{θ} (x^{i}) + (1 - y^{i}) l n (1 - h_{θ} (x^{i}))) f o r i = 1 t o m

$J(\theta)=-\frac{1}{m}\sum^m_{i=1}(y^iln\ h_\theta(x^i)+(1-y^i)ln\ (1-h_\theta(x^i)))\quad for\ i=1\ to\ m$
我们用梯度下降法进行计算

θ

$\theta$ ，需要要使似然函数最大，损失函数最小即可。我们用损失函数的极小值代替最小值，同时又因为sigmoid函数具有

\frac{d}{d z} s i g m o i d (z) = s i g m o i d (z) (1 - s i g m o i d (z))

$\frac{d}{dz}sigmoid(z)=sigmoid(z)(1-sigmoid(z))$ 的特性，可得：

\frac{\partial}{\partial θ_{j}} J (θ) = - \frac{1}{m} \sum_{i = 1}^{m} (\frac{y^{i}}{h_{θ} (x^{i})} - \frac{1 - y^{i}}{1 - h_{θ} (x^{i})}) h_{θ} (x^{i}) (1 - h_{θ} (x^{i})) x_{j}^{i} j = 0 t o n

$\frac{\partial}{\partial\theta_j}J(\theta)=-\frac{1}{m}\sum^m_{i=1}(\frac{y^i}{h_\theta(x^i)}-\frac{1-y^i}{1-h_\theta(x^i)})h_\theta(x^i)(1-h_\theta(x^i))x^i_j\quad j=0\ to\ n$

\frac{\partial}{\partial θ_{j}} J (θ) = \frac{1}{m} \sum_{i = 1}^{m} (h_{θ} (x^{i}) - y^{i}) x_{j}^{i} j = 0 t o n

$\frac{\partial}{\partial\theta_j}J(\theta)=\frac{1}{m}\sum^m_{i=1}(h_\theta(x^i)-y^i)x^i_j\quad j=0\ to\ n$
心细的同学应该能发现上式跟之前线性回归最后所求偏导结果一样，这不是巧了嘛！
之后的计算可以返回去再看上文中的梯度下降与过拟合两部分，都是一样的。

参考资料：
1. 统计学习方法李航
2. 机器学习周志华
2. https://blog.csdn.net/lc013/article/details/55002463
3. https://blog.csdn.net/July_sun/article/details/53223962
4. https://blog.csdn.net/lisi1129/article/details/68925799
5. https://www.cnblogs.com/guoyaohua/p/8780548.html
6. https://blog.csdn.net/vivian_ll/article/details/78580677
7. https://blog.csdn.net/programmer_wei/article/details/52072939

【机器学习】线性回归+逻辑回归（理论）

线性回归

1. 介绍

2. 模型推导

梯度下降

过拟合

逻辑回归

1. sigmoid二分类器

2. 模型推导

猜你喜欢