线性回归和逻辑回归在机器学习上是一种监督式学习。在预测类问题上,我们希望能通过一个映射关系 ,当给定变量
,能得到一个较为满意的预测结果
,回归方法旨在找到能表示样本空间分布的映射关系。
一、线性回归的基本形式
假设一个描述的示例: ,表示第
个样本具备
个特征。对于
个样本,每个样本都有
个特征,线性模型试图建立预测函数:
写成向量的形式:
,使得
二、线性回归的代价函数
为了能满足 ,问题转变成如何确立参数
和
,这点需要从预测值
与真实值
差距入手,因此需要引入代价函数来反映这种差距。这里使用均方误差函数:
三、正规方程求解线性回归
上述方程是针对第 个样本。对于
个样本, 每个样本
个特征。同时为了统一格式,需要加入
的情况,令
,写成矩阵形式:
,
令 ,整个问题转变成:
很自然的想到通过求导的方式来寻找最小值。对 求导并令导数为零,则有:
观察上式的 ,当
不可逆时(说明
的某些特征存在冗余,即某些特征线性相关),无法求得该关系式的逆。这时候需要引入正则化。同样地,当矩阵
规模过于庞大,求解逆将会带来巨大的时间开销。这时会考虑使用梯度下降法来求解。
四、梯度下降法求解
梯度下降法的思想是:从某点开始,求出该点的梯度向量,给定学习率 。沿着梯度向量的反方向,以步长
,经过迭代,最终可能会收敛到函数最小值附近。
为了方便用图形说明,设成本函数: ,下图是整个迭代的过程。
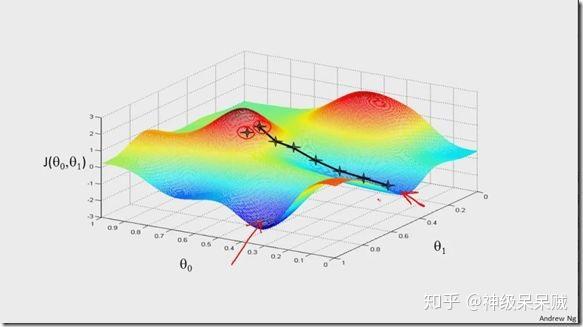
观察上图会发现,函数可能会陷入局部最优解。但对于凸函数来说,则一定会收敛到全局最优解。需要注意的是,当学习率取得过大,函数可能会难以收敛到最优解。反之,迭代收敛速度会变得缓慢。本例中所使用的均方误差函数,直观地说明图像就好比一个开口朝上地碗似的,因此必定会收敛到全局最有点
一般情况下,每次迭代过程中有:
迭代过程中,成本函数的值会逐渐减小,反应在该模型中就是 ,即预测值相对于真实值的差距会逐步缩小。最终可以在
个样本的集合中,拟合出较为合适的近似函数。
五、逻辑回归基本形式
上述过程可以得到连续区间的值,对于分类问题来说。需要将结果映射到一个离散的空间中,自然地想到,通过给定阈值可以很好地将结果归类。逻辑回归比较常用于这种问题。以二分类问题为例,其 ,通过sigmoid函数可以将输出结果是连续值映射到 概率值
上。
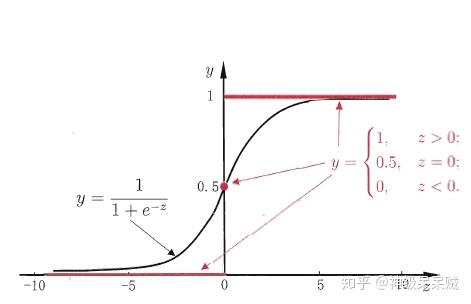
当z的值很大时,y的值趋近于1。当z值很小时,y值趋近于0
将之前的线性回归函数与sigmoid函数联立中:
如果使用均方误差代价函数,会出现,当sigmoid函数逐步趋近于0/1时,函数的梯度变得平缓,因此所求导数值会非常小,所以每次梯度下降的步长会很小,导致整个收敛过程变得非常缓慢。下面进行一个简单的推导来说明这种现象:
为了简单起见,以单个样本为例,考虑输入的特征属性仅为1,则有:
,
,
推导:
观察上述式子,当 很大或者很小时,
值也会保持一个很小的值,因此会导致收敛速度缓慢。
六、逻辑回归中的交叉熵函数
对于二分类问题,交叉熵函数(此处的log以e为底)可以很好的避免上述的问题:
接着开始推导交叉熵函数。由于整个样本的分布满足参数为 的伯努利分布,在样本空间
上:
因此样本 的分布律是:
由似然函数:
为了构建近似样本真实的概率分布,需要取似然函数的最大值,因此对似然函数两边取对数并乘以-1,即最小化下面的式子:
通过最小化代价函数,可以得到一个近似于训练样本的概率分布。
七、多分类问题
对于多分类问题,可以训练多个二分类模型来。最简单的例子就是对A,B,C三种类别进行分类。分别训练用于分别A、B和C的模型,B、A和C的模型,C、A和B的模型。
参考文献:
1.周志华. 机器学习[M]. 清华大学出版社, 2016.
2.Ian Goodfellow,Yoshua Bengio,Aaron Courville.深度学习[M].人民邮电出版社,2017
3.Andrew Ng 机器学习系列课程