线性回归

引入

下表中数据包含工资与年龄两个特征，现欲根据这两个特征预测银行贷款金额。即通过工资与年龄预测贷款额度

工资	年龄	额度
4000	25	20000
8000	30	70000
5000	28	35000
7500	33	50000
12000	40	85000

模型

我们可将工资、年龄设为x1,x2，将要求解的结果设为y.而要我们要在这么多点中找一个到各点之间距离最小的一个平面（高维类似）

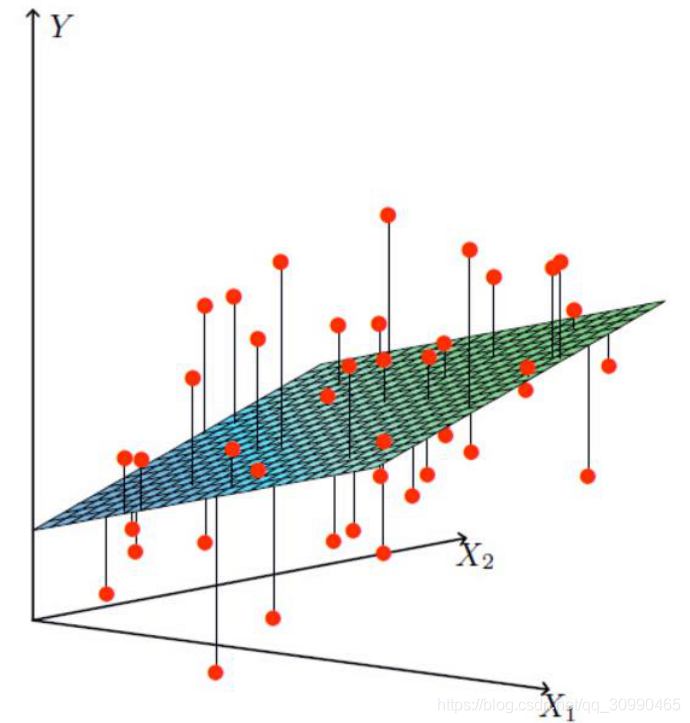
转换为数学模型

设 $\theta_{1}$ 、 $\theta_{2}$ 分别为年龄与工资对应的参数或者说比重,而 $\theta_{0}$ 为偏置
得到如下公式

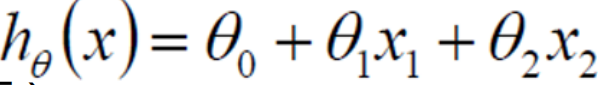
将公式进行整理得到：
$h_\theta(x)=\sum_{i=0}^{n}\theta_ix_i=\theta^Tx$

误差

通过公式计算得到的结果为预测值，与真实值或多或少总有些差异（我们使用 $\epsilon$ 表示误差）
对于每个样本都有
$y^{(i)}=\theta^Tx^{(i)}+\epsilon^{(i)}$
$\epsilon^{(i)}$ 遵循均值为0方差为 $\sigma^2$ 的正态分布(高斯分布)，正态分布样例如下图

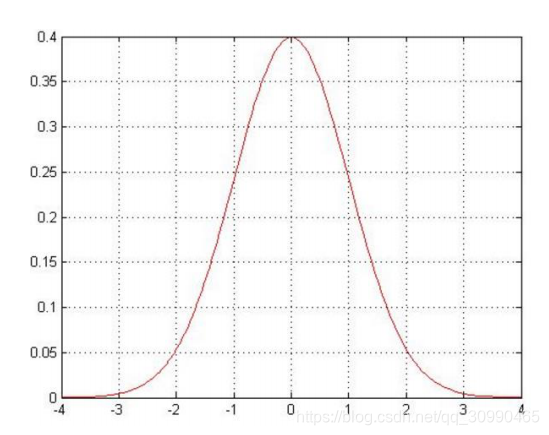
我们可列如下式子：
（1） $y^{(i)}-\theta^Tx^{(i)}=\epsilon^{(i)}$
（2） $p(\epsilon^{(i)})={1\over\sqrt{2\pi}\sigma}exp(-{-(\epsilon^{(i)})^2\over2\sigma^2})$
将（1）式中计算得到的 $\epsilon^{(i)}$ 代入（2）中得到
$p(y^{(i)}|x^(i);\theta)={1\over\sqrt{2\pi}\sigma}exp(-{{y^{(i)}-\theta^Tx^{(i)}}^2\over2\sigma^2})$ （3）

通过误差求解参数

使用似然函数进行误差求解
似然函数在百度百科上的定义:
似然函数是一种关于统计模型参数的函数。给定输出x时，关于参数θ的似然函数L(θ|x)（在数值上）等于给定参数θ后变量X的概率：L(θ|x)=P(X=x|θ)
在这里我的理解为（3）式得到的是一个概率值，即误差的概率值，误差自然是越小越好，当正态分布均值为0时，误差越接近于0概率越大，似然函数是多个概率值的累乘，即多个误差值出现概率的相乘，所以要使似然函数的值尽可能大。可得如下公式：
$L(\theta)=\prod^m_{i=1}p(y^{(i)}|x^(i);\theta)=\prod^m_{i=1}{1\over\sqrt{2\pi}\sigma}exp(-{{y^{(i)}-\theta^Tx^{(i)}}^2\over2\sigma^2})$
由于累乘比较难计算，则使用ln的方式将累乘的计算转换成累加
$logL(\theta)=\prod^m_{i=1}p(y^{(i)}|x^(i);\theta)=log\prod^m_{i=1}{1\over\sqrt{2\pi}\sigma}exp(-{{y^{(i)}-\theta^Tx^{(i)}}^2\over2\sigma^2})$
展开化简得到如下结果：（偷懒下面的都用截图了）
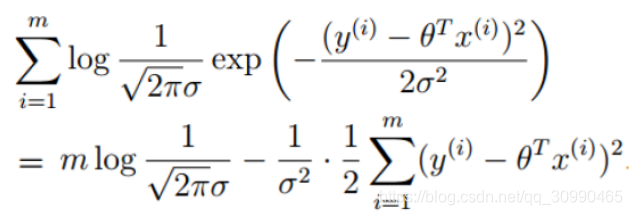
在这里插入图片描述
观察式子可以发现，-左边的式子是定值，想要使概率达到最大，则右边的值应该越小越好，从而可以得到

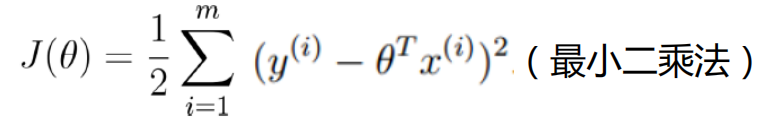
现在问题转换为求误差平方和的最小值，即J( $\theta$ )得到最小值。
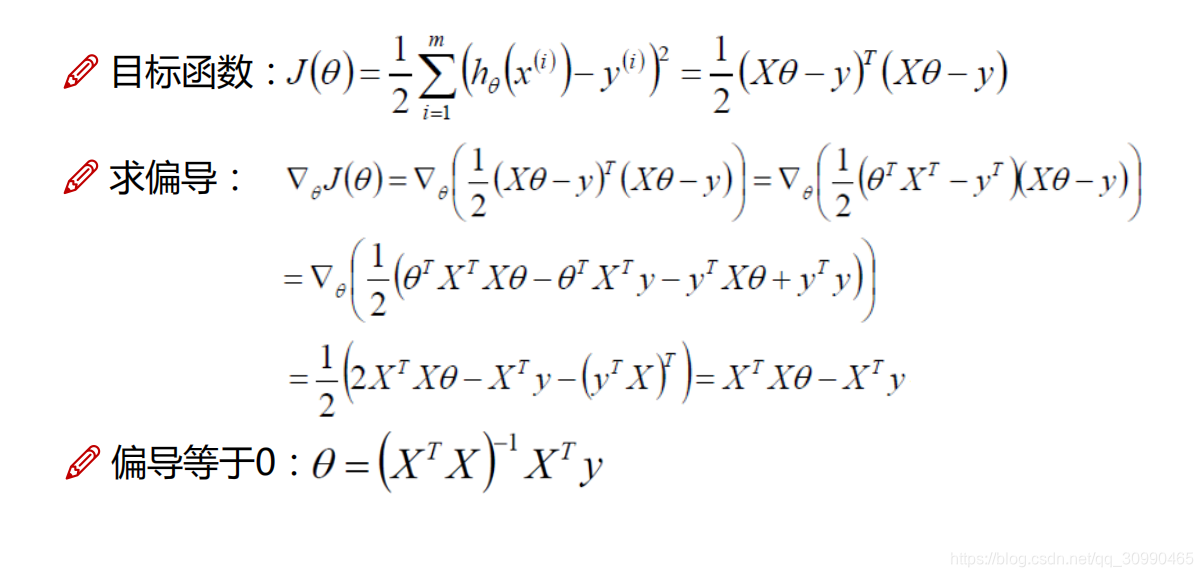
在这里插入图片描述
当求得偏导等于0时我们取得极小值，此时经过化简可以求出 $\theta$ 的值，当然结果是矩阵形式

评估

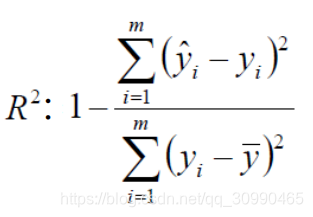
在这里插入图片描述
通常我们使用 $R^2$ 作为评估标准，上图的 $\sum^m_{i=1}(\hat{y}_i-y_i)^2$ 称为残差平方和，即预测值和真实值的差值，他们越小越好，即-号右式越小越好，则 $R^2$ 越接近与1则拟合度越高

另一种求解参数方式–梯度下降

并非所有的目标函数都可以像像线性回归一样通过似然函数求解 $\theta$ ,此时就要使用到梯度下降的方法
例如当我们经过计算整理得到一个损失函数（通常是预测值和目标值差值的平方），那么我们需要顺着损失减少的方向一步一步的进行 $\theta$ 的更新
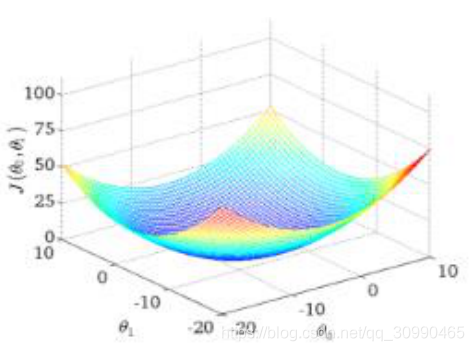
在这里插入图片描述
损失函数如上图（以两个 $\theta$ 值为例），当损失值达到最低点时，就可以得到最佳的结果。我们需要一步一步进行更新
在更新损失函数中的 $\theta$ 值时，（1）需要考虑每一步的步长，如果步长太大则容易“走偏”，步长太小则需要大量时间去走到最佳点，通常把步长称之为学习率（2）需要考虑每一步的方向，选择合适的方向才能达到最低点。通常会使用求偏导的方式求解合适的方向

梯度下降的几种方式

设目标函数为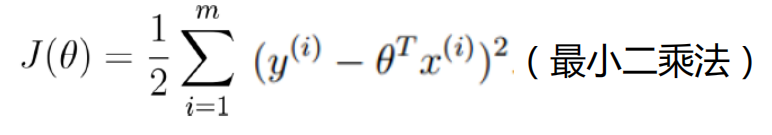在这里插入图片描述
(1)批量梯度下降：
将所有的样本都考虑在内，也就是每一个样本都参与每一次梯度下降的计算，容易得到最优解，但缺点是运算速度慢
（2）随机梯度下降

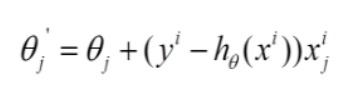
每次随机取得一个样本进行计算，优点是迭代速度非常快，但缺点是并非每次都朝着最优的方向迭代
（3）小批量梯度下降
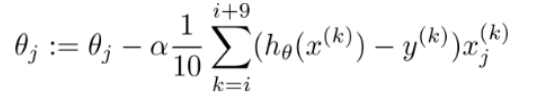
在这里插入图片描述
每次取得一小批数据进行计算，计算消耗比较小，更实用
###梯度下降学习率的影响
梯度决定了方向，学习率决定了一次走多远，通常不可以走太远。下图为不同学习率得到更新损失函数的效率

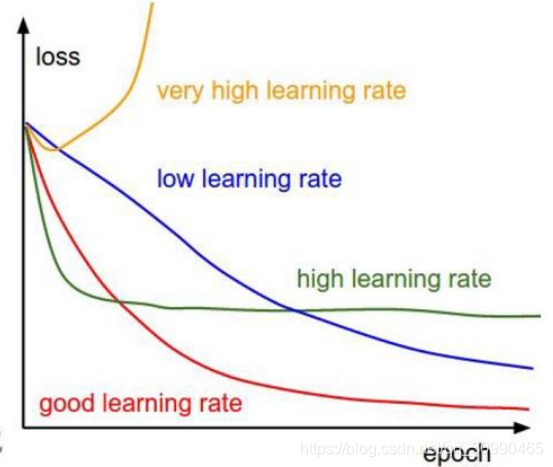
在图中可以看到一个合适的学习率可以按照较快的速率更新到理想的情况（损失最低的情况），当学习率太低时，损失函数则会更新的很慢，当学习率过高时有可能在更新到某一程度下停止更新（梯度变为0），甚至往相反方向更新

线性回归注意事项（引用）

（1）对异常值敏感，应剔除。
（2）只适合处理线性关系，若自变量和因变量间有比较强的非线性关系，应该对自变量进行一定的转换，比如取对数、开方、取平方根等。
（3）多元线性回归应用有一定的前提假设，自变量是确定的变量，而不是随机变量，自变量间没有线性相关，随机误差呈正态分布，随机误差项具有均值为0以及等方差性。

逻辑回归

逻辑回归是一种广义上的线性回归，也可以是y=ax+b这样的形式，但经过函数转换后转换为只有0~1的一个值，通常在做二分类时经常使用它。

Sigmod函数

通常逻辑回归在处理二分类问题时使用，通过计算两种情况的概率从而做出预测，因此就需要将之转换为0~1概率问题。此时就会用到sigmod函数
公式: $g(z)={1 \over {1+e^{-z}}}$ 其中自变量z可取任意实数，而g(z)得到的结果在0到1之间,入下图
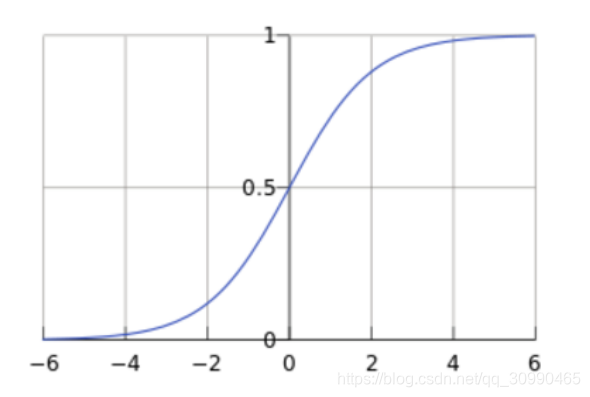
在这里插入图片描述
如图可以看到，当g(z)高于0.5时我们可以认为它可以被分类为1，低于0.5时可以被分类为0

举例

将线性回归的例子代入到sigmod中，预测函数变为
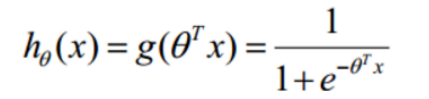
在这里插入图片描述
其中

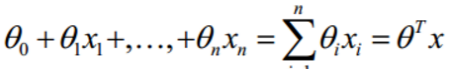
紧接着我们可以得到:

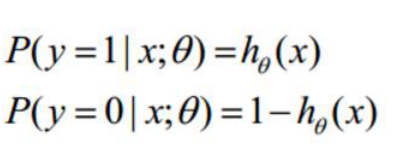
分别对应分类为1的概率与分类为0的概率，经过整合后：

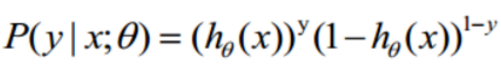
当y取值为1时，右端1-y为0,则 $(1-h_\theta(x)^{1-y})$ 结果为1，可得y为1的概率，同理当y取0时左端y为0可得y为0的概率

求解出最合适的参数

这里我们也使用似然函数，即经过一系列计算后我们想要让概率最大。如当y的值为0时我想让y=0情况下的计算结果达到概率尽可能接近1
似然函数：
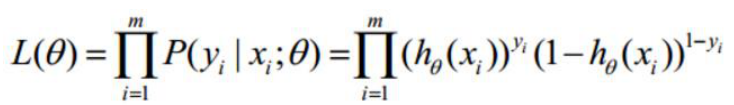
在这里插入图片描述
求解对数：

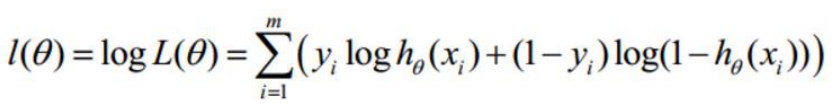
此时不再像求解损失函数一样要取得最小值，而是求解最大值，将式子经过转换变为求解梯度下降问题：
如下式：

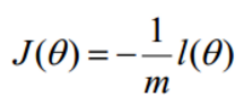
紧接着我们求解梯度方向（求偏导）：

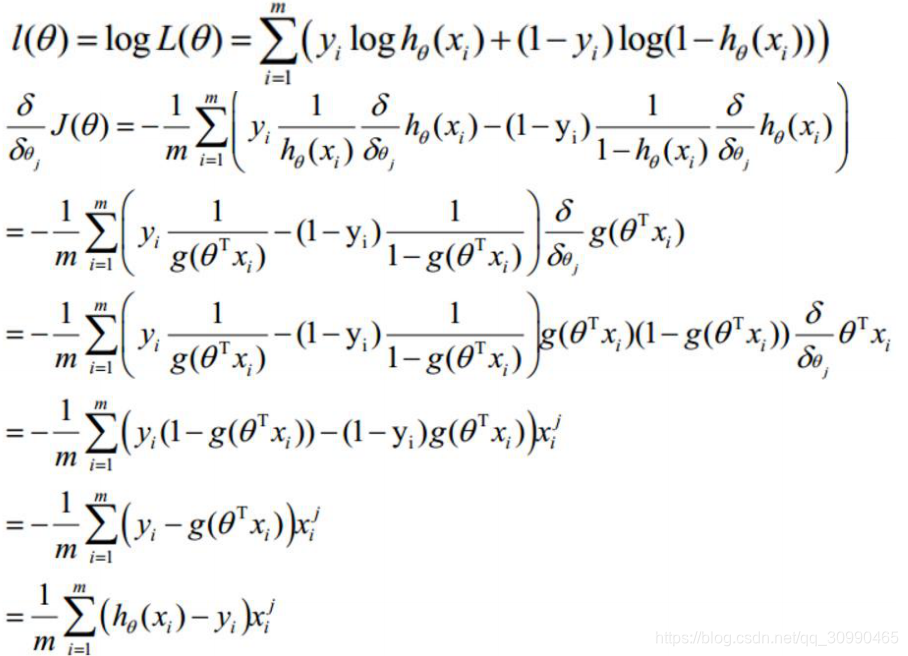
其中 $x^j_i$ 中i代表第i个样本,j代表需要更新的第j个参数
最终得到参数更新的式子：
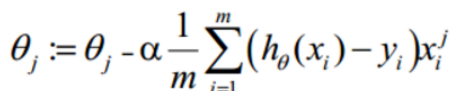
在这里插入图片描述
其中 $\alpha$ 为学习率