机器学习与高维信息检索 - Note 3 - 逻辑回归（Logistic Regression）及相关实例

3. 逻辑回归

在谈论逻辑回归时，一般的设定是，我们有数据点$X\in {\mathbb{R}}^p$和输出变量 Y ∈ { − 1 , + 1 } Y\in\{-1,+1\} Y∈{ −1,+1}。这是一个所谓的二元分类问题。

其任务是在预定的函数类别$\mathcal{F}$中找到函数$f$，使$\mathrm{sign}f(X)$能够尽可能好地预测$Y$。一个常用的损失函数用来衡量预测函数的 “准确性”，其动机是错误分类的数量，即如果$f(X)$的符号与真实输出$Y$的符号不一致。我们使用0.1损失函数

$$L_{0,1}(Y,f(X))=\{\begin{array}{ll}1& \text{ if }Y\mathrm{sign}f(X)\le 0\\ 0& \text{ otherwise }\end{array}\text{\hspace{1em}(3. 1)}$$

来完成这项工作。

为了在给定的训练样本集${\left(x_i,y_i\right)}_{i=1,\dots ,n}$中找到最佳预测函数$f\in \mathcal{F}$，目标是找到最小化经验预期损失的$f\in \mathcal{F}$。

$$\frac{1}{n}\sum _{i=1}^n{L}_{0,1}\left(y_i,f\left(x_i\right)\right)\text{\hspace{1em}(3.2)}$$

然而，要找到这个问题的最小值在数值上是不可行的。即使只是考虑到一类仿射函数${\mathcal{F}}_{\text{aff }}$，这也很难用数值来解决，因为损失函数既不连续也不可分。为了使其更容易解决，我们用一个凸损失函数(convex loss function) 来近似（非连续、非凸的）函数$L_{0,1}$。

补充: 凸性 Convexity

定义3.1

令$\mathcal{C}\subset {\mathbb{R}}^n$是一个凸集，即对于任何一对元素$x_1,x_2\in \mathcal{C}$来说 ，点$t{\mathbf{x}}_2+(1-t){\mathbf{x}}_1$ 也是$\mathcal{C}$的一个元素，对于所有$t\in [0,1]$。如果对于所有${\mathbf{x}}_1,{\mathbf{x}}_2\in \mathcal{C},t\in [0,1]$，有$tf\left({\mathbf{x}}_2\right)+(1-t)f\left({\mathbf{x}}_1\right)\ge f\left(t{\mathbf{x}}_2+(1-t){\mathbf{x}}_1\right)$，一个函数$f:\mathcal{C}\to \mathbb{R}$被称为凸的。如果不等式是严格的，它就被称为严格凸的。

例: $f:{\mathbb{R}}^{+}\to \mathbb{R},x\mapsto 1/x$是凸的。

定理3.2

如果$f，g$是凸的，那么

• $h=\max (f,g)$
• $h=f+g$
• $h=g\circ f$ if $g$ is non-decreasing

图3.1：$L_{0,1}$和对数损失，横轴为$t:=yf(x)$。

定理3.3

严格凸函数的局部最小值与它的全局最小值相吻合。如果它存在的话，它是唯一的。

对于目前的问题，这意味着如果我们选择$f$是仿射的（即$f(\mathbf{x})=$ ${\mathbf{w}}^{\top }\mathbf{x}+b$，根据定义是凸的），作为损失函数，我们使用凸的对数损失函数$\ell (t)=log\left(1+e^{-t}\right)$。两者的结合是凸的。为了看到这一点，计算二阶导数并研究其黑森矩阵。结果发现，它只有非负的特征值。选择对数损失的原因是，它可以被解释为$L_{0,1}$损失的凸近似值，如图3.1所示。给定一些训练数据 { ( x i , y i ) } i = 1 , … , N \left\{\left(\mathbf{x}_{i}, y_{i}\right)\right\}_{i=1, \ldots, N} { (xi​,yi​)}i=1,…,N​，我们可以通过解决优化问题找到最佳参数$w$和$b$。

$$\underset{\mathbf{w}\in {\mathbb{R}}^p,b\in \mathbb{R}}{\min }\frac{1}{n}\sum _{i=1}^n\log \left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)\right).\text{\hspace{1em}(3. 3)}$$

成本函数的凸性

为简单起见，我们只考虑线性$f$的成本函数。对仿射$f$的扩展是直截了当的。让我们用以下方式表示它
$$F(\mathbf{w})=\sum _{i=1}^n\log \left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)\right).$$

我们还使用辅助函数$g(z)=1/\left(1+e^{-z}\right)$，其中$g^{\prime }(z)=g(z)(1-g(z))$。那么，$F$的一次和二次偏导是
$$\frac{\partial }{\partial w^{(j)}}F(\mathbf{w})=-\sum _i{y}_i{x}_i^{(j)}\left(1-g\left(y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)$$

与

$$\frac{\partial }{\partial w^{(j)}\partial w^{(k)}}F(\mathbf{w})=\sum _i{y}_i^2{x}_i^{(j)}{x}_i^{(k)}g\left(y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\left(1-g\left(y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right),$$

其中$y_i^2=1$。为了证明该函数为非负定值，我们需要证明对所有$a$而言$a^{\top }{\nabla }^{2}Fa\ge 0$。我们定义辅助变量$P_i=g\left(y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\left(1-g\left(y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)$和${\rho }_i^{(j)}=x_i^{(j)}\sqrt{P_i}$。那么有

$$a^{\top }{\nabla }^{2}Fa=\sum _i\sum _{j,k}{a}_i{a}_j{x}_i^{(j)}{x}_i^{(k)}{P}_i=\sum _i{a}^{\top }{\rho }_i{\rho }_i^{\top }a\ge 0.$$

这对任何凸函数和仿射函数的联合都是成立的。

在下文中，我们将对这个优化问题进行概率性解释。首先，请注意，鉴于观察到的$Y=y$的条件概率$\mathrm{x}$被定义为

$$\mathrm{Pr}(Y=y\mid x)=\exp (-\ell (y,f(x)))=\frac{1}{1+\exp \left(-y\left({\mathbf{w}}^{\top }\mathbf{x}+b\right)\right)}.\text{\hspace{1em}(3. 4)}$$

为了找到（3.3）的解决方案，通常的做法是使用基于梯度的方法。最简单的形式是梯度下降法，在一个给定的迭代点，我们计算梯度，然后在该梯度的负方向迈出一步。函数 $F(\mathbf{w},b)={\sum }_i\log \left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)\right)$可以通过计算偏导来确定

$$\begin{array}{rl}\frac{\partial }{\partial w^{(k)}}F(\mathbf{w},b)& =\sum _{i=1}^n\frac{\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}{1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}\left(-y_i{x}_i^{(k)}\right)\\ & =\sum _{i=1}^n\frac{1}{1+\exp \left(y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}\left(-y_i{x}_i^{(k)}\right)\\ & =\sum _{i\mid y_i=1}\frac{1}{1+\exp \left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)}\left(-x_i^{(k)}\right)+\sum _{i\mid y_i=-1}\frac{1}{1+\exp \left(-{\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)}\left(x_i^{(k)}\right)\end{array}$$

系数$1/\left(1+\exp \left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)$和 $1/\left(1+\exp \left(-{\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)$是错误的预测概率。(参照（3.4））

因此，当我们朝着负梯度的方向迈出一步时，我们就会朝着这些错误的 "反方向 "前进。这就是为什么梯度下降方法也被称为错误驱动方法的原因。当前模型的错误（这里由一些权重$(\mathbf{w},b)）$被用来改进它。梯度指向的方向是使当前模型中的错误最小化。

总的来说：

逻辑回归是一种监督分类方法，决策函数是仿射的，损失用 $L(y,f(\mathbf{x}))=\log \left(1+e^{-yf(\mathbf{x})}\right))$衡量。最佳参数${\mathbf{w}}^{\star },b^{\star }$是通过最小化经验预期损失而找到的，即${\min }_{\mathbf{w},b}\frac{1}{N}\sum \log \left(1+e^{-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)}\right)$。一旦确定了最佳的${\mathbf{w}}^{\star },b^{\star }$，我们就可以通过计算$\mathrm{sign}\left({\mathbf{w}}^{\star \top }{\mathbf{x}}_{\text{new }}+b^{\star }\right)$对一个新数据点${\mathbf{w}}^{\star },b^{\star }$进行分类。我们还可以通过公式(3.4)计算出这种分类正确的概率。

3.1逻辑回归的替代方法

首先，请注意，逻辑回归这个名字可能会产生误导，因为事实上逻辑回归并不是一种回归方法，而是一种分类方法。上一节更多的是以优化为目的，而在这里，我们提供了一种更多的统计方法来处理逻辑回归。

例:
我们试图预测在某些参数下的死亡概率。让$x_1$为一个人的年龄，$x_2$为性别（0对应男性，1对应女性），$x_3$为胆固醇水平。我们假设可以将这些数值以线性方式组合起来，从而得到一个与死亡概率有某种关联的实际数值

$$w_0+w_1{x}_1+w_2{x}_2+w_3{x}_3={\mathbf{w}}^{\top }\mathbf{x}$$

有$\mathbf{x}={\left[1,x_1,x_2,x_3\right]}^{\top },\mathbf{w}={\left[w_0,w_1,w_2,w_3\right]}^{\top }$。$w_i$的值称为权重，$w_0$称为偏置。得到的值在$\mathbb{R}$中。为了将其塑造成一个概率，我们需要一个函数$\sigma$，将这个值压缩到$[0,1]$的区间内。一个能实现这一目的的函数是逻辑回归函数

$$\sigma (a)=\frac{1}{1+e^{-a}}\text{\hspace{1em}(3.5)}$$

得到的模型是$P(\text{死亡}\mid x)=\sigma \left({\mathbf{w}}^{\top }\mathbf{x}\right)$。

---

更一般地说，我们考虑二元分类问题的训练数据 D = { ( x 1 , z 1 ) , … , ( x n , z n ) } , x i ∈ R d , z i ∈ { 0 , 1 } D=\left\{\left(\mathbf{x}_{1}, z_{1}\right), \ldots,\left(\mathbf{x}_{n}, z_{n}\right)\right\}, \mathbf{x}_{i} \in \mathbb{R}^{d}, z_{i} \in\{0,1\} D={ (x1​,z1​),…,(xn​,zn​)},xi​∈Rd,zi​∈{ 0,1} ，输入和输出变量的依赖性模型为$z_i\propto \mathrm{Bernoulli}\left(\sigma \left({\mathbf{w}}^{\top }\mathbf{x}\right)\right)$，其中我们假定$z_i$是独立的。

为了训练这个模型，我们要找到给定$D$的$w$的最大似然估计，即

$${\mathbf{w}}_{\mathrm{M}\mathrm{L}\mathrm{E}}=\arg \underset{\mathbf{w}}{\max }\mathrm{Pr}(D\mid \mathbf{w})$$

有

$$\mathrm{Pr}(D\mid \mathbf{w})=\prod _{i=1}^n\mathrm{Pr}\left(z_i\mid {\mathbf{x}}_i,\mathbf{w}\right)=\prod _{i=1}^n\sigma {\left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)}^{z_i}{\left(1-\sigma \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)}^{1-z_i}\text{\hspace{1em}(3.6)}$$

出于优化目的，通常使用上述条件概率的负$\log$，即
$$L(\mathbf{w})=-\log \mathrm{Pr}(D\mid w)=-\sum _{i=1}^n{z}_i\log \left(\sigma \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)+\left(1-z_i\right)\log \left(1-\sigma \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)\text{. }\text{\hspace{1em}(3.7)}$$

各自的梯度（相对于$w$）由以下公式给出

$$\mathbf{g}={\nabla }_{\mathbf{w}}L(\mathbf{w})=\sum _{i=1}^n\left(\sigma \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)-z_i\right){\mathbf{x}}_i=\mathbf{X}\left(\sigma \left({\mathbf{X}}^{\top }\mathbf{w}\right)-\mathbf{z}\right)\text{\hspace{1em}(3.8)}$$

与$\mathbf{X}=\left[{\mathbf{x}}_1,\dots ,{\mathbf{x}}_n\right]\in {\mathbb{R}}^{d\times n}$。相应的$w$的黑塞矩阵$\mathbf{H}$给出为

$$\mathbf{H}={\nabla }_{\mathbf{w}}^{2}L(\mathbf{w})={\mathbf{X}\mathbf{B}\mathbf{X}}^{\top }\text{\hspace{1em}(3.9)}$$

有$\mathbf{B}=\mathrm{diag}\left(\sigma \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\left(1-\sigma \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)\right)\in {\mathbb{R}}^{n\times n}$ 。黑塞矩阵$\mathbf{H}$是半正定的，因此$L$是凸的。

假设Hessian是可逆的。那么牛顿方法的迭代形式为

$$\begin{array}{rl}{\mathbf{w}}_{t+1}& ={\mathbf{w}}_t-{\mathbf{H}}^{-1}\mathbf{g}\\ & ={\mathbf{w}}_t-{\left({\mathbf{X}\mathbf{B}\mathbf{X}}^{\top }\right)}^{-1}\mathbf{X}\left(\sigma \left({\mathbf{X}}^{\top }\mathbf{w}\right)-\mathbf{Z}\right)\\ & ={\left({\mathbf{X}\mathbf{B}\mathbf{X}}^{\top }\right)}^{-1}{\mathbf{X}\mathbf{B}\mathbf{r}}_t\end{array}\text{\hspace{1em}(3.10)}$$

有${\mathbf{r}}_t={\mathbf{X}}^{\top }{\mathbf{w}}_t-{\mathbf{B}}^{-1}\left(\sigma \left({\mathbf{X}}^{\top }{\mathbf{w}}_t\right)-\mathbf{z}\right)$. 这就是加权最小二乘法问题的解决方案 $\arg {\min }_{\mathbf{w}}.{\sum }_i{b}_i{\left(r_i-{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)}^2$.

练习：证明方程(3.7)与方程(3.3)在标量因子$1/n$以内是等价的。

---

proof

首先，注意$\log \left(\sigma \left({\mathbf{w}}^{\top }\mathbf{x}\right)\right)=-\log \left(1+\exp \left(-{\mathbf{w}}^{\top }\mathbf{x}\right)\right)$ 和$\log \left(1-\sigma \left({\mathbf{w}}^{\top }\mathbf{x}\right)\right)=-\log \left(1+\exp \left({\mathbf{w}}^{\top }\mathbf{x}\right)\right)$。因此，公式（3.7）等价于

$$L(\mathbf{w})=\sum _{i=1}^n{z}_i\log \left(1+\exp \left(-{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)+\left(1-z_i\right)\log \left(1+\exp \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)\text{\hspace{1em}(3.11)}$$

由于$z_i$不是0就是1，我们可以将和改写为

$$L(\mathbf{w})=\sum _{z_i=1}\log \left(1+\exp \left(-{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)+\sum _{z_i=0}\log \left(1+\exp \left({\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right).\text{\hspace{1em}(3.12)}$$

现在，将标签$z_i$与（3.3）中的标签$y_i$相比较，我们看到$z_i=1\iff y_i=1$，$z_i=0\iff y_i=-1$，所以

$$\begin{array}{rl}L(\mathbf{w})& =\sum _{y_i=1}\log \left(1+\exp \left(-y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)+\sum _{y_i=-1}\log \left(1+\exp \left(-y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right)\\ & =\sum _{i=1}^n\log \left(1+\exp \left(-y_i{\mathbf{w}}^{\top }{\mathbf{x}}_i\right)\right),\end{array}\text{\hspace{1em}(3.13)}$$

与方程(3.3)相吻合，其系数为$1/n$。

3.2 线性可分性和逻辑回归

需要注意的是，逻辑回归在线性可分离的训练集上可以过度拟合。当两个类1和$-1$是线性可分离的，我们可以找到一个超平面$\left({\mathbf{w}}_s,b_s\right)$，使得以下不等式成立。

$$y_i\left({\mathbf{w}}_s^{\top }{\mathbf{x}}_i+b_s\right)>0\forall i.\text{\hspace{1em}(3.14)}$$
考虑以下定理。

定理3.4

对于线性可分离的、非空的训练集，损失函数

$$F(\mathbf{w},b)=\sum _{i=1}^n\log \left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)\right)\text{\hspace{1em}(3.15)}$$

在${\mathbb{R}}^{p+1}$中没有全局最小值。

---

证明
首先让我们来描述$F$的全局最小值。它是$\left({\mathbf{w}}^{\ast },b^{\ast }\right)\in {\mathbb{R}}^{p+1}$ 中的一个点，即

$$F(\mathbf{w},b)\ge F\left({\mathbf{w}}^{\ast },b^{\ast }\right)\forall (\mathbf{w},b)\in {\mathbb{R}}^{p+1}\text{\hspace{1em}(3.16)}$$
存在。如果训练集是非空的，那么损失函数就是严格的正定的。因此，$F$的最小值是某个正数$\epsilon$，即

$$F\left({\mathbf{w}}^{\ast },b^{\ast }\right)=\epsilon >0.\text{\hspace{1em}(3.17)}$$

现在我们将通过矛盾法来证明全局最小值的缺失。假设有一个点$\left({\mathbf{w}}_s,b_s\right)$和一个实数$\epsilon >0$，使得以下条件成立。

$$y_i\left({\mathbf{w}}_s^{\top }{\mathbf{x}}_i+b_s\right)>0\forall i\text{ and }F(\mathbf{w},b)\ge \epsilon \forall (\mathbf{w},b)\in {\mathbb{R}}^{p+1}.\text{\hspace{1em}(3.18)}$$

对于每个$i$，定义以下标量值
$${\xi }_i=y_i\left({\mathbf{w}}_s^{\top }{\mathbf{x}}_i+b_s\right)\text{\hspace{1em}(3.19)}$$

考虑以下方程

$$f_i(h)=\log \left(1+\exp \left(-h{\xi }_i\right)\right)\text{\hspace{1em}(3.20)}$$

很容易看出，$x{i}_i$对于任何$i$都是严格的正数，因此$f_i(h)$随着$h$接近$\infty$而接近0。如果我们考虑$i$的总和，即

$$\underset{h\to \infty }{\lim }\sum _{i=1}^n{f}_i(h)=F\left(h{\mathbf{w}}_s,h{b}_s\right)=0.\text{\hspace{1em}(3.21)}$$

换句话说，对于任何$\epsilon >0$，我们可以找到一个实数$\eta >0$，这样，对于任何$h\ge \eta$，下面的不等式都成立。
$$F\left(h{\mathbf{w}}_s,h{b}_s\right)<\epsilon \text{\hspace{1em}(3.22)}$$

这直接与假设（3.18）相矛盾，因为我们可以选择$\mathrm{w}=h{\mathrm{w}}_s$和$b=h{b}_s$，且有$h\ge \eta$。

证明表明，一旦找到一个分离超平面，损失函数的值总是可以通过增加超平面参数的大小而进一步降低。请注意，这对任何分离类的超平面都是真实的。在实践中，一个优化算法可以选择一个具有 "坏 "位置和方向的超平面，并增加参数的大小，直到达到最大迭代次数。

为了防止这种情况，通常通过引入正则器来惩罚$(\mathbf{w},b)$的大小，例如通过固定一个实数常数$\lambda >0$并将原始成本函数调整为

$$\tilde{F}(\mathbf{w},b)=F(\mathbf{w},b)+\lambda \left(\Vert \mathbf{w}{\Vert }^2+b^2\right)\text{\hspace{1em}(3.23)}$$

3.3 逻辑回归的额外内容

任务1. 考虑为数据样本 y ∈ { − 1 , 1 } y\in\{-1,1\} y∈{ −1,1}分配一个标签的二元分类问题。通过逻辑回归的方式对数据样本 y ∈ { − 1 , 1 } y \in\{-1,1\} y∈{ −1,1}进行二元分类。给定一个训练集 { ( x 1 , y 1 ) , … , ( x N , y N ) } \left\{\left(\mathbf{x}_{1}, y_{1}\right), \ldots,\left(\mathbf{x}_{N}, y_{N}\right)\right\} { (x1​,y1​),…,(xN​,yN​)}的标记数据。回顾一下，损失函数是由

$$L(\mathbf{w},b)=\sum _{i=1}^N\log \left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)\right)$$

3.3.1 梯度 ${\nabla }_{\mathbf{w},b}L$

解决方法： 根据链式法则，我们有

$$\begin{array}{rl}{\nabla }_{b}L& =\sum _{i=1}^N\frac{{\nabla }_b\left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)\right)}{1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}\\ & =-\sum _{i=1}^N{y}_i\frac{\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}{1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}\\ & =-\sum _{i=1}^N\frac{y_i}{1+\exp \left(y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}\end{array}$$

据此，我们得到

$$\begin{array}{rl}{\nabla }_{\mathbf{w}}L& =\sum _{i=1}^N\frac{1}{1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}{\nabla }_{\mathbf{w}}\left(1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)\right)\\ & =-\sum _{i=1}^N{y}_i\frac{\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}{1+\exp \left(-y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}{\mathbf{x}}_i\\ & =-\sum _{i=1}^N\frac{y_i}{1+\exp \left(y_i\left({\mathbf{w}}^{\top }{\mathbf{x}}_i+b\right)\right)}{\mathbf{x}}_i\end{array}$$

3.3.2 损失函数的全局最小值

假设训练集的两个类是线性可分离的，即有一个权重向量${\mathbf{w}}_s\in {\mathbb{R}}^p$，并且存在一个偏置$b_s$，从而
$$y_i\left({\mathbf{w}}_s^{\top }{\mathbf{x}}_i+b_s\right)>0\forall i$$
成立. 证明在此假设下，损失函数在$\left({\mathbf{w}}^{\ast },b^{\ast }\right)\in {\mathbb{R}}^{p+1}$中没有全局最小值。

解决方法:
$L$的全局最小值是指$\left(w^{\ast },b^{\ast }\right)\in {\mathbb{R}}^{p+1}$中的一对，这样
$$L(\mathbf{w},b)\ge L\left({\mathbf{w}}^{\ast },b^{\ast }\right)\forall (\mathbf{w},b)\in {\mathbb{R}}^{p+1}$$
成立。此外，对于非空的训练集，$L$是严格的正数，因此我们可以得出结论
$$L\left({\mathrm{w}}^{\ast },b^{\ast }\right)=\epsilon >0$$
假设有这样一个点存在。让我们定义
$$z_i=y_i\left({\mathbf{w}}_s^{\top }{\mathbf{x}}_i+b_s\right)$$
请注意，$z_i$对于每一个$i$都是严格的正数。考虑函数
$$f(h)=\sum _{i=1}^N\log \left(1+\exp \left(-h{z}_i\right)\right)$$
由于每个和都随着$h$接近$\infty$而接近0，$f(h)$也是如此，即
$$\underset{h\to \infty }{\lim }f(h)=0$$
观察平等的情况
$$f(h)=L\left(h{\mathbf{w}}_{\mathbf{s}},h{b}_s\right)$$
这意味着对于任何$\epsilon >0$，我们可以在$\mathbb{R}$中找到一个$h$，并设定$(\mathbf{w},b)=\left(h{\mathrm{w}}_{\mathrm{s}},h{b}_s\right)$ ，这样
$$L(\mathbf{w},b)<\epsilon$$
成立，这与$\left({\mathbf{w}}^{\ast },b^{\ast }\right)$的假设相矛盾，$L\left({\mathbf{w}}^{\ast },b^{\ast }\right)=\epsilon$是一个全局最小。

请注意，$\left({\mathbf{w}}_s,b_s\right)$所描述的超平面不一定是任何意义上的最优。根据算法的不同，这可能会导致 "非理想 "的超平面描述符的常数不断增加。

3.3.3 过拟合

为了避免3.3.2中的情况，可以通过增加一个平方范数控制器来惩罚$(w，b)$的范数。考虑修改后的损失函数
$$\tilde{L}(\mathbf{w},b)=L(\mathbf{w},b)+\lambda \left(\Vert \mathbf{w}{\Vert }^2+b^2\right)$$
其中$\lambda >0$是一个实值常数。计算梯度${\nabla }_{\mathbf{w},b}\tilde{L}$ 。

解决方法：
由于导数的线性特性，我们有
$${\nabla }_b\tilde{L}={\nabla }_{b}L+2\lambda b$$
和
$${\nabla }_{\mathrm{w}}\tilde{L}={\nabla }_{\mathrm{w}}L+2{\lambda }_{\mathrm{w}}$$

3.4 逻辑回归实例

下面的练习是建立在提取的特征表示之上的，但我们要用手动实现逻辑回归，即通过最小化讲义中第三章的$F(\mathbf{w})$来代替预先建立的分类器。为此，确保变量train、test、train_data_features和test_data_features（来自于提取的特征）被加载到你的IPython shell。

a) 编写一个PYTHON函数logistic_gradient，期望将训练集矩阵X_train、地面真实标签向量$y_{\text{train}}$和当前权重向量$w$作为其输入，并返回logistic回归的负对数似然函数的梯度$g$。关于数学定义，请参考讲义。

b) 编写一个PYTHON函数find_w，期望有一个训练集矩阵X_train，一个地面真实标签向量y_train，一个步长α和一个最大迭代数max_it，通过执行梯度下降确定最佳逻辑回归权重向量w_star，即在每个迭代中调用logistic_gradient。确保将仿射偏移量$w_0=b$纳入你的模型。

c) 手头的数据集相当大。应用标准梯度下降可能会导致Python抛出一个MemoryError异常。为了避免这种情况，我们将采用随机梯度下降法的一种变体，这种变体在训练深度神经网络方面已经被证明是成功的。在minibatch学习中，算法的每一次迭代都被一个所谓的epoch所取代。在每个历时中，训练集被随机划分为大小相等的子集，即迷你批。对于每个minibatch，梯度被计算出来，并只应用于minibatch中的样本。当每个minibatch的梯度步骤被执行时，一个epoch就结束了。修改find_w，使其能够进行小批量学习。你需要用$n_{-}$epochs替换max_it，并在函数定义中添加参数n_minibatch。注意：要注意梯度和损失函数的归一化。

d) 编写一个函数classify_log，有一个权重向量w和一个测试集矩阵X_test，通过逻辑回归对X_test中的样本进行分类，返回一个标签向量$y_{\text{test. }}$在train_data_features和test_data_features上测试find_w和classify_log的实现，10个epochs，minibatches大小为100，步长为alpha=1。

e) Logistic回归很容易出现过拟合。为了防止这种情况，可以使用正则器。调整实现方式，使其不是最小化$F(\mathbf{w})$，而是最小化项
$$F(\mathbf{w})+\lambda \Vert \mathbf{w}{\Vert }^2$$
其中$\lambda$是一个非负的正则化参数。用$\lambda =10^{-3}$测试实现方式。

3.4.1 使用python实现

相关python代码如下

import numpy as np
import pandas as pd
from bs4 import BeautifulSoup
import re
import nltk
import matplotlib.pyplot as plt

nltk.download('stopwords')  # Download text data sets, including stop words
from nltk.corpus import stopwords  # Import the stop word list
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.linear_model import LogisticRegression as LR
from sklearn.metrics import roc_auc_score as AUC


# function for preprocessing the data
def review_prepro(data, remove_stopwords=False):
    stops = stopwords.words('english')
    # remove HTML tags
    review_text = BeautifulSoup(data, 'lxml').get_text()
    # remove non-letters and numbers
    letters_only = re.sub('[^a-zA-Z]',
                          ' ',
                          review_text)
    # make all characters lower case and split the documents into single words
    words = letters_only.lower().split()

    if remove_stopwords:
        # remove stop words
        meaningful_words = [w for w in words if not w in stops]
        # return concatenated single string
        return ' '.join(meaningful_words)
    else:
        # or don't and concatenate to single string
        return ' '.join(words)


def classify_log(w, X_test):
    w0 = w[0]
    y_test = sigmoid(w0 + np.dot(X_test.T, w[1:]))
    return y_test


def train_data_prep(train, vectorizer):
    """
    preprocess the training data using the bag of words in Sklearn
    :param train:
    :return: processed training data
    """
    # load train data
    num_reviews = train['review'].size
    clean_train_reviews = []
    for i in range(num_reviews):
        if (i + 1) % 1000 == 0:
            print('\r Review {} of {} - Training'.format(i + 1, num_reviews), end="")
        clean_train_reviews.append(review_prepro(train['review'][i], remove_stopwords=True))

    # fit the vectorizer to the data
    train_data_features = vectorizer.fit_transform(clean_train_reviews)
    # convert to numpy array
    train_data_features = train_data_features.toarray()

    return train_data_features


def test_data_prep(test, vectorizer):
    """
    preprocess the testing data from the raw input
    :param test:
    :return: processed testing data
    """
    num_test_reviews = test['review'].size
    clean_test_reviews = []
    for i in range(num_test_reviews):
        if (i + 1) % 1000 == 0:
            print('\r Review {} of {}'.format(i + 1, num_test_reviews), end='')
        clean_test_reviews.append(review_prepro(test['review'][i], remove_stopwords=True))

    test_data_features = (vectorizer.transform(clean_test_reviews)).toarray()
    return test_data_features


def sigmoid(x):
    # https://timvieira.github.io/blog/post/2014/02/11/exp-normalize-trick/
    z = np.exp(-np.abs(x))
    return np.where(x >= 0.0, 1.0 / (1.0 + z), z / (1.0 + z))


def logistic_gradient(x_train, y_train, w, reg=0.0):
    g = -np.dot(x_train * y_train, sigmoid(-np.dot(w, x_train) * y_train)) / x_train.shape[1] + reg * np.sum(w ** 2)
    return g


def find_w(x_train, y_train, alpha, n_epochs, n_minibatch, reg=0.0):
    """
    Using this function to find the best w.
    :param x_train: the training data, which has the shapes [samples, features]
    :param y_train: the training label, which has the shapes [outputs,]
    :param alpha: step constant
    :param n_epochs: training epochs
    :param n_minibatch: we divided the training data into some small training set to accelerate the training speed.
    :param reg: the factor of the regularizer
    :return: the best weight w_star
    """
    x_train = x_train.T
    x_pre = np.ones((x_train.shape[0] + 1, x_train.shape[1]))
    x_pre[1:, :] = x_train
    w = np.ones((x_pre.shape[0],))
    print('x_pre shape ={}, w shape = {}'.format(x_pre.shape, w.shape))
    loss_ = []
    for k in range(n_epochs):
        loss = np.sum(-np.log(sigmoid(y_train * np.dot(w, x_pre)))) / x_pre.shape[1] + reg * np.sum(w ** 2)
        loss_.append(loss)
        rp = np.random.permutation(x_pre.shape[1])
        print('In {} iteration, the loss = {}'.format(k, loss))
        for it in range(x_pre.shape[1] // n_minibatch):
            delta_w = logistic_gradient(x_pre[:, rp[it * n_minibatch: (it + 1) * n_minibatch]],
                                        y_train[rp[it * n_minibatch:(it + 1) * n_minibatch]], w)
            w = w - alpha * delta_w
    return w,loss_


if __name__ == "__main__":
    # load the data
    train = pd.read_csv('labeledTrainData.tsv', header=0, delimiter='\t', quoting=3)
    test = pd.read_csv('labeledTestData.tsv', header=0, delimiter="\t", quoting=3)

    # download the stopwords
    stops = set(stopwords.words('english'))
    vectorizer = CountVectorizer(analyzer='word',
                                 tokenizer=None,
                                 preprocessor=None,
                                 stop_words=stops,
                                 max_features=5000)

    # process the data
    train_data_features = train_data_prep(train, vectorizer)
    test_data_features = test_data_prep(test, vectorizer)
    y_train = (np.array(train['sentiment'].values) - 0.5) * 2

    # (1) Testing implementation without regularizers
    W, W_loss = find_w(train_data_features, y_train, 0.8, 20, 100)
    y_pred = classify_log(W, test_data_features.T)
    y_test = test['sentiment'].values
    auc = AUC(y_test, y_pred)
    print('AUC score after 20 epochs:', auc)

    # (2) Testing implementation with regularizers to overdue mitigate the overfitting
    w, w_loss = find_w(train_data_features, y_train, 1, 20, 100, 1e-3)
    y_pred = classify_log(w, test_data_features.T)
    auc = AUC(y_test, y_pred)
    print('AUC score after 20 epochs:', auc)

    # plot
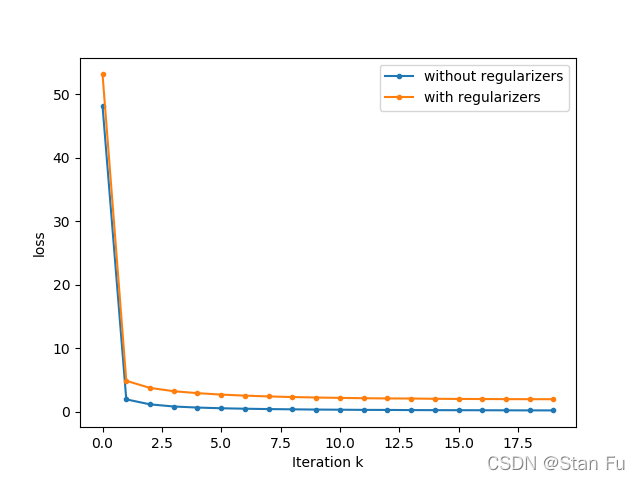
    fig = plt.figure()
    ax = fig.add_subplot(1, 1, 1)
    ax.set_xlabel('Iteration k')
    ax.set_ylabel('loss')
    ax.plot(W_loss, marker='.', label='without regularizers')
    ax.plot(w_loss, marker='.', label='with regularizers')
    ax.legend()
    plt.show()

输出为，

x_pre shape =(5001, 20000), w shape = (5001,)
In 0 iteration, the loss = 48.15060140614601
In 1 iteration, the loss = 1.9271375244901945
In 2 iteration, the loss = 1.1439895026827396
In 3 iteration, the loss = 0.8040511998178164
In 4 iteration, the loss = 0.637276530141581
In 5 iteration, the loss = 0.5275615696559821
In 6 iteration, the loss = 0.4531238182560532
In 7 iteration, the loss = 0.39835683526227206
In 8 iteration, the loss = 0.3585725270966355
In 9 iteration, the loss = 0.3208458216978429
In 10 iteration, the loss = 0.2989468342660105
In 11 iteration, the loss = 0.27127014988315357
In 12 iteration, the loss = 0.26380395477375235
In 13 iteration, the loss = 0.23870379629686295
In 14 iteration, the loss = 0.22874535039441457
In 15 iteration, the loss = 0.22097269464251518
In 16 iteration, the loss = 0.21411424494393824
In 17 iteration, the loss = 0.20234804193010983
In 18 iteration, the loss = 0.19146457065053046
In 19 iteration, the loss = 0.18977771952092898
AUC score after 20 epochs: 0.9201902430149848

x_pre shape =(5001, 20000), w shape = (5001,)
In 0 iteration, the loss = 53.15160140614601
In 1 iteration, the loss = 4.850572401123086
In 2 iteration, the loss = 3.7359586329298007
In 3 iteration, the loss = 3.2139682944306305
In 4 iteration, the loss = 2.907177612020046
In 5 iteration, the loss = 2.681058512521938
In 6 iteration, the loss = 2.5166307885635284
In 7 iteration, the loss = 2.392833861337298
In 8 iteration, the loss = 2.294087922661967
In 9 iteration, the loss = 2.2217974363161987
In 10 iteration, the loss = 2.161302804041983
In 11 iteration, the loss = 2.113409966477404
In 12 iteration, the loss = 2.0736801266948683
In 13 iteration, the loss = 2.061541837823529
In 14 iteration, the loss = 2.016740023535874
In 15 iteration, the loss = 1.9973296285347977
In 16 iteration, the loss = 1.9823663669782907
In 17 iteration, the loss = 1.967645885882539
In 18 iteration, the loss = 1.9572636195387196
In 19 iteration, the loss = 1.9538835403945283
AUC score after 20 epochs: 0.921975893241498