上一章：机器篇——线性回归

下一章：机器篇——决策树(一)

细讲了线性回归的推导和代码，图文结合，本章再接再厉，来讲解逻辑回归。大佬来了，请多多指教。

逻辑回归的理解

一. 回归与分类

1. 关于回归，给人直观的理解就是拟合

2. 对于二类线性可分的数据集，使用线性感知器就可以很好的分类

3. 但如果二类线性不可分的数据，无法找到一条直线能够将两种类别很好地区分，即线性回归的分类对于线性不可分的数据无法有效分类。

4. 诚然，数据线性可分可以使用线性分类器；如果数据线性不可分，可以使用非线性分类器。这里，似乎没逻辑回归什么事情。但是，如果想知道对于一个二分类问题，其具体的一个样例：不仅想知道该分类属于某一类，而且还想知道该类属于某一类的概率有多大。

5. 线性回归和非线性回归的问题都不能给予解答，假设其分类函数如下：

$\LARGE y = W^TX$

6. 因为概率的范围在 [0, 1] 之间，这就需要一个更好的映射函数，能够将分类的结果很好的映射成 [0, 1] 之间的概率，并且这个函数能够具有很好的可微分性。在这种需求下，大佬找到了这个映射函数，即 Sigmoid 函数。其形式如下：

$\LARGE g(z) = \tfrac{1}{1 + e^{-z}}$

7. Sigmoid & Logistic Regression

(1). 在学习 Logistic Regression 的时候，会出现一个重要的问题：

为什么 LR (Logistic Regression) 会使用 Sigmoid 函数，而不是其他的函数？

(2). 其实，上述的问题本身就是不对的。因为是使用了 Logistic Function (Sigmoid) ，所以才有了 Logistic Regression 这个名字。即：正是因为 Sigmoid 才有了 LR，而不是 LR 选择了 Sigmoid 函数。

8. 由于 LR 是使用回归函数做分类，而假设的回归函数为： $\large y = WX$ ，由于 Sigmoid 函数为 $\large g(z) = \tfrac{1}{1 + e ^{-z}}$ 。所以， $\large g(z)$ 是关于 $\large y$ 的函数，即：

$\LARGE \left\{\begin{matrix} y = WX& & \\ g(z) = \tfrac{1}{1 + e^{-z}} & & \end{matrix}\right.\Rightarrow g(w, x) = \tfrac{1}{1 + e^{-WX}}$

二. Sigmoid 的性质与目标函数

1. Sigmoid 函数的导数： $\large g'(z) = g(z)(1 - g(z))$

推导过程：

$\LARGE g'(z) = \frac{\partial g(z)}{\partial z}$

$\LARGE = \tfrac{-1}{(1 + e^{-z})^2}e^{-z}(-1)$

$\LARGE = \tfrac{e^{-z}}{(1 + e^{-z})^2}$

$\LARGE = \tfrac{1}{1 + e^{-z}}(1 - \tfrac{1}{1 + e^{-z}})$

$\LARGE = g(z)(1 - g(z))$

2. Sigmoid 函数的概率

因为 Sigmoid 函数的概率值在 [0, 1] 之间，即：

$\large p_{i}(right) = \left\{\begin{matrix} g(w, x_{i}) & p(positive): y_{i} = 1 \\ 1 - g(w, x_{i}) & p(negative): y_{i} = 0 \end{matrix}\right.$

所以对于每一条数据预测正确的概率：

$\LARGE p_{i}(right) = [g(w, x_{i})]^{y_{i}}[1 - g(w, x_{i})]^{1 - y_{i}}$

3. 全部预测正确的概率

由于 Sigmoid 函数服从正太分布，而且：

全部预测正确的概率 = 每一条数据预测正确的概率相乘

$\LARGE p(allRight) = \prod_{i = 1}^{m}p_{i}(right)$

4. LR 的目标函数

记 $\large p(allRight)$ 为 $\large L(\theta)$ ， $\large w$ 与 $\large \theta$ 等价。

由 $\LARGE p(allRight) = \prod_{i = 1}^{m}[g(w, x_{i})]^{y_{i}}[1 - g(w, x_{i})]^{1 - y_{i}}$

$\LARGE \Rightarrow L(\theta) = \prod_{i = 1}^{m}[h_{\theta}(x_{i})]^{y_{i}}[1 - h_{\theta}(x_{i})]^{1 - y_{i}}$

(通常，习惯把目标函数写成 $\large h_{\theta}(x)$ ，在这里： $\large h_{\theta}(x) = g(w, x)$ )

现在想找一组 $\large \theta$ ，使得上面的概率函数有最大值。由于对数函数 $\large ln$ 是单调递增的，所以当 $\large lnL(\theta)$ 最大时， $\large L(\theta)$ 也为最大，则：

$\LARGE l(\theta) = lnL(\theta)$

$\LARGE = \sum_{i = 1}^{m}[y_{i}h_{\theta}(x_{i}) + (1 - y_{i})ln(1 - h_{\theta}(x_{i}))]$

使 $\large l(\theta)$ 最大的 $\large \theta$ 生产出来的 $\large g(w, x)$ 全预测正确的概率最大。

5. 损失函数

通常，某个函数的结果越小，生成的模型就越好。因此，定义 $\large - l(\theta)$ 为 LR 的损失函数，求它的最小值。

$\large J(\theta) = \sum_{i = 1}^{m}[-y_{i}lnh_{\theta}(x_{i}) - (1 - y_{i})ln(1 - h_{\theta}(x_{i}))]$

6. 对 LR 梯度下降求出最优的 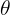$\large \theta$

$\large \theta = \theta - \alpha \frac{\partial J(\theta)}{\partial \theta}$

7. LR 梯度下降流程(与上一章讲的线性回归梯度下降相似)

(1). 随机产生一组初始值:

$\large \theta = (w_{0}, w_{1}, w_{2}, ......, w_{n})$

(2). 求梯度：

$\large g = \frac{\partial J(\theta)}{\partial \theta} = (h_{\theta}(x) - y)x$ $\large g = (g_{0}, g_{1}, g_{2}, ......, g_{n})$

(3). 调整 $\large \theta$

$\large \theta_{t + 1} = \theta_{t} - \alpha g_{t}$

这里的参数含义，如果不懂的，请参考机器篇——线性回归，里面有细说梯度下降

(4). 往复循环迭代 (2)、(3)两步，求出最优 $\large \theta$

8. LR 梯度下降的梯度公式推导

(1). 损失函数

$\large J(\theta) = \tfrac{1}{m} \sum_{i = 1}^{m} [-y_{i}lnh_{\theta}(x_{i}) - (1 - y_{i})ln(1 - h_{\theta}(x_{i}))]$

这里的 $\large \tfrac{1}{m}$ 是人为的均值，以使之公平，就类似求均值一样: $\large \bar{x} = \tfrac{1}{n}(x_{1}, x_{2}, x_{3}, ......, x_{n})$

(2). 求导

$\LARGE \frac{\partial J(\theta)}{\partial \theta_{j}} = \tfrac{1}{m}\frac{\partial [\sum_{i = 1}^{m}(-y_{i}lnh_{\theta}(x_{i}) - (1 - y_{i})ln(1 - h_{\theta}(x_{i})))]}{\partial \theta_{j}}$

$\LARGE = - \tfrac{1}{m} \sum_{i = 1}^{m}[y_{i}\tfrac{1}{h_{\theta}(x_{i})} \frac{\partial h_{\theta}(x_{i})}{\partial \theta_{j}} - (1- y_{i})\tfrac{1}{1- h_{\theta}(x_{i})} \frac{\partial h_{\theta}(x_{i})}{\partial \theta_{j}}]$

$\LARGE = - \tfrac{1}{m} \sum_{i = 1}^{m} (\tfrac{y_{i}}{g(\theta^T x_{i})} - \tfrac{1 - y_{i}}{1 - g(\theta^T x_{i})}) \frac{\partial g(\theta^T x_{i})}{\partial \theta_{j}}$

$\LARGE = - \tfrac{1}{m} \sum_{i = 1}^{m}(\tfrac{y_{i}}{g(\theta^T x_{i})} - \tfrac{1 - y_{i}}{1 - g(\theta^T x_{i})}) g(\theta^T x_{i}) (1 - g(\theta^T x_{i})) \frac{\partial \theta^T x_{i}}{\partial \theta_{j}}$

$\LARGE = - \tfrac{1}{m} \sum_{i = 1}^{m} (y_{i} - g(\theta^T x_{i})) x_{ij}$

$\LARGE = \tfrac{1}{m} \sum_{i = 1}^{m}(h_{\theta}(x_{i}) - y_{i})x_{ij}$

$\LARGE = \tfrac{1}{m}(h_{\theta}(x) - y)x_{j}$

即： $\LARGE \frac{\partial J(\theta)}{\partial \theta_{j}} = \tfrac{1}{m}(h_{\theta}(x) - y)x_{j}$

所以： $\LARGE \frac{\partial J(\theta)}{\partial \theta} = \tfrac{1}{m}(h_{\theta}(x) - y)x$

看到这个公式，是不是很熟悉？和线性回归的表达式一模一样。只不过，在线性回归中： $\large h_{\theta}(x) = XW$ ，在逻辑回归中： $\large h_{\theta}(x) = g(w, x)$ 。思考一下，对于其他的公式，是否梯度也等于这样一个式子呢？

9. Sigmoid 函数的优缺点

(1). 优点

①. Sigmoid 函数连续，单调递增

②. 对 Sigmoid 求导方便，导数为： $\large g'(z) = g(z)(1 - g(z))$

(2). 缺点

①. Sigmoid 反向传播时，很容易就会出现梯度消失的情况。Sigmoid 函数的有效范围在 [-4, 4]之间。

②. Sigmoid 作为激活函数，计算量很大(指数运算)

三. LR的正则化

LR也会面临特征选择和过拟合的问题，所以也需要考虑正则化。常见的有 $\large L_{1}$ 正则化和 $\large L_{2}$ 正则化。正则化详解，请参考机器篇——线性回归里面有对正则化的细说。

1. LR 的 $\large L_{1}$ 正则化

LR回归 $\large L_{1}$ 正则化的损失函数为：

$\large J(\theta) = \sum_{i = 1}^{m}(-y_{i}lnh_{\theta}(x_{i}) - (1 - y_{i})ln(1 - h_{\theta}(x_{i}))) + \alpha |\theta|_{1}$

相比普通的 LR 损失函数，增加了 $\large L_{1}$ 范数作为惩罚，超参 $\large \alpha$ 作为惩罚系数，调节惩罚项的大小， $\large |\theta|_{1}$ 为 $\large L_{1}$ 范数

2. LR的 $\large L_{2}$ 正则化

LR回归 $\large L_{2}$ 正则化的损失函数为：

$\large J(\theta) = \sum_{i = 1}^{m}(-y_{i}lnh_{\theta}(x_{i}) - (1 - y_{i})ln(1 - h_{\theta}(x_{i}))) + \alpha |\theta|_{2}^2$

四. Sigmoid 函数由来的推导(最大熵原理)

对于 Sigmoid 函数，其实很多地方都有解释这个函数为什么好，但始终没什么人给出这个玩意到底是怎么来的。下面，将推导 Sigmoid 的由来，在此，先给出结论：最大熵原理。

1. 最大熵原理

对于概率模型而言，在缺乏先验的条件的情况下，条件熵最大的模型是最好的模型

熵最大，意味着不确定程度最高，在没有先验知识的情况下，自然是最好的假设(注意，和决策树中特征选择的熵的区分)

2. 目标：条件熵最大

$\LARGE H(y|x) = - \sum_{x, y}p(x, y)lnp(y|x)$

$\LARGE = - \sum_{x, y} p(x)p(y|x)lnp(y|x)$

$\large p(x, y)$ : 为联合概率密度

$\large p(y|x)$ ：为在确定 $\large x$ 的条件下， $\large y$ 对应的概率

$\large p(x)$ ：为 $\large x$ 的概率

$\large H(y| x)$ ：为关于 $\large y$ 的条件熵

3. 对于最终的条件概率而已，所有的 label 取值概率和为 1:

$\large \sum_{y}p(y|x) = 1$

4. 定义一个特征函数： $\large f_{i}(x, y)$

由贝叶斯相关定理，对于每个特征函数 $\large i$ 而言，其期望值显眼有：

$\large \sum_{x, y}p(x, y)f_{i}(x, y) = \sum_{x, y}p(x)p(y|x)f_{i}(x, y)$

5. 拉格朗日乘子法

(1). 由于条件熵

$\large H(y|x) = - \sum_{x, y}p(x)p(y|x)lnp(y|x)$

受到 label 条件

$\large \sum_{y}p(y|x) = 1$

和特征期望函数

$\large \sum_{x, y}p(x, y)f_{i}(x, y) = \sum_{x, y}p(x)p(y|x)f_{i}(x, y)$

的束缚，所以构建(拉格朗日乘子法)：

$\large L = \sum_{x, y}p(x)p(y|x)lnp(y|x) - \lambda_{0}(\sum_{y}p(y|x) - 1) - \lambda_{1}(\sum_{x, y}p(x, y)f_{i}(x, y) - \sum_{x, y}p(x)p(y|x)f_{i}(x, y))$

函数，将问题转化为求 $\large L$ 的最小值。

(2). 此时，对 $\large L$ 求 $\large p(y|x)$ 的导数(指定 $\large x$ 和 $\large y$ ，去掉 $\large \sum$ 符号，方便求解)，并让导数为零，可得到最小值：

$\large \frac{\partial L}{\partial p(y|x)} = p(x)(lnp(y|x) + 1) - \lambda_{0} + \lambda_{1}f_{i}(x, y)p(x)$

$\large = p(x)(lnp(y|x) + 1 - \tfrac{\lambda_{0}}{p(x)} + \lambda_{1}f_{i}(x, y))$

$\large = p(x)(lnp(y|x) + 1 - \lambda_{0} + \lambda_{1}f_{i}(x, y))$

①. 由于 $\large \lambda$ 为拉格朗日参数，主要不和变量相关，加减乘除后，还是 $\large \lambda(\lambda_{0})$

②. 由于 $\large p(x) \neq 0$ ，则

$\large lnp(y|x) + 1 - \lambda_{0} + \lambda_{1}f_{i}(x, y) = 0$

即： $\large p(y|x) = e^{\lambda_{0} - 1 - \lambda_{1}f_{i}(x, y)} = e^{\lambda_{0} - \lambda_{1}f_{1}f(x, y)}$ 时， $\large L$ 有最小值

③. 由于所有的 label 概率之和为 1，则：

$\large \sum_{y}p(y|x) = \sum_{y}e^{\lambda_{0} - \lambda_{1}f_{i}(x, y)} = \tfrac{\sum_{y}e^{-\lambda_{1}f_{i}(x, y)}}{e^{-\lambda_{0}}} = 1$

令 $\large \lambda_{0} = 0$ ，有

$\LARGE p(y|x) = \tfrac{e^{-\lambda_{1}f_{i}(x, y)}}{\sum_{y}e^{-\lambda_{1}f_{i}(x, y)}}$

即得到了 softmax 函数

④. 由于 Sigmoid 函数其实是 Softmax 函数的二分类特例，而特征函数 $\large f_{i}(x, y)$ 又是自己定义的，假定 $\large y$ 的取值为 0 和 1，则可以对 $\large f_{i}(x, y)$ 定义为：

$\large f_{i}(x, y) = \left\{\begin{matrix} x & y = 1 \\ 0 & y = 0 \end{matrix}\right.$

于是有：

$\LARGE p(y|x) = \tfrac{e^{-\lambda_{1}x}}{1 + e^{-\lambda_{1}x}}$

$\LARGE = \tfrac{1}{1 + e^{\lambda_{1}x}}$

⑤. 因为 $\large p(y|x) = \tfrac{1}{1 + e^{\lambda_{1}x}}$ 式子中，已经不受 $\large y$ 的影响，所以，令 $\large z = x$ ， $\large \lambda_{1} = -1$ ， $\large g(z) = p(y|x)$ ，则

$\LARGE g(z) = \tfrac{1}{1 + e^{-z}}$

由此，得到 Sigmoid 函数。收工。

五. 代码演练

下面的代码，是直接用了 sklearn 封装的逻辑回归函数，各位大佬，如果有兴趣，也可以自己写代码实现。反正，套路和上一章：机器篇——线性回归详细介绍的梯度下降方法一样，一套撸下来就好了。不难。

#!/usr/bin/env python
# _*_ coding:utf-8 _*_
# ============================================
# @Time     : 2019/12/25 21:09
# @Author   : WanDaoYi
# @FileName : logistic_regression.py
# ============================================

import numpy as np
from sklearn import datasets
from sklearn.linear_model import LogisticRegression
import matplotlib.pyplot as plt


iris = datasets.load_iris()
print(list(iris.keys()))
print(iris["feature_names"])
# print(iris["target"])

# 获取一个数值，类似于抛硬币一样，用于对应后面的y值结果。
x = iris["data"][:, 3:]
# print(x)

# 由于 sigmoid 是二分类，所以，这里将label 做成 0,1
y = (iris['target'] == 2).astype(np.int)
# print(y)

# 有时候会报不收敛的警告，可以通过增大迭代次数来消除这个警告
logistic_reg = LogisticRegression(C=10000, multi_class='ovr', solver='sag', max_iter=1000)

logistic_reg.fit(x, y)

# 均匀获取 0~3 1000条数据，并reshape 成一列
x_new = np.linspace(0, 3, 1000).reshape(-1, 1)
# print(x_new)

# 预测目标的概率，会有两个值，如预测0的概率 9.99999999e-01 和 1 的概率 7.58488749e-10
y_proba = logistic_reg.predict_proba(x_new)

# 预测目标，根据概率来判断是否目标，只有一个结果，非 1 即 0
y_pred = logistic_reg.predict(x_new)

# print(y_proba[: 10])
# print(y_pred[: 10])

plt.plot(x_new, y_proba[:, 0], 'b--', label='Iris-Setosa')
plt.plot(x_new, y_proba[:, 1], 'r-', label='Iris-Versicolour')
plt.plot(x_new, y_pred, 'g--', label='Iris-pred')
plt.show()