逻辑函数（Logstic Function)

假设函数

代价函数（Cost Function)

梯度下降函数

背景

本文内容所使用的python包及别名：（python3.6以上)

numpy==1.18.1
pandas==0.25.3
matplotlib==3.1.2
seaborn==0.9.0

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns

逻辑回归

虽然叫回归，但它解决的是分类问题，之所以叫回归是有一些历史原因，不过怎么叫没关系。在分类问题中，逻辑回归算法是一种用的比较广泛的机器学习算法。

算法目标

区分一个样例的结果是否从属于某一个分类

举个栗子，例如有一群人，里面有黑皮肤和白皮肤的人，这些人有的是黑发，有的是金发，他们要么是非洲人，要么不是非洲人；（如下图所示的x1是皮肤的色泽，x2是头发的色泽，圆形表示非洲人，红叉表示不是非洲人）

我们训练算法来预测某个有黑/白皮肤和黑/金头发的人到底是不是非洲人，就是分类问题，而且是二分类问题。如果我们的目标是区分这个人是非洲人，还是亚洲人，还是欧洲人，这个就是三分类问题，如果有多个可能的结果，就称为多分类问题。

我们的目标是区分是不是非洲人，结果只有两种情况，是或不是，一般称“是”的结果叫积极的（positive）,称“否”的结果叫消极的（negative)，一般情况下，我们记积极的结果为1，记消极的结果为0，这个就是所谓的打标签。

接下来，我们以具体实例来演算一个逻辑回归的算法是如何进行的。

算法推演

（如果你只关心算法的实现，不关心其原理，可以直接看后面的算法实现细节；但了解算法的推演过程有助于你更好的了解算法原理，并加深对算法的理解，也使得你对于算法的优化和改进更加得心应手）

逻辑函数（Logstic Function)

假设我们仍按照上节线性回归的梯度下降算法的假设函数来处理分类问题：h(x)=theta_0+theta_1*x，那么结果会是一条直线，y的取值范围会是无穷小到无穷大，这跟我们要得到的标签值0或1不匹配。那么这时候我们引入一个sigmod函数：

$g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$

我们看它长啥样：

从上图看出，这个函数的极大值和极小值正好是标签值0和1，而且当z>=0时(横轴是z轴)，g(z)>=0.5，当z<0.5时，g(z)<0.5;如果我们将y值看作是一个概率，即结果是积极的(y=1)概率；也就是说，当我们通过假设函数计算出一个值z时，通过这个sigmoid函数就可以算出g(z),这个g(z)的意义就是我们计算出来的这个z值结果是positive的概率；以上面的例子来说的话，就是当g(z)>=0.5时，结果是积极的(y=1)的概率比较高；当g(z)<0.5时，结果是消极（y=0)的概率比较高。

Python代码：

# logistic函数
def sigmoid(z: np.ndarray) -> np.ndarray:
    return 1 / (1 + np.exp(- z))

假设函数

我们的假设函数仍使用线性回归中假设函数，不过多了一层sigmoid：

${{h}_{\theta }}\left( x \right)=\frac{1}{1+{{e}^{-{{\theta }^{T}}X}}}\\$

代价函数（Cost Function)

假如我们仍按照上节的线性回归中的代价函数来进行梯度下降的话，结果会是这个样子：

这是个非凸函数，我们看到，这种情况下我们无法得到一个costFunction的全局最小值，只会得到无数个局部最小值中的一个，我们期望的代价函数应该是这样：

我们重新定义逻辑回归中的代价函数是：

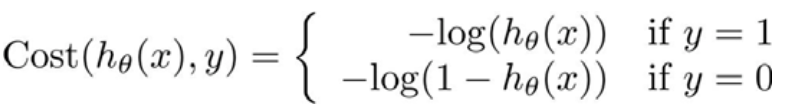
它的样子长这样：

当y=1时，如果我们算出的h_theta在0附近，代价函数的值J(theta)会非常大，我们的梯度下降为了求得J(theta)的最小值得到参数值theta，所以通过不断的迭代计算，我们最终能得到最小的h(theta)的取值等于1时，就是我们所要的theta参数。类似地在y=0时，在h(theta)=1时取得代价函数J(theta)的最小值。

也就是说，当y=1时，当代价函数J(theta)=0时，h(theta)的值=1；当y=0时，当代价函数J(theta)=0时，h(theta)的值=0；

我们可以把它写成一个函数表达式：（在此不在证明，有兴趣的可以推导一下）

$Cost\left( {h_\theta}\left( x \right),y \right)=-y\times log\left( {h_\theta}\left( x \right) \right)-(1-y)\times log\left( 1-{h_\theta}\left( x \right) \right)$

于是我们得到最终的代价函数：

$J\left( \theta \right)=-\frac{1}{m}\sum\limits_{i=1}^{m}{[{{y}^{(i)}}\log \left( {{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)+\left( 1-{{y}^{(i)}} \right)\log \left( 1-{{h}_{\theta }}\left( {{x}^{(i)}} \right) \right)]}$

Python代码：

# 代价函数,注意为了使用scipy的最小化拟合方法,必须定义代价函数的第一个参数为theta,后续参数可以自定义
def cost_function(theta: np.ndarray, X: np.ndarray, y: np.ndarray) -> np.float:
    # @ 是矩阵乘法,同np.dot(A,B)
    # 在X @ theta中,例如X是(100,3)的ndarray, theta是(100,)的ndarray列表,得到g_x为(100,)的ndarray一维数组列表
    g_x = sigmoid(X @ theta)
    return np.mean(-y * np.log(g_x) - (1 - y) * np.log(1 - g_x))

有了这个代价函数，我们接下来就可以进行编码计算了。

梯度下降函数

$\frac{\partial J\left( \theta \right)}{\partial {{\theta }_{j}}}=\frac{1}{m}\sum\limits_{i=1}^{m}{({{h}_{\theta }}\left( {{x}^{(i)}} \right)-{{y}^{(i)}})x_{_{j}}^{(i)}}$

$=\frac{1}{m} X^T( Sigmoid(X\theta) - y )$

这里的梯度下降函数跟线性回归中很像，但是由于我们定义的假设函数不一样，实际上它们是完全不同的

算法实现

案例

现在有一个学生考试成绩表，包含了两次考试的成绩，以及这个学生是否通过了考试；数据长这个样子：

x1是第一次考试成绩，x2是第二次考试成绩，y是这位同学是否通过考试，1表示通过，0表示不通过；

（这个数据集中有100位考生，下表只列出了前10位同学的信息；这个数据集可以在文后的附件中ex2data1.txt下载）

统计信息如下，这个数据集有100行，3列，x1和x2的值范围约在30-100之间

实际的数据散点图：

我们的目标是找出两次考试与学生是否通过的关系

案例分析及代码实现

读取数据

首先我们需要从ex2data1.txt读出我们需要的数据，返回值类型是pandas的DataFrame类型，我们需要把它转换成矩阵方便以后的计算

# 读取数据,x1是第一次考试的评分,x2是第二次考试的评分,y是标签值是否通过
def read_data(data_file: str) -> pd.DataFrame:
    return pd.read_csv(data_file, header=None, names=['x1', 'x2', 'y'])

特征选择

这里直接使用原特征，将原数据转换成矩阵；X是特征集，y是标签值；X是100*3的矩阵，y是100*1的矩阵

# 读取特征,返回的X的类型必须是ndarray
def get_X(df: pd.DataFrame) -> np.ndarray:
    # 在此不要改变原数据的内容,不要直接在原数据中插入新列
    dfc = df.iloc[:, :-1]
    # 在首列插入对应于theta_0的x_0列
    dfc.insert(0, 'x0', 1)
    return np.array(dfc)

# 读取标签
def get_y(df: pd.DataFrame) -> np.ndarray:
    # 取最后一列的标签值作为y
    return np.array(df.iloc[:, -1])

注意y的形状是(100,)

看下我们得到的X和y:

参数theta定义

接下来定义好我们的参数theta:

# 定义theta,theta的大小与我们的假设函数有关
# 在此假定我们的假设函数是一个一元多次方程,theta列的大小比所有x多一列,正好是原数据的列数
theta = np.zeros(data.shape[1])  # X(m*n), X是m行n列的矩阵,theta是n*1的向量

我们初始化的theta:

代价函数

定义代价函数和signmoid函数：

# logistic函数
def sigmoid(z: np.ndarray) -> np.ndarray:
    return 1 / (1 + np.exp(- z))

# 代价函数,注意为了使用scipy的最小化拟合方法,必须定义代价函数的第一个参数为theta,后续参数可以自定义
def cost_function(theta: np.ndarray, X: np.ndarray, y: np.ndarray) -> np.float:
    # @ 是矩阵乘法,同np.dot(A,B)
    # 在X @ theta中,X是(100,3)的ndarray, theta是(100,)的ndarray列表,得到g_x为(100,)的ndarray一维数组列表
    g_x = sigmoid(X @ theta)
    return np.mean(-y * np.log(g_x) - (1 - y) * np.log(1 - g_x))

梯度下降

定义梯度下降函数：

# 梯度下降
def gradient_descent_function(theta: np.ndarray, X: np.ndarray, y: np.ndarray) -> np.ndarray:
    g_x = sigmoid(X @ theta)
    return (1 / len(X)) * X.T @ (g_x - y)

最小化拟合

最后是最小化代价函数，最小化拟合。我们可以自定义学习率alpha,一步步地减小代价函数值以求得参数，但是实际上一些科学计算库里已经提供了最小化代价函数的api，而且它们做了优化，能以更少的步数或者说更快地找到使得代价函数最小的theta参数值，所以我们直接使用即可。

这里需要注意的是，要使用以面这个scipy的optimize最小化拟合方法，在定义梯度下降函数gradient_descent_function时，gradient_descent_function的第一个参数必须是theta，theta的类型必须是一个列表结构；如果你的梯度下降函数中，除了X和y外还需要额外的参数，必须在opt.minimize的args参数里也传进去才能生效。

# 最小化代价函数,使用scipy库中的梯度下降法,令其自动选择学习率来寻找我们要找的使代价函数最小的参数
# scipy文档:http://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.minimize.html#scipy.optimize.minimize
def minimize(theta: np.array, X: np.array, y: np.array):
    import scipy.optimize as opt
    res = opt.minimize(fun=cost_function, x0=theta, args=(X, y), method='Newton-CG', jac=gradient_descent_function)
    return res  # res.x=[-25.16227358,   0.20623923,   0.20147921]不同的计算机可能有误差,误差在1%内可接受

主函数

最后是主函数，分步调用以求得theta:

    # 读取数据, 最后一列是标签值
    data = read_data('ex2data1.txt')

    X = get_X(data)  # X是(100,3)的二维ndarray对象
    y = get_y(data)  # y是含有100个元素的一维ndarray对象

    # 定义theta,theta的大小与我们的假设函数有关
    # 在此假定我们的假设函数是一个一元多次方程,theta列的大小比所有x多一列,正好是原数据的列数
    theta = np.zeros(data.shape[1])  # X(m*n), X是m行n列的矩阵,theta是n*1的向量

    # 看一下第一次计算代价函数和梯度下降函数的值,由于初始化theta都是0,所以"X@theta"结果都是0
    cost_val = cost_function(theta, X, y)  # 0.69314718055994529
    gradient_val = gradient_descent_function(theta, X, y)  # [ -0.1 , -12.00921659, -11.26284221]

    # 调用最小化拟合函数
    result = minimize(theta, X, y)
    print(result)

最终计算得到的result:

result.x就是我们要得到的theta值

结果验证

评估报告：（调和平均值在88%左右，已经很不错了）

图形化展示

我们求得的函数图形化表示如下：（关于验证的相关代码在附件中可查看）

本文数据及代码案例

如果还想了解其它有关机器学习的知识，可以查看作者的《机器学习目录》

（本文所有的数据和代码在附件中都有）

【机器学习】三、逻辑回归(Logistic Regression)

背景

逻辑回归

算法目标

算法推演

逻辑函数（Logstic Function)

假设函数

代价函数（Cost Function)

梯度下降函数

算法实现

案例

案例分析及代码实现

读取数据

特征选择

参数theta定义

代价函数

梯度下降

最小化拟合

主函数

结果验证

图形化展示

猜你喜欢