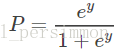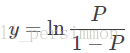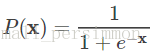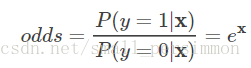算法学习——逻辑回归(Logistic Regression)

1.Logistic Regression

1.1什么是回归？

英文单词Regression翻译成中文“回归”，那什么是回归呢？事实上，在Logistic回归出现以前，人们最先引入的是线性回归。了解二者之间的来龙去脉将帮助你更深刻地认识Logistic回归。

回归一词最早由英国科学家弗朗西斯·高尔顿（Francis Galton）提出，他还是著名的生物学家、进化论奠基人查尔斯·达尔文（Charles Darwin）的表弟。高尔顿深受进化论思想的影响，并把该思想引入到人类研究，从遗传的角度解释个体差异形成的原因。

高尔顿发现，虽然有一个趋势——父母高，儿女也高；父母矮，儿女也矮，但给定父母的身高，儿女辈的平均身高却趋向于或者“回归”到全体人口的平均身高。换句话说，即使父母双方都异常高或者异常矮，儿女的身高还是会趋向于人口总体的平均身高。这也就是所谓的普遍回归规律。

高尔顿的这一结论被他的朋友，英国数学家、数理统计学的创立者卡尔·皮尔逊（Karl Pearson）所证实。皮尔逊收集了一些家庭的1000多名成员的身高记录，发现对于一个父亲高的群体，儿辈的平均身高低于他们父辈的身高；而对于一个父亲矮的群体，儿辈的平均身高则高于其父辈的身高。这样就把高的和矮的儿辈一同“回归”到所有男子的平均身高，用高尔顿的话说，这是“回归到中等”。

回归分析是被用来研究一个被解释变量（Explained Variable）与一个或多个解释变量（Explanatory Variable）之间关系的统计技术。被解释变量有时也被称为因变量（Dependent Variable），与之相对应地，解释变量也被称为自变量（Independent Variable）。回归分析的意义在于通过重复抽样获得的解释变量的已知或设定值来估计或者预测被解释变量的总体均值。

如果你对上面这段话感到困惑，不妨来看看下面这张图。图上有一些观测到的样本点，线性回归的任务就在于通过一条线来最大程度地拟合这些点。例如，我们已经得到了一些父辈与儿辈身高的数据，而且我们认为儿辈的身高在很大程度上依赖于父辈的身高。那么，我们就可以把儿辈身高看成是被解释变量（即图中的纵轴），把父辈身高看成是解释变量（即图中的衡轴）。然后通过一条回归线来拟合这些数据，如此一来，当我们已知一个父亲的身高时，就可以通过回归线所表现出来的线性关系推测出儿子身高的大概水平。

在线性回归中，我们假设被解释变量 $y$ 与解释变量 $x_{1},x_{2},$ $\cdots$ $,x_{n}$ 之间具有线性相关的关系，那么用公式就可以将线性回归模型表示为

其中 $w_{0}$ 表示常数项，上图中因为自变量只有一个，所以一元线性回归的公式表示应该是 $y = w_{0} + w_{1}x$ ，显然它是多元线性回归模型中最简单的情况。

1.2Logistic的引入

已经掌握了线性回归的基本内容。现在我们来看一个稍微有点变化的例子。

扫描二维码关注公众号，回复： 3910545 查看本文章

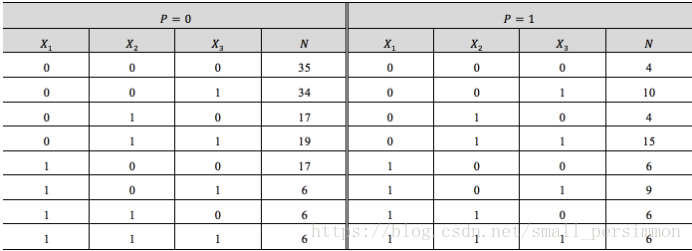
为研究与急性心肌梗塞急诊治疗情况有关的因素，现收集了200个急性心肌梗塞的病例，如下表所示。其中， $X_{1}$ 用于指示救治前是否休克， $X_{1} = 1$ 表示救治前已休克， $X_{1} = 0$ 表示救治前未休克； $X_{2}$ 用于指示救治前是否心衰， $X_{2} = 1$ 表示救治前已发生心衰， $X_{2} = 0$ 表示救治前未发生心衰； $X_{3}$ 用于指示12小时内有无治疗措施， $X_{3} = 1$ 表示没有，否则 $X_{3} = 0$ 。最后给出了病患的最终结局，当 $P = 0$ 时，表示患者生存；否则当 $P = 1$ 时，表示患者死亡。

如果要建立回归模型，进而来预测不同情况下病患生存的概率，考虑用多重回归来做，（注意我们将大写换成了小写）即

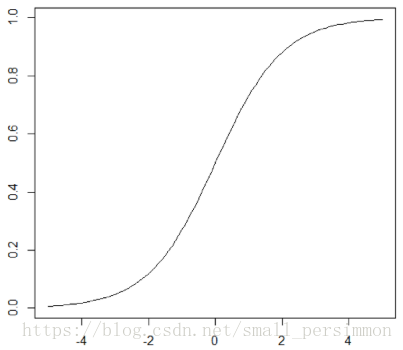
则显然将自变量带入上述回归方程，不能保证概率 $P$ 一定位于0～1。于是想到用Logistic函数将自变量映射至0～1。Logistic函数的定义如下：

或

其函数的图像如图下所示。

然后上面的函数定义式将多元线性回归中的因变量替换得到

其中，而且在我们当前所讨论的例子中 $n = 3$ 。
上式中的 $w_{0},w_{1}$ ,⋯, $w_{n}$ 正是我们要求的参数，通常采用极大似然估计法对参数进行求解。对于本题而言则有

进而有（β 就是我们所讨论的参数 $w$ ）

当我们得到上面最后一个公式的时候，如果再有一组观察样本，将其带入公式，就可以算得病人生存与否的概率。
以上我们就通过了一个例子向读者演示了如何从原始的线性回归演化出Logistic回归。而且，不难发现，Logistic回归可以用作机器学习中的分类器。当我们得到一个事件发生与否的概率时，自然就已经得出结论，其到底应该属于“发生”的那一类别，还是属于“不发生”的那一类别。

接下来我们要从整个具体的例子中抽象出Logistic回归的一般化过程。并为后续一些文章的讨论埋下伏笔。

所谓机器学习，最终是让机器自己学到一个可以用于问题解决的模型。而这个模型本质上是由一组参数定义的，也就是前面讨论的 $w_{0},w_{1}$ ,⋯, $w_{n}$ 。在得到测试数据时，将这组参数（在Logistic回归中也可以认为是权值）与测试数据线性加和得到

这里 $x_{1},x_{2},$ ⋯ $,x_{n}$ 是每个样本的 $n$ 个特征。之后再按照Logistic函数的形式求出

在给定特征向量时，条件概率为根据观测量某事件 $y$ 发生的概率。那么Logistic回归模型可以表示为

相对应地，在给定条件 $x$ 时，事件 $y$ 不发生的概率为

而且还可以得到事件发生与不发生的概率之比为

这个比值称为事件的发生比。

概率论的知识告诉我们参数估计时可以采用最大似然法。假设有 $m$ 个观测样本，观测值分别为 $y_{1},y_{2}$ ,⋯, $y_{m}$ ，设为给定条件下得到 $y_{i} = 1$ 的概率。同样地， $y_{i} = 0$ 的概率为，所以得到一个观测值的概率为。

各个观测样本之间相互独立，那么它们的联合分布为各边缘分布的乘积。得到似然函数为

然后我们的目标是求出使这一似然函数值最大的参数估计，于是对函数取对数得到

根据多元函数求极值的方法，为了求出使得最大的向量，对上述的似然函数求偏导后得到

现在，我们所要做的就是通过上面已经得到的结论来求解使得似然函数最大化的参数向量。在实际中有很多方法可供选择，其中比较常用的包括梯度下降法、牛顿法和拟牛顿法等。

2.Softmax回归

softmax回归

3. LogisticRegression 参数说明

官方英文文档详解

class sklearn.linear_model.LogisticRegression(penalty=’l2’, dual=False, 
tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, 
random_state=None,solver=’liblinear’, max_iter=100, multi_class=’ovr’, 
verbose=0, warm_start=False, n_jobs=1)[source]

参数说明：

OvO OvR MvM区别与联系

参考文章：

机器学习之详解Logistic回归

《机器学习西瓜书》学习笔记——第三章_线性模型：逻辑回归