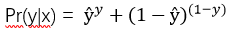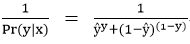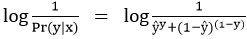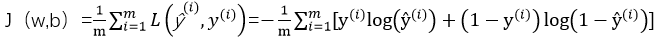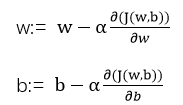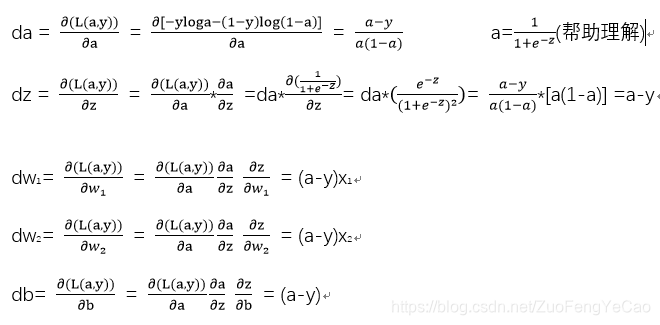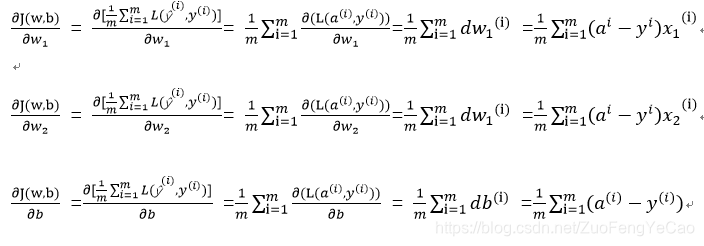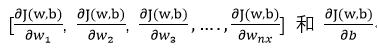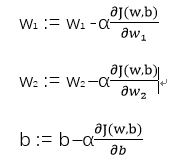Logistic Regression:是一种分类算法,即对于一个样本判断其为真或假.
Logistic Regression是以线性回归为基础,所以基础方程:y=wx+b
样本数据: {(x(1),y(1)), (x(2),y(2)), (x(3),y(3))…(x(m),y(m))} ,即x∈Rnx , y∈(0,1)
一个样本数据可能是含有nx个特征向量:x(i)={x1(i),x2(i), x3(i),xn(i)} (实际上是n维的列向量),称为一个colume,则所有的输入样本集可以组成一个X=[n,m]的矩阵。
W为特征的影响因子,{θ1, θ2, θ3,… θn},或者表示为{θ0, θ1, θ2, θ3,… θn},其中θ0=b。则对于一个样本的预测值ŷ=x1θ1+ x2θ2+ x3θ3+…xnθn+b,多个样本可以表示为矩阵形式ŷ(i)=WTX(i)+b (T表示transpose)
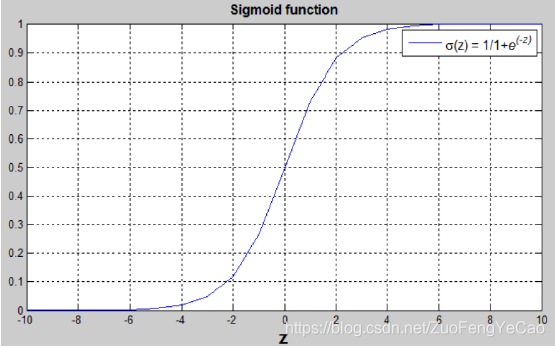
ŷ(i)判断作为判断样本是否为真的依据,可以表示为在给定输入x的条件下判断样本y=1的概率,即Pr(y=1|x),而概率的取值范围为(0,1),ŷ(i)=WTX(i)+b是可能为正值,也可能为负值,因此需要引入一个激活函数来限制输出范围,这个激活函数一般选择sigmoid函数σ(z)=1/(1+e^(-z) ),其函数图如下:
经过激活函数处理后的ŷ(i)=σ(WTX(i)+b)= 1/(1+e(-(WT X^i+b)) )
对于样本数据来说,模型评估预测值ŷ与真实值y的存在差距,要评估此差距的大小就需要引入loss function,L(ŷ,y),loss function的种类:
1. MSE :Minimum Squared Error
L(ŷ,y)= 1/2*(ŷ-y)^2 , 但是存在弊端,non-convex,即非凸函数,有局部极小值,但没有全局的最小值。
2. Logarithmic Function
由前面的定义我们知道ŷ =Pr(y=1|x),则预测的准确率表示为Pr(y|x) ,有
当y=1时,Pr(y|x) = ŷ ;
当y=0时,Pr(y|x) = 1-ŷ;
综合为一条公式 :
注意到概率越大,说明误差越小,则误差可以表示为:
同时为构造方便计算的loss function,取对数形式
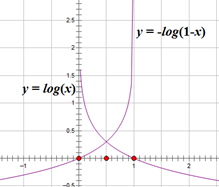
即L(ŷ,y)=-[ylog(ŷ)+(1-y) log(1-ŷ)] ,其函数图像如下:
当y=1时,L(ŷ,y)=-log(ŷ);ŷ取值(0,1)之间,要使用预测误差L 足够小,要求预测值ŷ足够大,无限接近于1;
当y=0时,L(ŷ,y)=-log(1-ŷ);ŷ取值(0,1)之间,要使用预测误差L 足够小,要求预测值ŷ足够小,无限接近于0;
即是说,每个样本的预测误差L越小,预测结果ŷ越接近真实结果y。
Cost Function : Loss Function是单个样本的误差,Cost Function是总样本的平均误差,目的是寻找一个参数对(W,b)来使平均误差最小,做最优拟合,所以Cost Function函数的变量变成了(W,b),定义如下:
梯度下降法(Gradient Descent)
我们的目标是寻找一个参数对(W,b)使得J(W,b)最小,梯度就是偏导数,即函数线上任意一个点的斜率。
梯度下降法的原理如下:
为方便说明先假设w跟b都是一个单一实数,而且J(w,b)是一个凸函数(Loss function变形后成为一个凸函数),
分别表示w与b进行一次梯度计算后的更新值,对于凸函数来说,如下图所示,在最低点的左边,函数斜率小于0,所以α(∂(J(w,b))/∂w<0,w:>w,新的w值变大,向横坐标轴右移。反之,在最低点右侧,函数斜率大于0,α(∂(J(w,b))/∂w>0 w:<w,向左移。α调节移动步伐的大小。级过多次迭代,J(w,b)会越来越靠近最小值。
同时,凸函数的好处是越靠近最小值时斜率越接近于0,我们可以设定一个阈值,当梯度(斜率)小于该阈值时判断当前(W,b)为最优解。
Back Propogation (反向传播)
以上已经介绍完logistic regression 的基本原理,下面分析下实现过程:
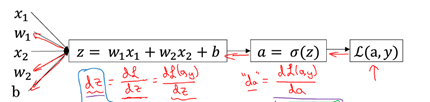
我们假设每一个样本有为两个特征向量,则根据前面介绍可以分解为下图的步骤。back propogation (反向传播)方法实际上就是多级函数求偏导数的链式规则。
对于一个样本,参数(W,b)对Cost Function L(a,y) 的梯度如下:
对于m个样本,参数(W,b)对Cost Function 的梯度如下:
由此可见,求一个特征的梯度需要i 从 1到m(总样本数)循环一遍;
对于拥有n个维度特征向量样本来说,还需要循环n次,求出各向量因子的梯度
我们的目标是让Cost Function结果往最小值方向移,由此需要更新参数,进行多次迭代计算,此过程中这些梯度会越来越小,直至达到我们设定的门限:
缺陷:
在以上步骤我们看到,一共需要三次大循环:
-
计算一个特征向量的梯度需要遍历所有样本数据;
-
样本特征向量有n维,需要循环n次,求出每个特征向量的梯度;
-
循环进行梯度下降迭代,直到找到最优解。
Vectorization (向量化) :
在实际应用过程中,我们应尽量避免使用for循环来实现,例如可以使用python numpy库里的dot(点乘函数) ,使用的是并行处理的机制SIMD(single instruction multiple data ),提高运算速率
- 本文配合吴恩达教学视频食用效果更佳*
https://study.163.com/my#/smarts