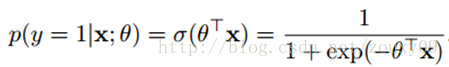逻辑回归

1. 问题

实际工作中，我们可能会遇到如下问题：

预测一个用户是否点击特定的商品
判断用户的性别
预测用户是否会购买给定的品类
判断一条评论是正面的还是负面的

这些都可以看做是分类问题，更准确地，都可以看做是二分类问题。

2. 模型

2.1 sigmoid 函数

在介绍逻辑回归模型之前，我们先引入sigmoid函数，其数学形式是：

$g(x) = \frac{1}{1+e^{-x}}$

对应的函数曲线如下图所示：

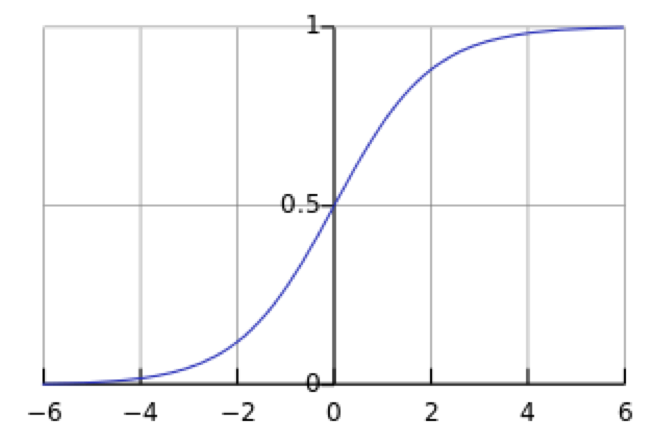
2.2 决策函数

设x是m维的样本特征向量(input)；y是标签label，为正例和负例。这里θ是模型参数，也就是回归系数，σ是sigmoid函数。则该样本是正例的概率为：

对于二分类来说，可以简单的认为：如果样本x属于正类的概率大于0.5，那么就判定它是正类，否则就是负类。

2.3 参数求解

模型的数学形式确定后，剩下就是如何去求解模型中的参数 $\theta$ 。统计学中常用的一种方法是最大似然估计，即找到一组参数，使得在这组参数下，我们的数据的概率越大。

假设我们有n个独立的训练样本{(x1, y1) ,(x2, y2),…, (xn, yn)}，y={0, 1}。那每一个观察到的样本(xi, yi)出现的概率是：

这是因为当 $y_i = 1$ 时，该概率为 $P(y_i = 1|x_i)$ ; 当 $y_i = 0$ 时，该概率为 $1- P(y_i = 1| x_i)$ .

所有样本{(x1, y1) ,(x2, y2),…, (xn, yn)}出现的概率总和为：

取对数，得到：

$log(L(\theta)) = \sum y_i* logP(y_i = 1|x_i)+ (1-y_i)*log(1-P(y_i = 1|x_i))\\ ~~~~~~~~~~~~~~~~~= \sum y_i *log\sigma(\theta^Tx)+(1-y_i)log(1-\sigma(\theta^Tx))$

这时候，用L(θ)对θ求导,得到：

$\frac{\partial ln L(\theta)}{\partial \theta} = \sum_{i=1}^n (y_i - \sigma(\theta^T x_i)) x_i$

然后令该导数为0，你会很失望的发现，它无法解析求解。所以只能借助梯度下降算法来进行迭代。

2.4 迭代求解

某一个样本 $(x_i, y_i)$ 为正例的概率为 $\sigma(\theta^Tx)$ , 为负例的概率为 $1- \sigma(\theta^Tx)$ .

这一个样本的交叉熵损失函数(log 损失)为：

$l(\theta) = -y_i log(\sigma(\theta^T x))-(1-y_i)log(1-\sigma(\theta^Tx))$

对这一个样本做梯度下降：

$\theta^{t+1} = \theta^t - \alpha \frac{\partial l(\theta)}{\partial \theta} = \theta^t - \alpha (y_i - \sigma(\theta^T x_i))x_i$

如果取整个数据集上的平均log损失，我们可以得到

$J(\theta) = \frac{1}{N} \sum l(\theta)$

即在逻辑回归模型中，我们最大化似然函数和最小化log损失函数实际上是等价的。

2.5 并行化

如果用随机梯度下降，每次只能使用一个样本参与迭代，这样遍历数据集的速度太慢了。所以，使用小批量梯度下降来并行化，每次取m个样本并行做梯度下降。

LR的一个很重要的好处就是它能够并行化，在工程中效率很高。

$\theta^{t+1} = \theta^t - \alpha \frac{\partial \sum_{i=1}^m l_i(\theta)}{\partial \theta} = \theta^t - \alpha \sum_{i=1}^m (y_i - \sigma(\theta^T x_i))x_i$

Q/A

Q1: LR与线性回归的区别与联系

线性回归的优化目标函数是最小二乘，而逻辑回归则是似然函数
线性回归在整个实数域范围内进行预测，逻辑回归则减小预测范围，将预测值限定为[0,1]间。

Q2: 连续特征的离散化：在什么情况下将连续的特征离散化之后可以获得更好的效果？最近刚接触CTR预估，发现CTR预估一般都是用LR，而且特征都是离散的。为什么一定要用离散特征呢？这样做的好处在哪里？

A2: 在工业界，很少直接将连续值作为逻辑回归模型的特征输入，而是将连续特征离散化为一系列0、1特征交给逻辑回归模型，这样做的优势有以下几点：

离散特征的增加和减少都很容易，易于模型的快速迭代；
稀疏向量内积乘法运算速度快，计算结果方便存储，容易扩展；
离散化后的特征对异常数据有很强的鲁棒性：比如一个特征是年龄>30是1，否则0。如果特征没有离散化，一个异常数据“年龄300岁”会给模型造成很大的干扰；
逻辑回归属于广义线性模型，表达能力受限；单变量离散化为N个后，每个变量有单独的权重，相当于为模型引入了非线性，能够提升模型表达能力，加大拟合；
离散化后可以进行特征交叉，由M+N个变量变为M*N个变量，进一步引入非线性，提升表达能力；
特征离散化后，模型会更稳定，比如如果对用户年龄离散化，20-30作为一个区间，不会因为一个用户年龄长了一岁就变成一个完全不同的人。当然处于区间相邻处的样本会刚好相反，所以怎么划分区间是门学问；
特征离散化以后，起到了简化了逻辑回归模型的作用，降低了模型过拟合的风险。

简单说，模型是使用离散特征还是连续特征，其实是一个“海量离散特征+简单模型” 同 “少量连续特征+复杂模型”的权衡。既可以离散化用线性模型，也可以用连续特征加深度学习。就看是喜欢折腾特征还是折腾模型了。

延伸

生成模型和判别模型

preview

判别式模型举例：要确定一个羊是山羊还是绵羊，用判别模型的方法是从历史数据中学习到模型，然后通过提取这只羊的特征来预测出这只羊是山羊的概率，是绵羊的概率。

生成式模型举例：利用生成模型是根据山羊的特征首先学习出一个山羊的模型，然后根据绵羊的特征学习出一个绵羊的模型，然后从这只羊中提取特征，放到山羊模型中看概率是多少，在放到绵羊模型中看概率是多少，哪个大就是哪个。

逻辑回归是一种判别模型，表现为直接对条件概率P(y|x)建模，而不关心背后的数据分布P(x,y)。

判别式模型常见的主要有：

　　　　Logistic Regression

　　　　SVM

　　　　Traditional Neural Networks

　　　　Nearest Neighbor

　　　　CRF

　　　　Linear Discriminant Analysis

　　　　Boosting

　　　　Linear Regression

产生式模型常见的主要有：

Gaussians

Naive Bayes

Mixtures of Multinomials

Mixtures of Gaussians

Mixtures of Experts

HMMs

　　　　Sigmoidal Belief Networks, Bayesian Networks

　　　　Markov Random Fields

　　　　Latent Dirichlet Allocation

参考资料：

https://blog.csdn.net/zouxy09/article/details/20319673

机器学习 - 逻辑回归 Logistic Regression

逻辑回归

1. 问题

2. 模型

Q/A

延伸

生成模型和判别模型

猜你喜欢