【机器学习】逻辑斯蒂回归（Logistic Regression）详解

引言

LR回归，虽然这个算法从名字上来看，是回归算法，但其实际上是一个分类算法，学术界也叫它logit regression, maximum-entropy classification (MaxEnt)或者是the log-linear classifier。在机器学习算法中，有几十种分类器，LR回归是其中最常用的一个。

logit和logistic模型的区别:

二者的根本区别在于广义化线性模型中的联系函数的形式。logit采用对数形式 $log(p)$ ，logistic形式为 $log({p\over1-p})$ 。

当因变量是多类的，可以采用logistic，也可以用logit，计算结果并无多少差别。

LR回归是在线性回归模型的基础上，使用 $sigmoid$ 函数，将线性模型 $w^Tx$ 的结果压缩到 $[0,1]$ 之间，使其拥有概率意义。其本质仍然是一个线性模型，实现相对简单。在广告计算和推荐系统中使用频率极高，是CTR预估模型的基本算法。同时，LR模型也是深度学习的基本组成单元。

LR回归属于概率性判别式模型，之所谓是概率性模型，是因为LR模型是有概率意义的；之所以是判别式模型，是因为LR回归并没有对数据的分布进行建模，也就是说，LR模型并不知道数据的具体分布，而是直接将判别函数，或者说是分类超平面求解了出来。

一般来说，分类算法都是求解 $p(C_k|x)$ ，即对于一个新的样本，计算其条件概率 $p(C_k|x)$ 。这个可以看做是一个后验概率，其计算可以基于贝叶斯公式得到： $p(C_k|x)={p(x|C_k)p(C_k) \over \sum_{k=1}^K p(x|C_k)p(C_k)}$ ,其中 $p(x|C_k)$ 是类条件概率密度， $p(C_k)$ 是类的概率先验。使用这种方法的模型，称为是生成模型，即： $p(C_k|x)$ 是由 $p(x|C_k)$ 和 $p(C_k)$ 生成的。

分类算法所得到的 $p(C_k|x)$ 可以将输入空间划分成许多不相交的区域，这些区域之间的分隔面被称为判别函数（也称为分类面），有了判别函数，就可以进行分类了，上面生成模型，最终也是为了得到判别函数。如果直接对判别函数进行求解，得到判别面，这种方法，就称为判别式法。LR就属于这种方法。

logistic distribution （逻辑斯蒂分布）

之前说过，LR回归是在线性回归模型的基础上，使用 $sigmoid$ 函数得到的。关于线性模型，在前面的文章中已经说了很多了。这里就先介绍一下， $sigmoid$ 函数。

首先，需要对 logistic distribution （逻辑斯蒂分布）进行说明，这个分布的概率密度函数和概率分布函数如下：

$p(x;\mu,s)=\frac{e^{-{x-\mu \over s}}}{s(1+e^{-{x-\mu \over s}})^2}$

$P(x;\mu,s)=\frac{1}{1+e^{-{x-\mu \over s}}}$

这里 $\mu$ 是位置参数，而 $s$ 是形状参数。

扫描二维码关注公众号，回复： 3680508 查看本文章

逻辑斯蒂分布在不同的 $\mu$ 和 $s$ 的情况下，其概率密度函数 $p(x;\mu,s)$ 的图形：

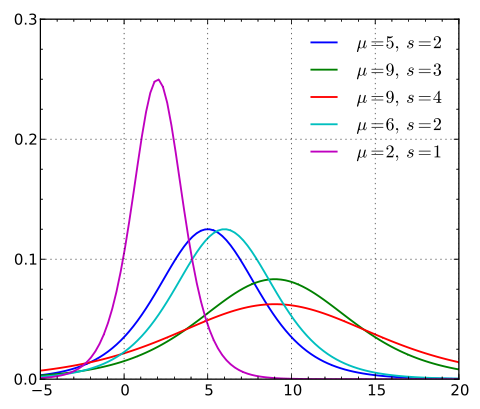
480px-Logisticpdfunction.svg.png-45.2kB — 概率密度函数

逻辑斯蒂分布在不同的 $\mu$ 和 $s$ 的情况下，其概率分布函数 $p(x;\mu,s)$ 的图形：

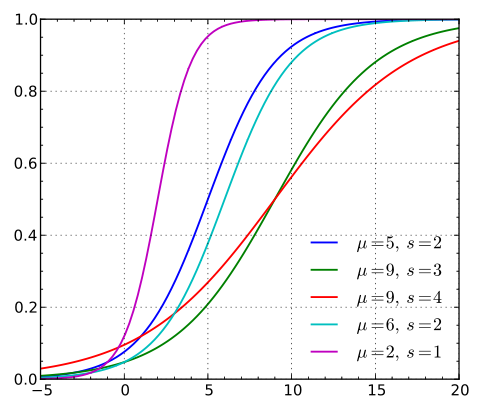
480px-Logistic_cdf.svg.png-49.9kB — 概率分布函数（累积密度函数）

由图可以看出，逻辑斯蒂分布和高斯分布的密度函数长得差不多。特别注意逻辑斯蒂分布的概率密度函数自中心附近增长速度较快，而在两端的增长速度相对较慢。形状参数 $s$ 的数值越小，则概率密度函数在中心附近增长越快。

当 $\mu=0,s=1$ 时，逻辑斯蒂分布的概率分布函数（累计密度函数）就是我们常说的 $sigmoid$ 函数：

$\sigma(p)=\frac{1}{1+e^{-p}}$

且其导数为：

$\frac{d\sigma}{dp}=\sigma(1-\sigma)$

这是一个非常好的特性，并且这个特性在后面的推导中将会被用到。

从逻辑斯蒂分布到逻辑斯蒂回归模型

前面说过，分类算法都是求解 $p(C_k|x)$ ，而逻辑斯蒂回归模型，就是用当 $\mu=0,s=1$ 时的逻辑斯蒂分布的概率分布函数： $sigmoid$ 函数，对 $p(C_k|x)$ 进行建模，所得到的模型，对于二分类的逻辑斯蒂回归模型有：

$P(C_1|x)=\frac{P(x|C_1)P(C_1)}{P(x|C_1)P(C_1) + P(x|C_2)P(C_2)}= \sigma(p)=\frac{1}{1+e^{-p}}$

$P(C_2|x)=\frac{P(x|C_2)P(C_2)}{P(x|C_1)P(C_1) + P(x|C_2)P(C_2)}= 1-\sigma(p)=\frac{e^{-p}}{1+e^{-p}}$

很容易求得，这里：

$p=ln\frac{P(x|C_1)P(C_1)}{P(x|C_2)P(C_2)}$

这里 $p$ 又可以被称作 $odds$ 比值比，又名机会比、优势比。（符号标记不慎，这里的 $p$ 标记其实并不太合适。）

$p$ 就是我们在分类算法中的决策面，由于LR回归是一个线性分类算法，所以，此处采用线性模型：这里参数向量为 $\omega=\{w_{0},w_{1},w_{2},...,w_{n}\}$ ， $\phi_{j}(x)$ 是线性模型的基函数，基函数的数目为 $M$ 个，如果定义 $\phi_{0}(x)=1$ 的话。

$h_\omega(x)=p=y(x,w)=\sum _{j=0}^M\omega_j\phi_j(x)=\omega^T\Phi(x)$

$w=(w_{0},w_{1},w_{2},...,w_{M})$

$\phi=(\phi_{0},\phi_{1},\phi_{2},...,\phi_{M})$

在这里的 $p$ 其实就是 $h_\omega(x)$ （Hypothesis）。

那么，逻辑斯蒂回归模型 $p(C_k|x)$ 就可以重写为下面这个形式：

$p(C_1|x)=\sigma(h_\omega(x))=\sigma(\omega^T\Phi(x))$

$p(C_2|x)=1-\sigma(h_\omega(x))=1-\sigma(\omega^T\Phi(x))$

对于一个二分类的数据集 $\{x_n,t_n\}$ ，这里 $t_n\in\{0,1\}$ ， $\phi_n=\phi(x_n),t=\{t_1,t_2,...,\},y_n=p(C_1|x_n)$ 其极大似然估计为：

$P(t|w)=P(t;w)=\prod_{n=1}^N\{y_n^{t_n}*(1-y_n)^{(1-t_n)}\}$

竖线改分号只是为了强调在这种情形下，它们含义是相同的，具体可见极大似然估计

对数似然估计为：（通常我们会取其平均 ${1\over N}$ ）

$lnP(t|w)=\sum_{n=1}^N\{t_nlny_n+(1-t_n)ln(1-y_n)\}$

关于 $w$ 的梯度为：

$\frac{\partial lnP(t|w)}{\partial w}=\sum_{n=1}^N \left [t_nlny_n+(1-t_n)ln(1-y_n) \right ]$

$\begin{aligned} \frac{\partial lnP(t|w)}{\partial w} &= \sum_{n=1}^N\{t_n\frac{1}{y_n}\partial y_n-(1-t_n)\frac{1}{1-y_n}\partial y_n\}\\ &=\sum_{n=1}^N\{(t_n\frac{1}{y_n}-(1-t_n)\frac{1}{1-y_n})y_n(1-y_n)\partial(-w^T\phi_n)\}\\ &=\sum_{n=1}^N\{(y_n-t_n)\phi_n\} \end{aligned}$

得到梯度之后，那么就可以和线性回归模型一样，使用梯度下降法求解参数 $w$ 。

$w_{t+1}=w_t-\alpha \nabla_\omega lnP(t|w)$

梯度下降法实现相对简单，但是其收敛速度往往不尽人意，可以考虑使用随机梯度下降法来解决收敛速度的问题。但上面两种在最小值附近，都存在以一种曲折的慢速逼近方式来逼近最小点的问题。所以在LR回归的实际算法中，用到的是牛顿法，拟牛顿法（DFP、BFGS、L-BFGS）。

由于求解最优解的问题，其实是一个凸优化的问题，这些数值优化方法的区别仅仅在于选择什么方向走向最优解，而这个方向通常是优化函数在当前点的一阶导数（梯度）或者二阶导数（海森Hessian矩阵）决定的。比如梯度下降法用的就是一阶导数，而牛顿法和拟牛顿法用的就是二阶导数。

带惩罚项的LR回归

L2惩罚的LR回归：

$\min_w \{\sum_{n=1}^N\{t_nlny_n+(1-t_n)ln(1-y_n)\} + \frac{\lambda}{2}w^Tw\}$

上式中， $\lambda$ 是用于调节目标函数和惩罚项之间关系的， $\lambda$ 越大，惩罚力度越大，所得到的 $w$ 的最优解越趋近于0，或者说参数向量越稀疏； $\lambda$ 越小，惩罚力度越小，模型越复杂，也越能体现训练集的数据特征。

L1惩罚的LR回归:

$\min_w \{\sum_{n=1}^N\{t_nlny_n+(1-t_n)ln(1-y_n)\} + {\lambda \over 2}\left|| w \right ||_1\}$

$||w||_1$ 为1范数，即所有元素的绝对值之和。

L1惩罚项可用于特征选择，会使模型的特征变得稀疏。

为什么逻辑回归比线性回归要好？

虽然逻辑回归能够用于分类，不过其本质还是线性回归。它仅在线性回归的基础上，在特征到结果的映射中加入了一层sigmoid函数（非线性）映射，即先把特征线性求和，然后使用sigmoid函数来预测。然而，正是这个简单的逻辑函数，使得逻辑回归模型成为了机器学习领域一颗耀眼的明星。

这主要是由于线性回归在整个实数域内敏感度一致，而分类范围，只需要在[0,1]之内。而逻辑回归就是一种减小预测范围，将预测值限定为[0,1]间的一种回归模型。逻辑曲线在z=0时，十分敏感，在z>>0或z<<0处，都不敏感，将预测值限定为[0,1]。

从梯度更新视角来看，为什么线性回归在整个实数域内敏感度一致不好。

线性回归和LR的梯度更新公式是一样的,如下：

$\theta_j :={1\over m} \alpha(h_\theta(x^{(i)})-y^{(i)}) x^{(i)}_j$

唯一不同的是假设函数 $h_\theta(x^{(i)})$ ， $y\in \{0,1\}$ ，对于LR而言， $h_\theta(x^{(i)})\in [0,1]$ ，那么梯度更新的幅度就不会太大。而线性回归 $h_\theta(x^{(i)})$ 在整个实数域上，即使已经分类正确的点，在梯度更新的过程中也会大大影响到其它数据的分类，就比如有一个正样本，其输出为10000，此时梯度更新的时候，这个样本就会大大影响负样本的分类。而对于LR而言，这种非常肯定的正样本并不会影响负样本的分类情况！

参考文章：

Logistic Regression 的前世今生（理论篇）