给一个正整数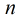
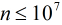
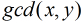
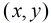
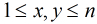
其实挺难看出这题要用欧拉定理做的。
欧拉函数φ:φ(n)表示1 … n中与n互质的整数个数。即:
for(int i=1;i<=n;++i)
if(gcd(i,n)==1)
s++;
(先考虑x<y的,最后*2)所以说,如果这道题目改成:求使得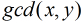
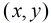
那么怎么把原题和欧拉函数联系起来?
可以发现,若gcd(x,y)=1,那么gcd(x*质数,y*质数)=质数。反过来若gcd(x,y)=质数,那么x,y都能被该质数整除。所以不如枚举[gcd(x,y)=质数]的这个质数,此时gcd(x/质数,y/质数)=1,就又变成欧拉函数了,范围从原来y∈[1,n]变成y/质数∈[1,n/质数]。可以用一个前缀和f[i]一步求。
——————————————————————————————————————————————————————————
分析:对于本题,因为是使得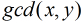
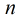
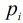
需要求在区间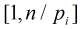
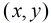
也就是说,现在问题转化为:在区间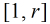
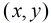
是有序对,不妨设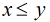
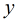
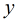
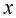
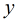
我们可以递推法求欧拉函数,将得到的答案乘以2即可,但是这里乘以2后还有漏计算了的,那么有哪些呢?
是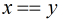
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <bitset>
using namespace std;
typedef long long LL;
const int N=10000010;
bitset<N> prime;
LL phi[N];
LL f[N];
int p[N];
int k;
void isprime() {
k=0;
prime.set();
for(int i=2;i<N;i++) {
if(prime[i]) {
p[k++]=i;
for(int j=i+i;j<N;j+=i)
prime[j]=false;
}
}
}
void Oula() {
for(int i=1;i<N;i++) phi[i]=i;
for(int i=2;i<N;i+=2)phi[i] >>= 1;
for(int i=3;i<N;i+=2) {
if(phi[i]==i) {
for(int j=i;j<N;j+=i)
phi[j]=phi[j]-phi[j]/i;
}
}
f[1]=0;
for(int i=2;i<N;i++)
f[i]=f[i-1]+(phi[i]<<1); //前i个数的欧拉值前缀和
}
LL Solve(int n) {
LL ans=0;
for(int i=0;i<k&&p[i]<=n;i++)//枚举质数p[i]
ans+=f[n/p[i]]+1; //+1是把x=y=p[i]时算上
return ans;
}
int main() {
Oula();
isprime();
int n;
scanf("%d",&n);
printf("%I64d\n",Solve(n));
return 0;
}