基于嵌入莱维飞行的灰狼优化(LGWO)算法的函数寻优算法

一、理论基础

1、灰狼优化算法

受狼群猎食行为的启发，Mirjalili等提出了灰狼优化算法(Grey Wolf Optimization，GWO)，该算法由于控制参数较少，因此实现方便。灰狼优化算法模拟灰狼的社会等级制度和猎食行为，视灰狼为猎食者顶端，即处于食物链最上层。GWO算法建立了一个模型：狼群中每一个灰狼代表了种群的一个潜在解，其中领导狼群的$\alpha$狼位置是最好的解，处于狼群等级第二阶层的$\beta$狼位置和负责侦察、警戒、打围以及看守的$\delta$狼位置分别为优解和次优解，其他的候选解是阶层较低的$\omega$狼位置。GWO算法包括如下三个步骤。

（1）种群初始化

由于GWO的性能受种群初始值影响较小，因此在该算法中采用随机产生种群的方法，即：$$X_{i,j}\sim U(l{b}_j,u{b}_j)\text{\hspace{1em}(1)}$$其中，$X$为灰狼种群， i ∈ { 1 , 2 , 3 … , N } i∈\{1,2,3…,N\} i∈{ 1,2,3…,N}且 j ∈ { 1 , 2 , 3 … , s i z e p o p } j∈\{1,2,3…, sizepop\} j∈{ 1,2,3…,sizepop}，$N$是灰狼种群个数，$sizepop$是种群维数；$lb$和$ub$分别为搜索区间的下界和上界；$Ｕ$是随机均匀分布函数。

（2）种群搜索

通过公式(2)和公式(3)搜索接近猎物：$$\overrightarrow{\mathbf{D}}=|\overrightarrow{\mathbf{C}}\cdot {\overrightarrow{\mathbf{X}}}_p(\mathbf{t})-\overrightarrow{\mathbf{X}}(\mathbf{t})|\text{\hspace{1em}(2)}$$$$\overrightarrow{\mathbf{X}}(t+1)={\overrightarrow{\mathbf{X}}}_p(t)-\overrightarrow{\mathbf{A}}\cdot \overrightarrow{\mathbf{D}}\text{\hspace{1em}(3)}$$其中，$\overrightarrow{\mathbf{D}}$为猎物与灰狼之间的距离；$t$为迭代的次数；$\overrightarrow{\mathbf{C}}$和$\overrightarrow{\mathbf{A}}$为系数向量；$\overrightarrow{\mathbf{X}}$和${\overrightarrow{\mathbf{X}}}_p$为灰狼位置向量和猎物位置向量。
向量$\overrightarrow{\mathbf{A}}$和$\overrightarrow{\mathbf{C}}$的计算公式如下：$$\overrightarrow{\mathbf{A}}=2\cdot \overrightarrow{\mathbf{a}}\cdot \overrightarrow{{\mathbf{r}}_1}-\overrightarrow{\mathbf{a}}\text{\hspace{1em}(4)}$$$$\overrightarrow{\mathbf{C}}=2\cdot \overrightarrow{{\mathbf{r}}_2}\text{\hspace{1em}(5)}$$其中，$r_1$和$r_2$是在$[0,1]$范围内的随机数。一般情况，$\overrightarrow{\mathbf{a}}$控制参数在$[0,2]$范围内取值，且随着算法迭代次数的增加而线性递减。对应于公式(3)，$|\overrightarrow{\mathbf{A}}|\ge 1$意味着灰狼进行全局搜索， $|\overrightarrow{\mathbf{A}}|＜1$表示灰狼进行局部搜索。

（3）种群位置更新

通过计算灰狼优化算法的目标函数值，得到最优解、优解和次优解设置为$\alpha$狼、$\beta$狼和$\delta$狼，其他灰狼的位置由$\alpha$狼、$\beta$狼和$\delta$狼的位置共同决定，如公式(6)~公式(8)所示。在产生新群体后，对种群中的元素进行边界控制，完成一次迭代。重复上述过程，直到满足算法终止条件，最后输出最优解。$$\{\begin{array}{l}{\overrightarrow{\mathbf{D}}}_{\alpha }=|{\overrightarrow{\mathbf{C}}}_1\cdot {\overrightarrow{\mathbf{X}}}_{\alpha }-\overrightarrow{\mathbf{X}}|\\ {\overrightarrow{\mathbf{D}}}_{\beta }=|{\overrightarrow{\mathbf{C}}}_2\cdot {\overrightarrow{\mathbf{X}}}_{\beta }-\overrightarrow{\mathbf{X}}|\\ {\overrightarrow{\mathbf{D}}}_{\delta }=|{\overrightarrow{\mathbf{C}}}_3\cdot {\overrightarrow{\mathbf{X}}}_{\delta }-\overrightarrow{\mathbf{X}}|\end{array}\text{\hspace{1em}(6)}$$$$\{\begin{array}{l}{\overrightarrow{\mathbf{X}}}_1={\overrightarrow{\mathbf{X}}}_{\alpha }-{\overrightarrow{\mathbf{A}}}_1\cdot {\overrightarrow{\mathbf{D}}}_{\alpha }\\ {\overrightarrow{\mathbf{X}}}_2={\overrightarrow{\mathbf{X}}}_{\beta }-{\overrightarrow{\mathbf{A}}}_2\cdot {\overrightarrow{\mathbf{D}}}_{\beta }\\ {\overrightarrow{\mathbf{X}}}_3={\overrightarrow{\mathbf{X}}}_{\delta }-{\overrightarrow{\mathbf{A}}}_3\cdot {\overrightarrow{\mathbf{D}}}_{\delta }\end{array}\text{\hspace{1em}(7)}$$$$\overrightarrow{\mathbf{X}}(t+1)=\frac{{\overrightarrow{\mathbf{X}}}_1+{\overrightarrow{\mathbf{X}}}_2+{\overrightarrow{\mathbf{X}}}_3}{3}\text{\hspace{1em}(8)}$$

2、莱维飞行

“莱维飞行”以法国数学家保罗·莱维命名，指的是步长的概率分布为重尾分布的随机行走，也就是说在随机行走的过程中有相对较高的概率出现大跨步。莱维飞行的名称来源于本华·曼德博（Benoît Mandelbrot，莱维的学生）。他用“柯西飞行”来指代步长分布是柯西分布的随机行走，用“瑞利飞行”指代步长分布是正态分布（尽管正态分布没有重尾）的随机行走（瑞利分布是二维独立同方差正态变量模长的分布）。后来学者还进一步将莱维飞行的概念从连续空间推广到分立格点上的随机运动。图1是莱维飞行轨迹示意图：

图1 莱维飞行轨迹示意图

3、嵌入莱维飞行的灰狼优化算法

灰狼优化（Gray Wolf Optimization , GWO）算法具有不过分依赖参数设置和方便实现等优点，但GWO算法在解决复杂优化问题时仍然容易过早陷入局部极值，即出现早熟收敛的现象。为解决上述问题，Heidari提出了LGWO算法。LGWO算法对于GWO算法主要进行了三个方面的改进：

1. $\delta$狼在种群中的作用被其他狼代替，即LGWO算法中只包括$\alpha$狼，$\beta$狼和$\omega$狼；
2. 通过莱维飞行改进GWO算法；
3. 将贪婪搜索策略应用到经莱维飞行改进的GWO算法中。

LGWO算法的具体过程总结如下，描述如下：
（1）种群初始化，其过程同GWO算法一致。
（2）种群搜索，其过程同GWO算法一致。
（3）通过计算LGWO算法的目标函数值，得到最优解$\alpha$狼、优解$\beta$狼，其他灰狼的位置由$\alpha$狼和$\beta$狼的位置共同决定，如公式(9)所示：$$\overrightarrow{\mathbf{X}}(t+1)=\{\begin{array}{l}0.5\times \left({\overrightarrow{\mathbf{X}}}_{\alpha }-{\overrightarrow{\mathbf{A}}}_1{\overrightarrow{\mathbf{D}}}_{\alpha }+{\overrightarrow{\mathbf{X}}}_{\beta }-{\overrightarrow{\mathbf{A}}}_2{\overrightarrow{\mathbf{D}}}_{\beta }\right)+\alpha \oplus Levi(\beta )|\mathbf{A}|\ge 0.5\\ 0.5\times \left({\overrightarrow{\mathbf{X}}}_{\alpha }-{\overrightarrow{\mathbf{A}}}_1{\overrightarrow{\mathbf{D}}}_{\alpha }+{\overrightarrow{\mathbf{X}}}_{\beta }-{\overrightarrow{\mathbf{A}}}_2{\overrightarrow{\mathbf{D}}}_{\beta }\right)|\mathbf{A}|<0.5\end{array}\text{\hspace{1em}(9)}$$其中，$$\alpha \oplus Levi(\beta )\sim 0.01\frac{u}{|v{|}^{-\beta }}(\overrightarrow{\mathbf{X}}(t)-{\overrightarrow{\mathbf{X}}}_{\alpha }(t))\text{\hspace{1em}(10)}$$其中，$u$和$v$服从正态分布：$$u\sim N(0,{\sigma }_u^2),v\sim N(0,{\sigma }_v^2)\text{\hspace{1em}(11)}$$$${\sigma }_u={\left[\frac{\Gamma (1+\beta )sin(\frac{\pi \beta }{2})}{\Gamma (\frac{1+\beta }{2})\beta \times 2^{\frac{\beta -1}{2}}}\right]}^{\frac{1}{\beta }},{\sigma }_v=1\text{\hspace{1em}(12)}$$在Heidari提出的LGWO算法中，参数$\beta$是$[0,2]$的随机数。
在保留前一代解，通过公式(9)产生新群体后记为${\overrightarrow{\mathbf{X}}}_{new}(t)$，通过贪婪选择策略公式(13)进行选择判断是否保留更新后的灰狼，完成一次迭代。重复上述过程，直到满足算法终止条件，最后输出最优解。$$\overrightarrow{\mathbf{X}}(t+1)=\{\begin{array}{l}\overrightarrow{\mathbf{X}}(t),f({\overrightarrow{\mathbf{X}}}_{new}(t))>f(\overrightarrow{\mathbf{X}}(t))and{r}_{new}<p\\ {\overrightarrow{\mathbf{X}}}_{new}(t),otherwise\end{array}\text{\hspace{1em}(13)}$$贪婪选择(GS)策略中使用“适者生存”的概念，通过用概率$p$体现。根据这一策略，新的一次迭代中位置更优的狼可以使种群更加丰富，而新的一次迭代中位置更糟的狼则被忽视。其中$r_{new}$和$p$是$[0,1]$的随机数。通过应用贪婪选择策略，LGWO算法有更好的随机性。同时应用贪婪选择使每次迭代获得的更优位置的狼得以保留，因此LGWO算法拥有更强的搜索能力。

二、MATLAB程序实现

1、初始化参数

%% 清空环境变量
clear all 
clc

%% 初始化参数
N = 30;   % 种群个数
Function_name = 'F10';   % 从F1到F23的测试函数的名称（本文中的表1、2、3）
Max_iteration = 500;     % 最大迭代次数

2、LGWO

function [Alpha_score, Alpha_pos, Convergence_curve] = LGWO(N, Max_iter, lb, ub, dim, fobj)
%% 嵌入莱维飞行的灰狼优化算法
% 初始化alpha, beta和delta_pos
Alpha_pos = zeros(1, dim);
Alpha_score = inf;  % 将此更改为-inf以解决最大化问题
Beta_pos = zeros(1,dim);
Beta_score = inf;   % 将此更改为-inf以解决最大化问题
% 初始化种群位置
Positions = initialization(N, dim, ub, lb);
Convergence_curve = zeros(1, Max_iter);  % 收敛曲线
l = 0;    % 循环计数器
% 主要循环
while l < Max_iter
    l
    for i = 1:size(Positions, 1)
        % 边界处理
        Flag4ub = Positions(i, :)>ub;
        Flag4lb = Positions(i, :)<lb;
        Positions(i, :) = (Positions(i, :).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
%         Positions(i, :) = max(Positions(i, :), lb);
%         Positions(i, :) = min(Positions(i, :), ub);
        % 计算每个种群的目标函数
        fitness = fobj(Positions(i, :));
        % 更新Alpha, Beta和Delta
        if fitness < Alpha_score
            Alpha_score = fitness;        % 更新alpha
            Alpha_pos = Positions(i, :);
        elseif fitness < Beta_score
            Beta_score = fitness;           % 更新beta
            Beta_pos = Positions(i, :);
        end
    end
    a = 2-l*((2)/Max_iter);      % a从2线性减小到0    
    % 更新包括omegas在内的种群的位置
    for i = 1:size(Positions, 1)
        for j = 1:size(Positions, 2)
            r1 = rand();             % r1是[0,1]中的随机数
            r2 = rand();             % r2是[0,1]中的随机数
            A1 = 2*a*r1-a;        % 公式（4）
            C1 = 2*r2;            % 公式（5）
            D_alpha = abs(C1*Alpha_pos(j)-Positions(i, j));  % 公式（6）-第一部分
%             X1 = Alpha_pos(j)-A1*D_alpha;   % 公式 (7)-第一部分
            
            r1 = rand();
            r2 = rand();
            A2 = 2*a*r1-a;         % 公式（4）
            C2 = 2*r2;             % 公式（5）
            D_beta = abs(C2*Beta_pos(j)-Positions(i, j));   % 公式（6）-第二部分
%             X2 = Beta_pos(j)-A2*D_beta;       % 公式 (7)-第二部分
            
            Positions_old = Positions(i, :);
            A = rand();
            if abs(A) < 0.5
                Positions(i, j) = 0.5*(Alpha_pos(j)-A1*D_alpha+Beta_pos(j)-A2*D_beta);
            else
                beta = 2*rand();
                sigma_u = ((gamma(1+beta)*sin(pi*beta/2))/(gamma((1+beta)/2)*beta*2^(0.5*(beta-1))))^(1/beta);
                u = normrnd(0, sigma_u);
                v = normrnd(0, 1);
                alpha_levi = 0.01*u/abs(v)^(-beta)*(Positions(i, j)-Alpha_pos(j));
                Positions(i, j) = 0.5*(Alpha_pos(j)-A1*D_alpha+Beta_pos(j)-A2*D_beta)+alpha_levi;
            end      
            % 贪婪算法选择
            rnew = rand();
            p = rand();
            if fobj(Positions(i, :)) > fobj(Positions_old) && rnew < p
                Positions(i, :) = Positions_old;
            end 
        end
    end
    l = l+1;
    Convergence_curve(l) = Alpha_score;
end

3、结果显示

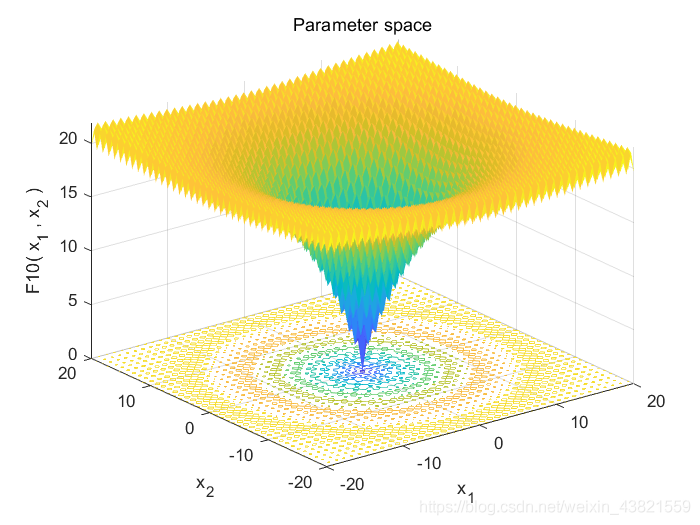
目标函数三维立体图形如图2所示：

图2 目标函数三维立体图形

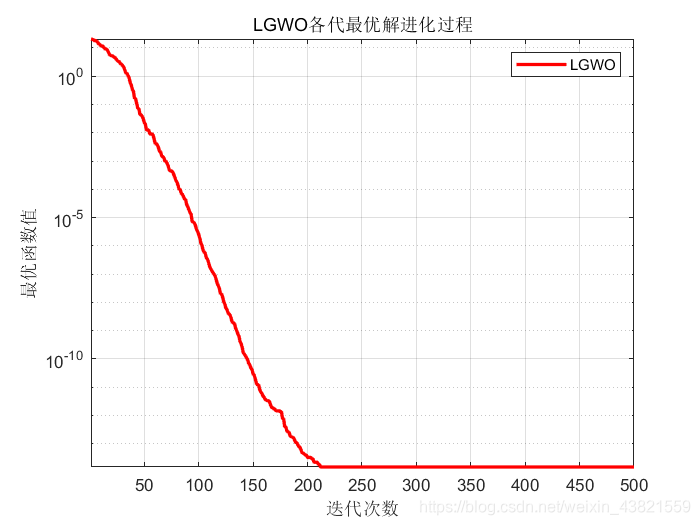
LGWO算法各代最优解进化过程如图3所示：

扫描二维码关注公众号，回复： 13841551 查看本文章

图3 LGWO算法各代最优解进化过程

4、对比分析

LGWO算法和经典GWO算法的最优解进化过程对比图如图4所示：

图4 LGWO算法和经典GWO算法的最优解进化过程对比图

由此可以得出：嵌入莱维飞行的灰狼优化算法比原始灰狼优化算法可以避免陷入局部最优解，并且更快收敛到全局最优。

三、参考文献

[1] Seyedali Mirjalili, Seyed Mohammad Mirjalili, Andrew Lewis. Grey Wolf Optimizer[J]. Advances in Engineering Software, 2014, 69: 46–61.
[2] Ali Asghar Heidari, Parham Pahlavani. An Efficient Modified Grey Wolf Optimizer with Lévy Flight for Optimization Tasks[J]. Applied Soft Computing, 2017, 60: 115-134.
[3] 王世鹏. 无线传感器网络覆盖优化算法研究[D]. 长春: 吉林大学, 2020.