第四章线性系统的根轨迹法
导语
本博文基于自动控制原理(胡寿松第六版)全书,将知识点总结,便于同学们的复习,该篇属于自动控制原理的理论篇,理论性东西较多,阅读起来难免有点枯燥,但既然坚持了,那就把它读完吧,因作者也是在复习考研,也是刚毕业的大学生,总结的东西难免会有所纰漏,如发现,请在评论区提醒,望共同进步,考研成功上岸!
4.1 根轨迹法的基本概念
- 根轨迹概念
根轨迹是指开环系统某一参数从零变化到无穷时,闭环系统特征方程式的根在 s s s平面上变化的轨迹。 - 根轨迹与系统性能
实例1:设控制系统如下图(a)所示,其闭环传递函数为:
Φ ( s ) = C ( s ) R ( s ) = 2 K s 2 + 2 s + 2 K \Phi(s)=\frac{C(s)}{R(s)}=\frac{2K}{s^2+2s+2K} Φ(s)=R(s)C(s)=s2+2s+2K2K
特征方程为:
s 2 + 2 s + 2 K = 0 s^2+2s+2K=0 s2+2s+2K=0
特征根为:
s 1 = − 1 + 1 − 2 K , s 2 = − 1 − 1 − 2 K s_1=-1+\sqrt{1-2K},s_2=-1-\sqrt{1-2K} s1=−1+1−2K,s2=−1−1−2K
上述系统的根轨迹如下图所示:
根轨迹图的说明:如图红色实线就是系统的根轨迹,根轨迹上的箭头表示随着K值的增大,根轨迹的变化趋势,标注的数值代表与闭环极点位置相对应的开环增益K的数值。
用上根轨迹图来说明根轨迹和系统性能的联系:
a.稳定性
根轨迹全部在s左半平面,系统对所有K值都是稳定的;当根轨迹越过虚轴进入s右半平面,此时根轨迹与虚轴交点处的K值,就是临界开环增益。
b.稳态性能
如果给定系统的稳态误差要求,由根轨迹图可以确定闭环极点位置的容许范围,在一般情况下,根轨迹图上标注的参数不是开环增益,而是根轨迹增益,两者仅相差一个常数,可以进行换算。
c.动态性能
分 析 实 例 中 的 根 轨 迹 , 当 0 < K < 0.5 时 , 所 有 闭 环 极 点 位 于 实 轴 上 , 系 统 为 过 阻 尼 系 统 , 单 位 阶 跃 响 应 为 非 周 期 过 程 ; 当 K = 0.5 时 , 闭 环 两 个 实 数 极 点 重 合 , 系 统 为 临 界 阻 尼 系 统 , 单 位 阶 跃 响 应 仍 为 非 周 期 过 程 , 但 响 应 速 度 叫 0 < K < 0.5 情 况 为 快 ; 当 K > 0.5 时 , 闭 环 极 点 为 复 数 极 点 , 系 统 为 欠 阻 尼 系 统 , 单 位 阶 跃 响 应 为 阻 尼 振 荡 过 程 , 且 超 调 量 随 着 K 值 的 增 大 而 增 大 , 但 调 节 时 间 的 变 化 不 显 著 。 分析实例中的根轨迹,当0<K<0.5时,所有闭环极点位于实轴上,系统为过阻尼系统,单位阶跃响应为非周期过程;当K=0.5时,闭环两个实数极点重合,系统为临界阻尼系统,单位阶跃响应仍为非周期过程,但响应速度叫0<K<0.5情况为快;当K>0.5时,闭环极点为复数极点,系统为欠阻尼系统,单位阶跃响应为阻尼振荡过程,且超调量随着K值的增大而增大,但调节时间的变化不显著。 分析实例中的根轨迹,当0<K<0.5时,所有闭环极点位于实轴上,系统为过阻尼系统,单位阶跃响应为非周期过程;当K=0.5时,闭环两个实数极点重合,系统为临界阻尼系统,单位阶跃响应仍为非周期过程,但响应速度叫0<K<0.5情况为快;当K>0.5时,闭环极点为复数极点,系统为欠阻尼系统,单位阶跃响应为阻尼振荡过程,且超调量随着K值的增大而增大,但调节时间的变化不显著。 - 闭环零、极点与开环零、极点之间的关系
设控制系统如下图(b)所示,其闭环传递函数为:
Φ ( s ) = G ( s ) 1 + G ( s ) H ( s ) \Phi(s)=\frac{G(s)}{1+G(s)H(s)} Φ(s)=1+G(s)H(s)G(s)
一般情况下,前向通路传递函数 G ( s ) G(s) G(s)可表示为:
G ( s ) = K G ( τ 1 s + 1 ) ( τ 2 2 s 2 + 2 ζ 1 τ 2 s + 1 ) … s ν ( T 1 s + 1 ) ( T 2 2 s 2 + 2 ζ 2 T 2 s + 1 ) … = K G ∗ ∏ i = 1 f ( s − z i ) ∏ i = 1 q ( s − p i ) G(s)=\frac{K_G(\tau_1s+1)(\tau_2^2s^2+2\zeta_1\tau_2s+1)\dots}{s^{\nu}(T_1s+1)(T_2^2s^2+2\zeta_2T_2s+1)\dots}=K_G^*\frac{\prod_{i=1}^f (s-z_i)}{\prod_{i=1}^q (s-p_i)} G(s)=sν(T1s+1)(T22s2+2ζ2T2s+1)…KG(τ1s+1)(τ22s2+2ζ1τ2s+1)…=KG∗∏i=1q(s−pi)∏i=1f(s−zi)
式 中 : K G 为 前 向 通 路 增 益 ; K G ∗ 为 前 向 通 路 根 轨 迹 增 益 。 式中:K_G为前向通路增益;K_G^*为前向通路根轨迹增益。 式中:KG为前向通路增益;KG∗为前向通路根轨迹增益。
反馈通路传递函数 H ( s ) H(s) H(s)可表示为:
H ( s ) = K H ∗ ∏ j = 1 l ( s − z j ) ∏ j = 1 h ( s − p j ) H(s)=K_H^*\frac{\prod_{j=1}^l (s-z_j)}{\prod_{j=1}^h (s-p_j)} H(s)=KH∗∏j=1h(s−pj)∏j=1l(s−zj)
则开环传递函数为:
G ( s ) H ( s ) = K ∗ ∏ i = 1 f ( s − z i ) ∏ j = 1 l ( s − z j ) ∏ i = 1 q ( s − p i ) ∏ j = 1 h ( s − p j ) G(s)H(s)=K^*\frac{\prod_{i=1}^f (s-z_i)\prod_{j=1}^l (s-z_j)}{\prod_{i=1}^q (s-p_i)\prod_{j=1}^h (s-p_j)} G(s)H(s)=K∗∏i=1q(s−pi)∏j=1h(s−pj)∏i=1f(s−zi)∏j=1l(s−zj)
式 中 : K ∗ = K G ∗ K H ∗ 称 为 开 环 系 统 根 轨 迹 增 益 式中:K^*=K_G^*K_H^*称为开环系统根轨迹增益 式中:K∗=KG∗KH∗称为开环系统根轨迹增益。
则闭环传递函数为:
Φ ( s ) = K G ∗ ∏ i = 1 f ( s − z i ) ∏ j = 1 h ( s − p j ) ∏ i = 1 n ( s − p i ) + K ∗ ∏ j = 1 m ( s − z j ) \Phi(s)=\frac{K_G^*\prod_{i=1}^f (s-z_i)\prod_{j=1}^h (s-p_j)}{\prod_{i=1}^n (s-p_i)+K*\prod_{j=1}^m (s-z_j)} Φ(s)=∏i=1n(s−pi)+K∗∏j=1m(s−zj)KG∗∏i=1f(s−zi)∏j=1h(s−pj)
式 中 : f + l = m , q + h = n 式中:f+l=m,q+h=n 式中:f+l=m,q+h=n。
结论:
a.闭环系统根轨迹增益,等于开环系统前向通路根轨迹增益;
b.闭环零点由开环前向通路传递函数的零点和反馈通路传递函数极点组成;
c.闭环极点和开环零点、开环极点以及根轨迹增益 K ∗ K* K∗均有关。 - 根轨迹方程
根轨迹是系统所有闭环极点的集合。
闭环特征方程为:
1 + G ( s ) H ( s ) = 0 1+G(s)H(s)=0 1+G(s)H(s)=0
当系统有 m m m个开环零点和 n n n个开环极点时,可以得到如下式子:
K ∗ ∏ j = 1 m ( s − z j ) ∏ i = 1 n ( s − p i ) = − 1 K^*\frac{\prod_{j=1}^m (s-z_j)}{\prod_{i=1}^n (s-p_i)}=-1 K∗∏i=1n(s−pi)∏j=1m(s−zj)=−1
式 中 : z j 为 已 知 的 开 环 零 点 ; p i 为 已 知 的 开 环 极 点 ; K ∗ 从 零 变 化 到 无 穷 。 上 式 称 为 根 轨 迹 方 程 。 式中:z_j为已知的开环零点;p_i为已知的开环极点;K^*从零变化到无穷。上式称为根轨迹方程。 式中:zj为已知的开环零点;pi为已知的开环极点;K∗从零变化到无穷。上式称为根轨迹方程。
根轨迹可以由如下两个方程描述,第一个方程称为相角条件,第二个方程称为模值条件。
∑ j = 1 m ∠ ( s − z j ) − ∑ i = 1 n ∠ ( s − p i ) = ( 2 k + 1 ) π ( k = 0 , ± 1 , ± 2 , … ) \sum_{j=1}^m \angle(s-z_j)-\sum_{i=1}^n \angle(s-p_i)=(2k+1)\pi(k=0,±1,±2,\dots) j=1∑m∠(s−zj)−i=1∑n∠(s−pi)=(2k+1)π(k=0,±1,±2,…)
K ∗ = ∏ i = 1 n ∣ s − p i ∣ ∏ j = 1 m ∣ s − z j ∣ K^*=\frac{\prod_{i=1}^n |s-p_i|}{\prod_{j=1}^m |s-z_j|} K∗=∏j=1m∣s−zj∣∏i=1n∣s−pi∣
其中:相角条件是确定s平面上根轨迹的充分必要条件,模值条件用于确定根轨迹上各点的 K ∗ K^* K∗值。
4.2 根轨迹绘制的基本法则
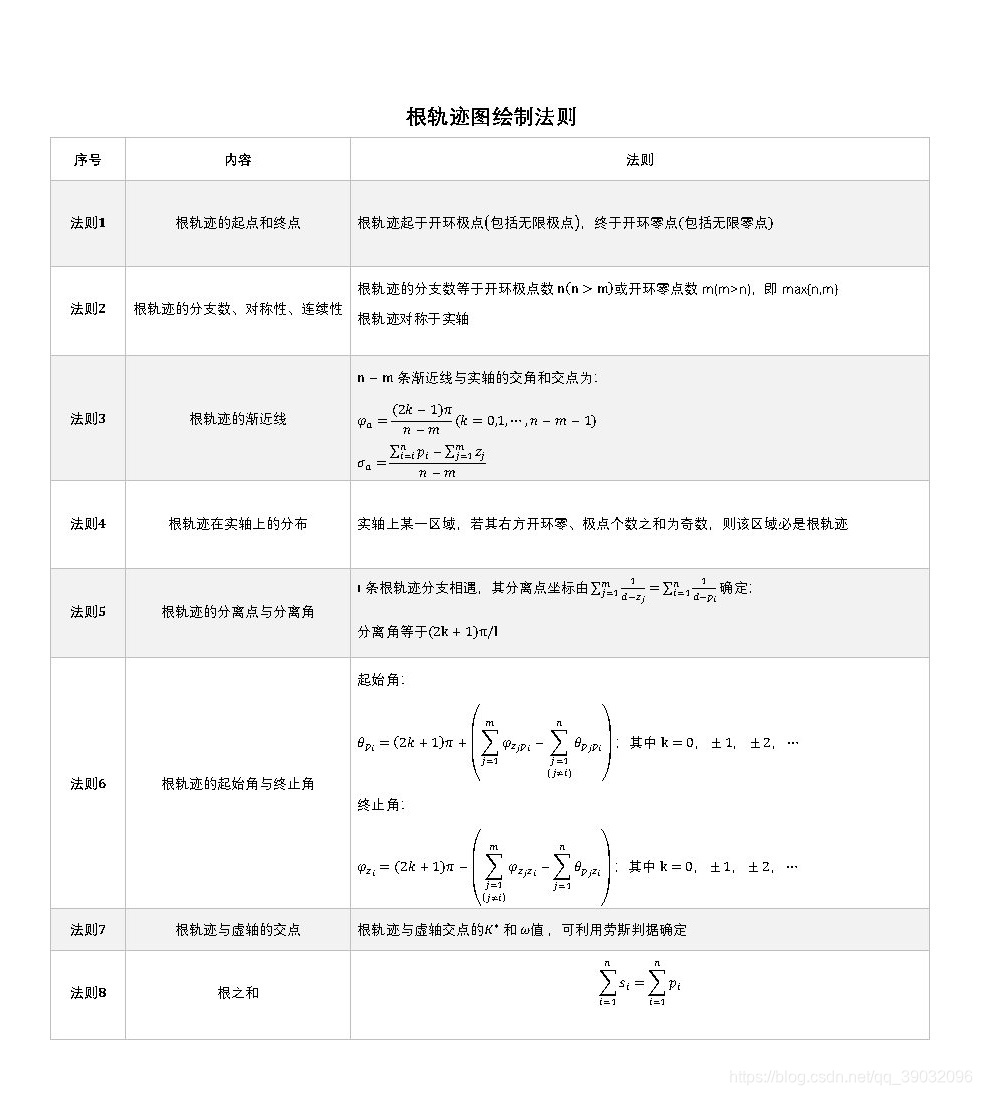
根轨迹绘制法则可参考链接: 自动控制–控制系统根轨迹篇.在控制系统根轨迹篇详细介绍了180°根轨迹和0°根轨迹的绘制法则,并且具有例题进行说明。
4.3 广义根轨迹
- 参数根轨迹
定义:以非开环增益为可变参数绘制的根轨迹称为参数根轨迹。
绘制的步骤如下:
a.由特征方程导出根轨迹方程的标准形式:
等效开环传递函数 Φ 等 效 ( s ) = − 1 \Phi_{等效}(s)=-1 Φ等效(s)=−1
D ( s ) = 1 + G ( s ) H ( s ) = 0 ⇒ 1 + 参 数 N ( s ) M ( s ) = 0 ⇒ 参 数 N ( s ) M ( s ) = − 1 D(s)=1+G(s)H(s)=0\Rightarrow1+参数\frac{N(s)}{M(s)}=0\Rightarrow参数\frac{N(s)}{M(s)}=-1 D(s)=1+G(s)H(s)=0⇒1+参数M(s)N(s)=0⇒参数M(s)N(s)=−1
b.根轨迹绘制方法绘制根轨迹
c.通用根轨迹分析法分析 - 零度根轨迹
a.零度根轨迹产生的原因
①包含正反馈回路: D ( s ) = 1 − G ( s ) H ( s ) = 0 ⇒ G ( s ) H ( s ) = 1 D(s)=1-G(s)H(s)=0\Rightarrow{G(s)H(s)=1} D(s)=1−G(s)H(s)=0⇒G(s)H(s)=1;
②系统中含有 s s s最高次的系数为负的因子,例如:
G ( s ) H ( s ) = k ( 1 − 0.5 s ) s ( 0.2 s + 1 ) = − 1 ⇒ k ( 0.5 s − 1 ) s ( 0.2 s + 1 ) = 1 G(s)H(s)=\frac{k(1-0.5s)}{s(0.2s+1)}=-1\Rightarrow\frac{k(0.5s-1)}{s(0.2s+1)}=1 G(s)H(s)=s(0.2s+1)k(1−0.5s)=−1⇒s(0.2s+1)k(0.5s−1)=1
③ k k k的取值范围 − ∞ → 0 -\infty\rightarrow0 −∞→0
b.零度根轨迹绘制法则
零度根轨迹绘制法则可参考链接: 自动控制–控制系统根轨迹篇.在控制系统根轨迹篇详细介绍了180°根轨迹和0°根轨迹的绘制法则,并且具有例题进行说明。
4.4 系统性能的分析
- 闭环零极点与时间响应
a.在工程实践中,常采用主导极点对高阶系统进行近似分析;
b.主导极点定义为对整个时间响应过程起主要作用的闭环极点;
c.只有既接近虚轴,又不十分接近闭环零点的闭环极点,才可能称为主导极点;
d.如果闭环零、极点相距很近,这样的闭环零、极点称为偶极子;只要偶极子不十分接近坐标原点,它们对系统动态性能的影响甚微,从而可以忽略它们的存在;
e.如果闭环零、极点之间的距离比它们本身的模值小一个数量级,则这一对闭环零、极点就构成偶极子。 - 系统性能的定性分析
闭环系统零、极点位置对时间响应性能的影响,归纳为以下几点:
a.稳定性。如果闭环极点全部位于s左半平面,则系统一定是稳定的,即稳定性只与闭环极点位置有关,与闭环零点的位置无关;
b.运动形式。如果闭环系统无零点,且闭环极点均为实数极点,则时间响应一定是单调的,如果闭环极点均为复数极点,则时间响应一般是振荡的;
c.超调量。超调量主要取决于闭环复数主导极点的衰减率 σ 1 / ω d = ζ / 1 − ζ 2 \sigma_1/\omega_d=\zeta/\sqrt{1-\zeta^2} σ1/ωd=ζ/1−ζ2,并与其他闭环零、极点接近坐标原点的程度有关;
d.调节时间。调节时间主要取决于最靠近虚轴的闭环复数极点的实部绝对值 σ 1 = ζ ω n \sigma_1=\zeta\omega_n σ1=ζωn;如果实数极点距虚轴最近,且它附近没有实数零点,则调节时间主要取决于该实数极点的模值;
e.实数零、极点影响。零点减小系统阻尼,使峰值时间提前,超调量增大;极点增大系统阻尼,使峰值时间滞后,超调量减小;
f.偶极子及其处理。如果零、极点之间的距离比它们本身的模值小一个数量级,则它们就构成偶极子。远离原点的偶极子,其影响可以忽略,接近原点的偶极子,需要考虑其影响;
g.主导极点。在s平面上,最靠近虚轴而附近又无闭环零点的一些闭环极点,对系统性能影响最大,称为主导极点,凡比主导极点的实部大3~6倍以上的其他闭环零、极点,其影响可以忽略。
4.5 控制系统复域设计
实例分析:自动焊接头控制
题目:自动焊接头需要进行精确定位控制,其控制系统结构图如下图(a)所示,图中, K 1 K_1 K1为放大器增益, K 2 K_2 K2为测速反馈系数。
设计要求:用根轨迹法选择参数 K 1 K_1 K1与 K 2 K_2 K2,使系统满足如下性能指标:
a.系统对斜坡输入响应的稳态误差≤斜坡幅值的35%;
b.系统主导极点的阻尼比 ζ ≥ 0.707 \zeta≥0.707 ζ≥0.707;
c.系统阶跃响应的调节时间 t s ≤ 3 s ( Δ = 2 % ) t_s≤3s(\Delta=2\%) ts≤3s(Δ=2%)。

解:
由图(a)知,系统开环传递函数为:
G ( s ) = G 1 ( s ) 1 + G 1 ( s ) H 1 ( s ) = K 1 s ( s + 2 + K 1 K 2 ) G(s)=\frac{G_1(s)}{1+G_1(s)H_1(s)}=\frac{K_1}{s(s+2+K_1K_2)} G(s)=1+G1(s)H1(s)G1(s)=s(s+2+K1K2)K1
该系统为Ⅰ型系统,在斜坡输入作用下,存在稳态误差,系统的误差信号:
E ( s ) = R ( s ) 1 + G ( s ) = s ( s + 2 + K 1 K 2 ) s 2 + ( 2 + K 1 K 2 ) s + K 1 R ( s ) E(s)=\frac{R(s)}{1+G(s)}=\frac{s(s+2+K_1K_2)}{s^2+(2+K_1K_2)s+K_1}R(s) E(s)=1+G(s)R(s)=s2+(2+K1K2)s+K1s(s+2+K1K2)R(s)
令 R ( s ) = R / s 2 , 则 稳 态 误 差 为 令R(s)=R/s^2,则稳态误差为 令R(s)=R/s2,则稳态误差为:
e s s ( ∞ ) = lim t → ∞ e ( t ) = lim s → 0 s E ( s ) = 2 + K 1 K 2 K 1 R e_{ss}(\infty)=\lim_{t\to \infty} e(t)=\lim_{s\to0}sE(s)=\frac{2+K_1K_2}{K_1}R ess(∞)=t→∞lime(t)=s→0limsE(s)=K12+K1K2R
根据系统对稳态误差的性能指标要求, K 1 与 K 2 K_1与K_2 K1与K2的选取应满足如下要求:
e s s ( ∞ ) R = 2 + K 1 K 2 K 1 ≤ 0.35 \frac{e_{ss}(\infty)}{R}=\frac{2+K_1K_2}{K_1}≤0.35 Ress(∞)=K12+K1K2≤0.35
上式表明,为了获得较小的稳态误差,应该选择小的 K 2 K_2 K2值。
根据系统对主导极点的阻尼比要求,系统闭环极点应位于s平面上 ζ = 0.707 的 ± 45 ° \zeta=0.707的±45° ζ=0.707的±45°斜线之间;由对系统的调节时间指标要求可知,主导极点实部的绝对值应满足
t s = 4.4 σ ≤ 3 s ( Δ = 2 % ) t_s=\frac{4.4}{\sigma}≤3s(\Delta=2\%) ts=σ4.4≤3s(Δ=2%)
因此有 σ ≥ 1.47 \sigma≥1.47 σ≥1.47。满足设计指标要求的闭环极点,应全部位于图(b)所示的扇形区域内。
设待定参数 α = K 1 , β = K 1 K 2 \alpha=K_1,\beta=K_1K_2 α=K1,β=K1K2,则特征方程为:
D ( s ) = s 2 + ( 2 + K 1 K 2 ) s + K 1 = s 2 + 2 s + β s + α = 0 D(s)=s^2+(2+K_1K_2)s+K_1=s^2+2s+\beta{s}+\alpha=0 D(s)=s2+(2+K1K2)s+K1=s2+2s+βs+α=0
先考虑参数 α = K 1 \alpha=K_1 α=K1的选择。令 β = 0 \beta=0 β=0,则 α \alpha α变换时的根轨迹方程为:
1 + α s ( s + 2 ) = 0 1+\frac{\alpha}{s(s+2)}=0 1+s(s+2)α=0
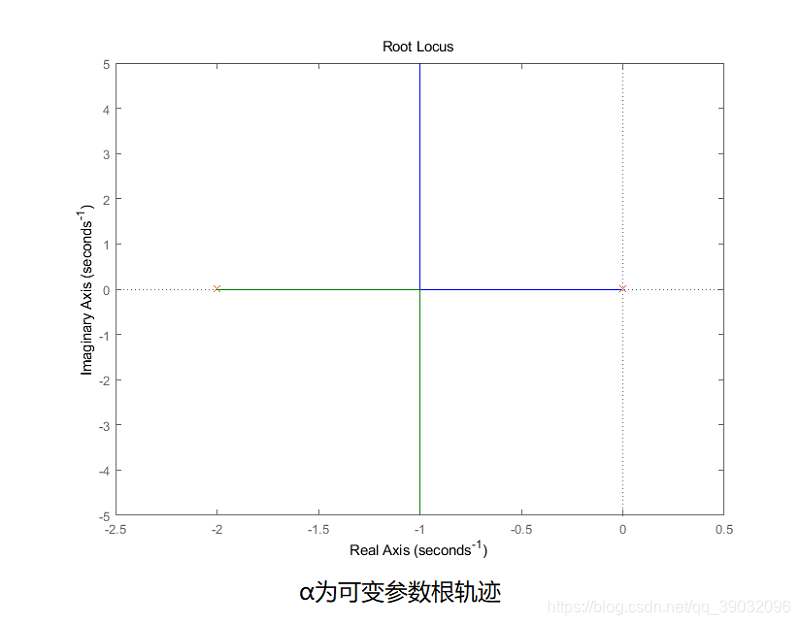
令 α \alpha α从0变化到 ∞ \infty ∞,其根轨迹如图 ( c ) (c) (c)所示,利用模值条件,在图 ( c ) (c) (c)中试取 K 1 = α = 20 K_1=\alpha=20 K1=α=20,其对应的闭环极点为 − 1 ± j 4.36 -1±j4.36 −1±j4.36,参数 β = 20 K 2 \beta=20K_2 β=20K2。
考虑参数 β \beta β的选择。在闭环特征方程 D ( s ) = 0 D(s)=0 D(s)=0中,代入 α = 20 \alpha=20 α=20,则 β \beta β变化时的根轨迹方程为:
1 + β s s 2 + 2 s + 20 = 0 1+\frac{\beta{s}}{s^2+2s+20}=0 1+s2+2s+20βs=0
即
1 + β s ( s + 1 + j 4.36 ) ( s + 1 − j 4.36 ) = 0 1+\beta\frac{s}{(s+1+j4.36)(s+1-j4.36)}=0 1+β(s+1+j4.36)(s+1−j4.36)s=0
令 β \beta β从0变化到 ∞ \infty ∞,其根轨迹图如图 ( d ) (d) (d)所示。
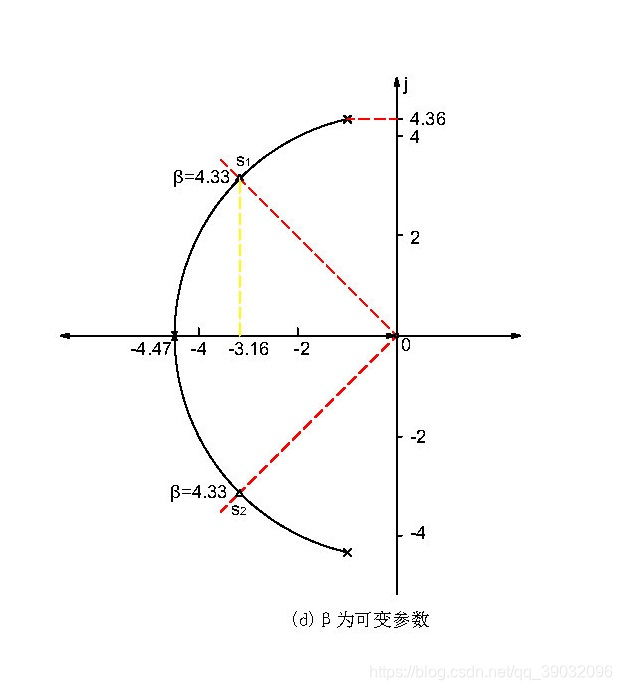
分离点坐标 d = − 4.47 d=-4.47 d=−4.47。当取模值条件 β = 4.33 = 20 K 2 , 即 K 2 = 0.2165 \beta=4.33=20K_2,即K_2=0.2165 β=4.33=20K2,即K2=0.2165时,就得到满足阻尼比 ζ = 0.707 \zeta=0.707 ζ=0.707的闭环主导极点 s 1 , 2 = − 3.16 ± j 3.16 s_{1,2}=-3.16±j3.16 s1,2=−3.16±j3.16,其实部绝对值 σ = 3.16 \sigma=3.16 σ=3.16,调节时间为:
t s = 4.4 σ = 1.39 < 3 ( Δ = 2 % ) t_s=\frac{4.4}{\sigma}=1.39<3(\Delta=2\%) ts=σ4.4=1.39<3(Δ=2%)
相应的稳态误差值:
e s s ( ∞ ) R = 2 + K 1 K 2 K 1 = 2 + β α = 0.3165 < 0.35 \frac{e_{ss}(\infty)}{R}=\frac{2+K_1K_2}{K_1}=\frac{2+\beta}{\alpha}=0.3165<0.35 Ress(∞)=K12+K1K2=α2+β=0.3165<0.35
因而 K 1 = 20 , K 2 = 0.2165 K_1=20,K_2=0.2165 K1=20,K2=0.2165的设计值,满足全部设计指标要求。
M a t l a b 仿 真 结 果 如 下 : Matlab仿真结果如下: Matlab仿真结果如下:
a. M a t l a b 代 码 Matlab代码 Matlab代码
Ga=zpk([],[0 -2],1); %alpha为变参数时的等效开环传递函数模型
figure;rlocus(Ga);alpha=20; %绘制相应系统的根轨迹
hold on;rlocus(Ga,alpha) %求alpha=20时,系统的闭环特征根
Gb=zpk([0],[-1-4.36i -1+4.36i],1) %beta变参数时的等效开环传递函数模型
figure;rlocus(Gb); %绘制相应系统的根轨迹
sgrid(0.707,'new');axis([-8 2 -5 5]) %取阻尼比为0.707
figure;rlocus(Gb);hold on; %绘制相应的根轨迹
beta=4.33;rlocus(Gb,beta) %求beta=4.33时,系统的闭环特征根
K1=20;K2=0.2165;
G1=zpk([],[0 -2],K1);H11=tf([K2 1],[0 1]);
sys=feedback(G1,H11) %系统的闭环传递函数
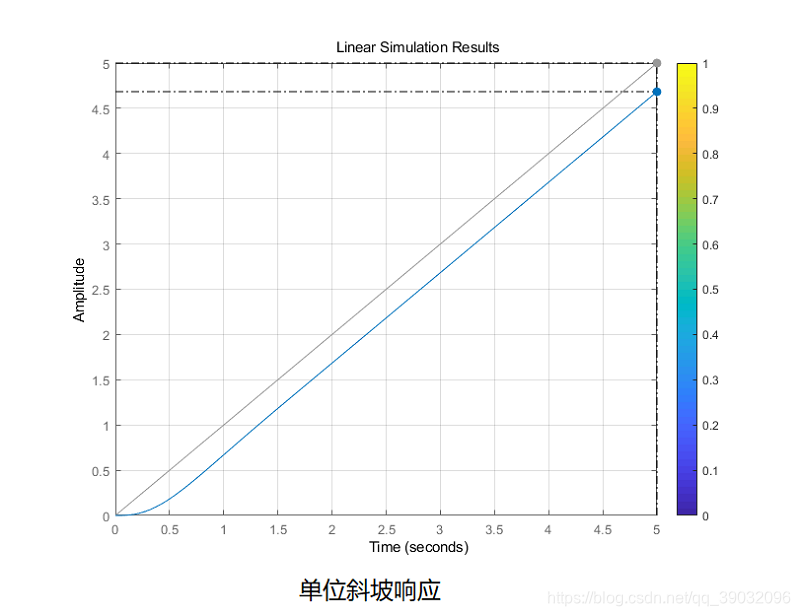
t=0:0.005:5;u=t;
figure;step(sys,t);grid %单位阶跃输入响应
figure;lsim(sys,u,t);grid %单位斜坡输入响应
b.结果