目录标题
Q 代表帮助理解概念的问题
K 代表梳理过程中零碎的知识点
U 代表未解决的问题
传统根轨迹的基本概念
Q1:根轨迹是什么
根轨迹是系统所有闭环极点的集合 它反映的是随着根轨迹增益 K ∗ K^* K∗从0变化到 + ∞ +\infty +∞时,闭环极点在复数域的变化
K1.1 稳定性和什么有关
- 稳定性指的是系统在扰动消失后,恢复到原来平衡状态的能力。即,对于理想脉冲 δ ( t ) \delta(t) δ(t),系统脉冲响应 c ( t ) c(t) c(t)应当满足 lim t → ∞ c ( t ) = 0 \lim_{t \to \infty} c(t)= 0 t→∞limc(t)=0
- 可以证明 线性系统稳定的充分必要条件是:闭环系统特征方程所有根均具有负实部,或者说,闭环传递函数极点均位于s左半平面
K1.2 根轨迹增益 K ∗ K^* K∗和开环增益 K K K有什么关系
开环增益 K K K为尾1,根轨迹增益 K ∗ K^* K∗为首1
Q2:出题形式/题目的已知量是什么
一般来说,题目会给出一个系统,开环传函为 G ( s ) G(s) G(s),反馈传函 H ( s ) H(s) H(s)均为已知【有时候是单位负反馈, H ( s ) = 1 H(s)=1 H(s)=1】
根据开环传函,可以确定闭环极点的一些信息
K2.1 闭环零极点和开环零极点的关系✨
- 开环根轨迹增益 K ∗ = K G ∗ K H ∗ K^*=K_G^*K_H^* K∗=KG∗KH∗。对于单位负反馈系统,闭环增益就是开环增益。
- 闭环传函 Φ ( s ) \Phi(s) Φ(s)的零点 是 开环传函零点及反馈传函极点的 K G ∗ K_G^* KG∗倍
- 闭环传函 Φ ( s ) \Phi(s) Φ(s)的极点与开环零点、开环极点、根轨迹增益 K ∗ K^* K∗均有关
Φ ( s ) = K G ∗ ∏ i = 1 f ( 开环 ) ( s − z i ) ∏ j = 1 h ( 反馈 ) ( s − p j ) ∏ i = 1 n ( 总 ) ( s − p i ) + K ∗ ∏ j = 1 m ( 总 ) ( s − z j ) \Phi(s)=\frac{K_{G}^{*} \prod_{i=1}^{f(开环)}\left(s-z_{i}\right) \prod_{j=1}^{h(反馈)}\left(s-p_{j}\right)}{\prod_{i=1}^{n(总)}\left(s-p_{i}\right)+K^{*} \prod_{j=1}^{m(总)}\left(s-z_{j}\right)} Φ(s)=∏i=1n(总)(s−pi)+K∗∏j=1m(总)(s−zj)KG∗∏i=1f(开环)(s−zi)∏j=1h(反馈)(s−pj)
Q3:怎么理解幅值/相角条件?
闭环传函的极点,应当满足 1 + G ( s ) H ( s ) = 0 1+G(s)H(s)=0 1+G(s)H(s)=0
幅值条件和相角条件如下
∣ G ( s ) H ( s ) ∣ = K ∗ ∣ s − z 1 ∣ ⋯ ∣ s − z m ∣ ∣ s − p 1 ∣ ∣ s − p 2 ∣ ⋯ ∣ s − p n ∣ = K ∗ ∏ i = 1 m ∣ ( s − z i ) ∣ ∏ j = 1 n ∣ ( s − p j ) ∣ = 1 ∠ G ( s ) H ( s ) = ∑ i = 1 m ∠ ( s − z i ) − ∑ j = 1 n ∠ ( s − p j ) = ( 2 k + 1 ) π \begin{array}{l} |G(s) H(s)|=\frac{K^{*}\left|s-z_{1}\right| \cdots\left|s-z_{m}\right|}{\left|s-p_{1}\right|\left|s-p_{2}\right| \cdots\left|s-p_{n}\right|}=K^{*} \frac{\prod_{i=1}^{m}\left|\left(s-z_{i}\right)\right|}{\prod_{j=1}^{n}\left|\left(s-p_{j}\right)\right|}=1 \\\\ \angle G(s) H(s)=\sum_{i=1}^{m} \angle\left(s-z_{i}\right)-\sum_{j=1}^{n} \angle\left(s-p_{j}\right)=(2 k+1) \pi \end{array} ∣G(s)H(s)∣=∣s−p1∣∣s−p2∣⋯∣s−pn∣K∗∣s−z1∣⋯∣s−zm∣=K∗∏j=1n∣(s−pj)∣∏i=1m∣(s−zi)∣=1∠G(s)H(s)=∑i=1m∠(s−zi)−∑j=1n∠(s−pj)=(2k+1)π
如何理解相角条件?
跟轨迹方程实际上是一个向量方程,因此可以从几何角度考虑。
s s s指向所有零点 z i z_i zi的向量与正实轴方向的夹角之和 - s s s指向所有极点 p j p_j pj的向量与正实轴方向的夹角之和 = 负实轴方向角度 ( 2 k + 1 ) π (2k+1)\pi (2k+1)π
K3.1 ∏ i = 1 n ( s − z i ) ∏ j = 1 m ( s − p j ) \frac{\prod_{i=1}^{n} (s-z_i)}{\prod_{j=1}^{m}(s-p_j)} ∏j=1m(s−pj)∏i=1n(s−zi)这类分式的夹角
化简后,该分式夹角即为“分子各项夹角 - 分母各项夹角”
K3.2 相角条件是确定 s s s平面根轨迹的充分必要条件
K3.3 需要确定根轨迹上某个点对应的 K ∗ K^* K∗时,才需要用到模值条件
系统性能分析
Q4A:增加开环零极点的作用
事实上,这块的概念比较抽象笼统,后期可以考虑结合相角裕度学习
开环零点:
一定程度上,增加开环零点,可以使闭环系统动态性能和稳定性都有所改善,根轨迹向左【零点处】弯曲【因为根轨迹会指向零点】
K4A.1 开环零点相当于KD比例微分控制
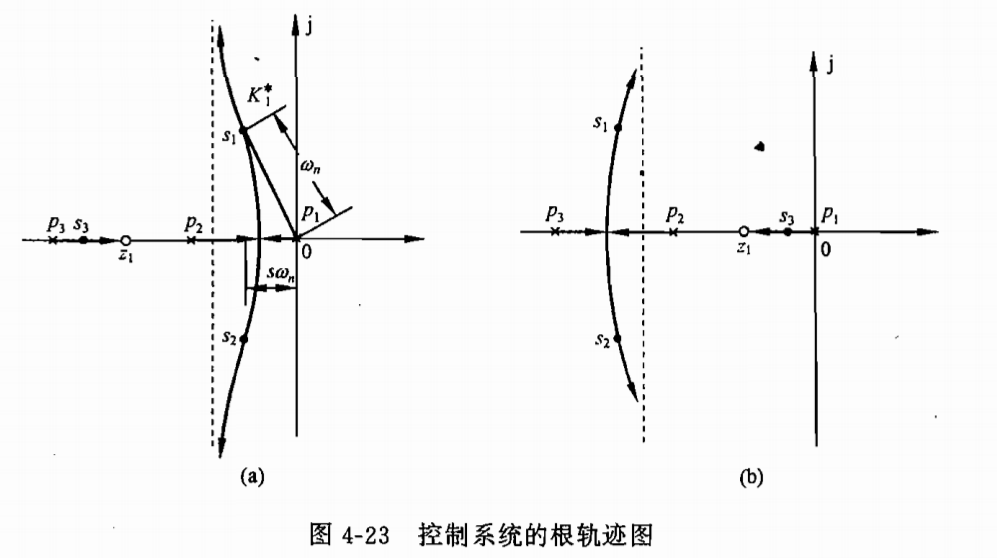
K4A.2 开环零点对系统稳定性和动态性能的影响有时相矛盾✨
如图所示,图(b)的稳定性更好,但是图(a)的动态性能优于图(b)
【因为图(a)的主导极点是共轭极点,响应快调节时间短;图(b)的主导极点在负实轴,等效一阶系统,响应速度慢调节时间长。】
开环极点:
开环极点会使得闭环系统动态性能变坏
Q4B:增加闭环零极点的作用
事实上,这块的概念比较抽象笼统,后期可以考虑结合相角裕度学习
闭环零点:
稳定性:
增加闭环零点不改变根轨迹,也不影响稳定性
动态性能:
增加闭环零点相当于减小系统的阻尼,从而使系统的过渡过程有超调的趋势,并且这种作用将随着闭环极点接近坐标原点的程度而增强。
闭环极点
靠近虚轴的极点被叫做主导极点【参考K4A.1分析】
闭环实数主导极点的作用,相当于增大系统的阻尼,使峰值时间滞后,超调量下降。
K4B.1 增加闭环零点不改变系统稳定性及根轨迹
理由很简单,这两者只跟系统闭环极点有关。
K4B.2 闭环实数极点意味着平滑,超调减少 复数极点意味着振荡
K4B.3 闭环实数零点使峰值时间提前,超调量增大,系统阻尼减小,越靠近原点效果越强
K4B.4 闭环实数极点使峰值时间滞后,超调量减小,系统阻尼增大,越靠近原点效果越强
UQ❓ 怎么理解闭环零极点的作用?
UQ2 什么是平滑滤波器
偶极子
如果闭环极点和闭环零点靠得很近,那么他们被称为偶极子。
只要偶极子不靠近坐标原点,他们对于系统动态性能的影响就很微小。
Q5 是否存在共轭(二阶)闭环极点不是主导极点的情况【如图】

是的,存在。见K4A.1分析
K5.1 输入信号极点不在主导极点的选择范围之内