自动控制原理(考研)习题篇--第三章(线性系统的时域分析法)

本博文基于自动控制原理习题解析(胡寿松第二版)，解答经典习题，总结解题规律，便于同学们的复习，该篇属于自动控制原理的习题篇，以习题为驱动，不做只懂理论不懂解题的人，因作者也是在复习考研，也是刚毕业的大学生，总结的东西难免会有所纰漏，如发现，请在评论区提醒，望共同进步，考研成功上岸！

---

---

1. 题目：试求下面系统的单位脉冲响应$c(t)$和单位阶跃响应$c(t)$，已知全部初始条件为零。
   $$0.04\ddot{c}(t)+0.24\dot{c}(t)+c(t)=r(t)$$
   考点分析：此类问题解决方法：先利用拉氏变换将微分方程转换为系统的传递函数，然后根据拉氏反变换求得系统的各类响应。
   解：
   由于初始条件为零，对微分方程两边进行拉氏变换可得：
   $$0.04s^{2}C(s)+0.24sC(s)+C(s)=R(s)$$
   则系统的传递函数为：
   $$\Phi (s)=\frac{C(s)}{R(s)}=\frac{1}{0.04s^2+0.24s+1}=\frac{25}{s^2+6s+25}$$
   $由\Phi (s)=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}的形式可以确定：$
   $${\omega }_n^2=25，2\zeta {\omega }_n=6$$
   $$则{\omega }_n=5，\zeta =0.6，{\omega }_d={\omega }_n\sqrt{1-{\zeta }^2}=4，\beta =\arctan (\frac{\sqrt{1-{\zeta }^2}}{\zeta })=53.2°$$
   当输入为单位脉冲信号时，$R(s)=1$，系统的单位脉冲响应：
   $$c(t)=\frac{{\omega }_n}{\sqrt{1-{\zeta }^2}}{e}^{-\zeta {\omega }_{n}t}\sin {\omega }_{d}t=6.25e^{-3t}\sin 4t，(t\ge 0)$$
   当输入为单位阶跃信号时，$R(s)=\frac{1}{s}$，系统的单位阶跃响应为：
   $$c(t)=1-\frac{1}{\sqrt{1-{\zeta }^2}}{e}^{-\zeta {\omega }_{n}t}\sin ({\omega }_{d}t+\beta )=1-1.25e^{-3t}\sin (4t+53.2°)，(t\ge 0)$$

---

---

2. 题目：已知二阶系统的单位阶跃响应为：$c(t)=10-12.5e^{-1.2t}\sin (1.6t+53.1°)$，试求系统的超调量$\sigma \%$、峰值时间$t_p$和调节时间$t_s$。
   考点分析：此类问题的解决方法：将二阶系统的单位阶跃响应的表达式与标准的表达式比较，解得系统的自然频率和阻尼比，然后运用这些参数计算动态性能指标。
   解：
   本题二阶系统的单位阶跃响应为：
   $$c(t)=10-12.5e^{-1.2t}\sin (1.6t+53.1°)=10[1-1.25e^{-1.2t}\sin (1.6t+53.1°)]$$
   由上式知，该二阶系统的放大系数是10，但放大系数不影响系统的动态性能，标准的二阶系统的单位阶跃响应为：
   $$c(t)=1-\frac{1}{\sqrt{1-{\zeta }^2}}{e}^{-\zeta {\omega }_{n}t}\sin ({\omega }_n\sqrt{1-{\zeta }^2}t+\beta )$$
   则有：
   $$\zeta {\omega }_n=1.2，\frac{1}{\sqrt{1-{\zeta }^2}}=1.25，{\omega }_n\sqrt{1-{\zeta }^2}=1.6，\beta =\arccos \zeta =53.1°$$
   解得：
   $$\zeta =0.6，{\omega }_n=2$$
   由于$0＜\zeta ＜1$，因此该系统为欠阻尼二阶系统，其动态性能指标为：
   $$超调量：\sigma \%=e^{-\pi \zeta \sqrt{1-{\zeta }^2}}\times 100\%=9.5\%$$
   $$峰值时间：t_p=\frac{\pi }{{\omega }_n\sqrt{1-{\zeta }^2}}=\frac{\pi }{2\times 0.8}=1.96s$$
   $$调节时间：t_s=\frac{3.5}{\zeta {\omega }_n}=\frac{3.5}{1.2}=2.92s，(\Delta =5\%)$$

---

---

3. 题目：设单位反馈系统的开环传递函数为：$G(s)=\frac{0.4s+1}{s(s+0.6)}$，试求系统在单位阶跃输入下的动态性能。
   解：
   由开环传递函数可得系统的闭环传递函数为：
   $$\Phi (s)=\frac{G(s)}{1+G(s)}=\frac{0.4(s+2.5)}{s^2+s+1}$$
   $从\Phi (s)的形式看，该系统是比例-微分控制二阶系统，其标准形式为：$
   $$\Phi (s)=\frac{{\omega }_n^2}{z}\cdot \frac{s+z}{s^2+2{\zeta }_d{\omega }_{n}s+{\omega }_n^2}$$
   由
   $$\frac{0.4s+1}{s^2+s+1}=\frac{{\omega }_n^2}{z}\cdot \frac{s+z}{s^2+2{\zeta }_d{\omega }_{n}s+{\omega }_n^2}$$
   可得：
   $$z=2.5，{\omega }_n=1，{\zeta }_d=0.5$$
   由于：
   $$r=\frac{\sqrt{z^2-2{\zeta }_d{\omega }_{n}z+{\omega }_n^2}}{z\sqrt{1-{\zeta }_d^2}}=1.007$$
   $$\psi =-\pi +\arctan (\frac{{\omega }_n\sqrt{1-{\zeta }_d^2}}{z-{\zeta }_d{\omega }_n})+\arctan (\frac{\sqrt{1-{\zeta }_d^2}}{{\zeta }_d})=-1.686$$
   $${\beta }_d=\arctan (\frac{\sqrt{1-{\zeta }_d^2}}{{\zeta }_d})=1.047$$
   动态性能指标为：
   $$峰值时间：t_p=\frac{{\beta }_d-\psi }{{\omega }_n\sqrt{1-{\zeta }_d^2}}=3.156s；$$
   $$超调量：\sigma \%=r\sqrt{1-{\zeta }_d^2}{e}^{-{\zeta }_d{\omega }_n{t}_p}\times 100\%=18.0\%$$
   $$调节时间：t_s=\frac{4+\frac{1}{2}\ln (z^2-2{\zeta }_d{\omega }_{n}z+{\omega }_n^2)-\ln z-\frac{1}{2}\ln (1-{\zeta }_d^2)}{{\zeta }_d{\omega }_n}=\frac{4+\ln r}{{\zeta }_d{\omega }_n}=8.01s，(\Delta =0.02)$$

---

---

4. 题目：已知控制系统的单位阶跃响应为：$c(t)=1+0.2e^{-60t}-1.2e^{-10t}$，试确定系统的阻尼比$\zeta$和自然频率${\omega }_n$。
   考点分析：要确定系统的阻尼比和自然频率，可以通过系统的闭环传递函数获得，系统的闭环传递函数是单位脉冲响应的拉氏变换，已知条件为系统的单位阶跃响应，可以将其微分得到单位脉冲响应，可求得结果。
   解：
   系统的单位脉冲响应为：
   $$c(t)=-12e^{-60t}+12e^{-10t}=12(e^{-10t}-e^{-60t})$$
   系统的闭环传递函数为：
   $$\Phi (s)=L[c(t)]=12(\frac{1}{s+10}-\frac{1}{s+60})=\frac{600}{s^2+70s+600}=\frac{{\omega }_n^2}{s^2+2\zeta {\omega }_{n}s+{\omega }_n^2}$$
   则系统的自然频率和阻尼比为：
   $${\omega }_n=\sqrt{600}=24.5，\zeta =\frac{70}{2\times \sqrt{600}}=1.43$$

---

---

5. 题目：试求下列各系统的自然频率和阻尼比，并列表比较其动态性能。
   
   考点分析：由结构图求传递函数，并求系统动态性能。
   解：
   图a系统，由图可知，闭环传递函数为：
   $${\Phi }_a(s)=\frac{1}{s^2+1}$$
   $此时，系统的自然频率{\omega }_n=1，阻尼比\zeta =0，系统为零阻尼系统，其单位阶跃响应为：$
   $$c(t)=1-\cos {\omega }_{n}t=1-\cos t$$
   因
   $$\frac{dc(t)}{dt}{|}_{t=t_p}=\sin t_p=0，(t_p=0，\pi ，2\pi ，\dots )$$
   取
   $$t_p=\pi =3.142s$$
   而
   $$c(t_p)=1-\cos t_p=2$$
   因此，
   $$\sigma \%=\frac{c(t_p)-c(\infty )}{c(\infty )}=100\%$$
   $对于等幅振荡的无阻尼系统，t_s不存在，也没有意义。$
   图b系统，由图可知，闭环传递函数为：
   $${\Phi }_b(s)=\frac{s+1}{s^2+s+1}$$
   $从{\Phi }_b(s)的形式可以看出，该系统是比例-微分控制二阶系统，其标准形式为：$
   $$\Phi (s)=\frac{{\omega }_n^2}{z}\cdot \frac{s+z}{s^2+2{\zeta }_d{\omega }_{n}s+{\omega }_n^2}$$
   $可得:z=1,{\omega }_n=1,{\zeta }_d=0.5$
   $由于：$
   $$r=\frac{\sqrt{z^2-2{\zeta }_d{\omega }_{n}z+{\omega }_n^2}}{z\sqrt{1-{\zeta }_d^2}}=1.155$$
   $$\psi =-\pi +\arctan (\frac{{\omega }_n\sqrt{1-{\zeta }_d^2}}{z-{\zeta }_d{\omega }_n})+\arctan (\frac{\sqrt{1-{\zeta }_d^2}}{{\zeta }_d})=-60°$$
   $${\beta }_d=\arctan (\frac{\sqrt{1-{\zeta }_d^2}}{{\zeta }_d})=60°$$
   $动态性能指标为：$
   $$峰值时间：t_p=\frac{{\beta }_d-\psi }{{\omega }_n\sqrt{1-{\zeta }_d^2}}=2.418s；$$
   $$超调量：\sigma \%=r\sqrt{1-{\zeta }_d^2}{e}^{-{\zeta }_d{\omega }_n{t}_p}\times 100\%=29.9\%$$
   $$调节时间：t_s=\frac{4+\ln r}{{\zeta }_d{\omega }_n}=8.3s，(\Delta =0.02)$$
   图c系统，由图可知，闭环传递函数为：
   $${\Phi }_c(s)=\frac{1}{s^2+s+1}$$
   $此时，系统的自然频率{\omega }_n=1，阻尼比\zeta =0.5，则系统性能指标为：$
   $$超调量：\sigma \%=e^{-\pi \zeta /\sqrt{1-{\zeta }^2}}\times 100\%=16.3\%$$
   $$峰值时间：t_p=\frac{\pi }{\omega \sqrt{1-{\zeta }^2}}=3.628s$$
   $$调节时间：t_s=\frac{4.4}{\zeta {\omega }_n}=8.8s，(\Delta =2\%)$$
   $性能指标比较如下：$

性能/系统	$(a)$	$(b)$	$(c)$
${\omega }_n$	1	1	1
$\zeta$	0	0.5	0.5
$t_p/s$	3.142	2.418	3.628
$\sigma /\%$	100	29.9	16.3
$t_s/s$	—	8.3	8.8

---

---

6. 题目：下图所示控制系统有两种不同的结构方案，其中$T>0$不可变，要求：
   (1) 在这两种方案中，应如何调整$K_1、K_2、K_3$，才能使系统获得较好的动态性能？
   (2) 比较说明两种结构方案的特点。
   
   考点分析：利用测速反馈和比例-微分控制控制来改善二阶系统的动态性能。
   解：
   $为了方便讨论，假设T=1$。
   $原系统，即K_3=0：$
   $开环传递函数为：$
   $$G_0(s)=\frac{K_1{K}_2}{s^2+s}$$
   $闭环传递函数为：$
   $${\Phi }_0(s)=\frac{K_1{K}_2}{s+s+K_1{K}_2}$$
   $方案a测速反馈控制系统：$
   $开环传递函数为：$
   $$G_a(s)=\frac{K_1{K}_2}{s^2+(1+K_2{K}_3)s}$$
   $闭环传递函数为：$
   $${\Phi }_a(s)=\frac{K_1{K}_2}{s^2+(1+K_2{K}_3)s+K_1{K}_2}$$
   $方案b比例-微分控制系统：$
   $开环传递函数为：$
   $$G_b(s)=\frac{K_2{K}_{3}s+K_1{K}_2}{s^2+s}$$
   $闭环传递函数为：$
   $${\Phi }_a(s)=G_b(s)=\frac{K_2{K}_{3}s+K_1{K}_2}{s^2+(1+K_2{K}_3)s+K_1{K}_2}$$
   $由三者的开环传递函数可知，原系统、测速反馈控制系统与比例-微分控制系统均为Ⅰ型系统，其静态速度误差系数分别为：$
   $$K_{v0}=K_1{K}_2，K_{va}=\frac{K_1{K}_2}{1+K_2{K}_3}，k_{vb}=K_1{K}_2$$
   $(1)参数调整措施。$
   $$\begin{gathered} 方案(a)测速反馈控制系统：在原有系统中引入速度反馈，在不影响系统的自然频率的同时可以增大系统的阻尼比， \\ 达到改善系统动态性能的目的，如减小超调量、加快调节时间等。测速反馈系数K_3的选择，要使阻尼比在0.4～0.8之间， \\ 从而满足给定的各项动态性能指标，但是，测速反馈会降低系统的开环增益，从而加大系统在斜坡输入时的稳态误差， \\ 因此必须考虑加大原系统的开环增益，然而，增加K_1又会导致阻尼比下降，从而使超调量加大，此时应该增加K_2。 \end{gathered}$$
   $$\begin{gathered} 方案(b)比例—微分控制系统：比例—微分控制可以增大系统的阻尼比，使超调量下降，调节时间缩短，且不影响系统的自然频率和常值稳态误差。 \\ 由于采用微分控制后，允许选取较高的开环增益，因此保证一定的动态性能条件下，可以减小稳态误差。 \\ 然而，增加K_1又会导致阻尼比下降，从而超调量加大，此时应该考虑增加K_2 \end{gathered}$$。
   $(2)方案特点。$
   $a.测速反馈控制与比例-微分控制都可以改善二阶系统的动态性能；$
   $$\begin{gathered} b.比例-微分控制对系统的开环增益和自然频率均无影响，测速反馈控制虽不影响自然频率， \\ 但会降低开环增益。因此，对于确定的常值稳态误差，测速反馈控制要求有较大的开环增益； \end{gathered}$$
   $$\begin{gathered} c.比例-微分控制的阻尼作用产生于系统的输入端误差信号的速度， \\ 而测速反馈控制的阻尼作用来源于系统输出端的响应的速度， \\ 因此，对于给定的开环增益和指令输入速度，后者对应较大的稳态误差值； \end{gathered}$$
   $d.比例-微分控制对噪声有明显的放大作用，当系统输入端噪声严重时，一般不宜选用比例-微分控制，测速反馈控制对系统输入端噪声有滤波作用。$

---

---

7. 题目：已知系统的特征方程如下，试求系统在$s$右半平面的根数及虚根值。
   $$s^6+4s^5-4s^4+4s^3-7s^2-8s+10=0$$
   考点分析：劳斯判据的特殊情况。
   解：
   劳斯表如下：

$s^6$	1	-4	-7	10
$s^5$	4	4	-8
$s^4$	-5	-5	10	($辅助方程F(s)=-5s^4-5s^2+10=0的系数$)
$s^3$	0(-20)	0(-10)		$(dF(s)/ds=-20s^3-10s=0的系数$)
$s^2$	-2.5	10
$s^1$	-90
$s^0$	10

$由上表可见，劳斯表中的第一列元素符号改变两次，所以系统在s右半平面有两个特征根，由于辅助方程-5s^4-5s^2+10=0的解为s_{1,2}=\pm \sqrt{2}j，s_{3,4}=\pm 1，因此系统的一对虚根为s_{1,2}=\pm \sqrt{2}j。$

---

---

8. 题目：已知单位负反馈系统的开环传递函数为：
   $$G(s)=\frac{K(0.5s+1)}{s(s+1)(0.5s^2+s+1)}$$
   试确定系统稳定的$K$值范围。
   考点分析：应用劳斯稳定判据确定参数取值范围。
   解：
   $由题设条件，该系统为单位负反馈系统，根据开环传递函数列出闭环系统的特征方程：$
   $D(s)=s(s+1)(0.5s^2+s+1)+K(0.5s+1)=s^4+3s^3+4s^2+(2+K)s+2K=0$
   $劳斯表如下：$

$s^4$	1	4	$2K$
$s^3$	3	$2+K$
$s^2$	$\frac{10-K}{3}$	$2K$
$s^1$	$\frac{20-10K-K^2}{(10-K)}$
$s^0$	$2K$

$根据劳斯稳定判据可得，若系统稳定，K需要满足如下方程组：$
$$\{\begin{array}{l}10-K>0\\ 20-10K-K^2=-(K-1.708)(K+11.708)>0\\ K>0\end{array}$$
$解上述方程组可得：K<10,-11.708<K<1.708,K>0$
$因此，当0<K<1.708时，闭环系统是稳定的。$

---

---

9. 题目：已知单位反馈系统的开环传递函数：
   $$G(s)=\frac{10(2s+1)}{s^2(s^2+6s+100)}$$
   试求输入为$r(t)=2+2t+t^2$时，系统的稳态误差。
   考点分析：系统稳态误差可以通过静态误差系数法或终值定理求解，但求解稳态误差前必须对系统稳定性进行判断。
   解：
   $由于系统为单位负反馈，根据开环传递函数可以求得闭环系统的特征方程：$
   $$D(s)=s^2(s^2+6s+100)+10(2s+1)=s^4+6s^3+100s^2+20s+10=0$$
   $由赫尔维茨判据可知，n=4，各项系数a_0=1,a_1=6,a_2=100,a_3=20,a_4=10均为正，且{\Delta }_2=a_1{a}_2-a_0{a}_3=580>0,以及{\Delta }_2>a_1^2{a}_4/a_3=18，因此，系统是稳定的。$
   $用终值定理来求解系统的稳态误差，有：$
   $$e_{ss}(\infty )=\underset{s\to 0}{\lim }sE(s)=\underset{s\to 0}{\lim }s\cdot \frac{1}{1+G(s)H(s)}\cdot R(s)=\underset{s\to 0}{\lim }sR(s)\cdot \frac{s^2(s^2+6s+100)}{s^2(s^2+6s+100)+10(2s+1)}$$
   $当系统输入是r(t)=2+2t+t^2时，R(s)=\frac{2}{s}+\frac{2}{s^2}+\frac{2}{s^3}=\frac{2(s^2+s+1)}{s^3}，因此$
   $$e_{ss}(\infty )=\underset{s\to 0}{\lim }s\cdot \frac{2(s^2+s+1)}{s^3}\cdot \frac{s^2(s^2+6s+100)}{s^2(s^2+6s+100)+10(2s+1)}=20$$

---

---

10. 题目：已知单位反馈系统的开环传递函数如下：
    $$G(s)=\frac{10(2s+1)(4s+1)}{s^2(s^2+2s+10)}$$
    试求位置误差系数$K_p$、速度误差系数$K_v$、加速度误差系数$K_a$。
    考点分析：根据静态误差系数的定义求三大误差系数。
    解：
    $$K_p=\underset{s\to 0}{\lim }G(s)H(s)=\underset{s\to 0}{\lim }\frac{10(2s+1)(4s+1)}{s^2(s^2+2s+10)}=\infty$$
    $$K_v=\underset{s\to 0}{\lim }sG(s)H(s)=\underset{s\to 0}{\lim }s\cdot \frac{10(2s+1)(4s+1)}{s^2(s^2+2s+10)}=\infty$$
    $$K_a=\underset{s\to 0}{\lim }{s}^{2}G(s)H(s)=\underset{s\to 0}{\lim }{s}^2\cdot \frac{10(2s+1)(4s+1)}{s^2(s^2+2s+10)}=1$$

---

---

11. 题目：设控制系统如下图，其中：
    $$G(s)=K_p+\frac{K}{s}，F(s)=\frac{1}{Js}$$
    输入$r(t)$及扰动$n_1(t)$和$n_2(t)$均为单位阶跃函数，试求：
    (1) 在$r(t)$作用下系统的稳态误差；
    (2) 在$n_1(t)$作用下系统的稳态误差；
    (3) 在$n_1(t)$和$n_2(t)$同时作用下系统的稳态误差。
    
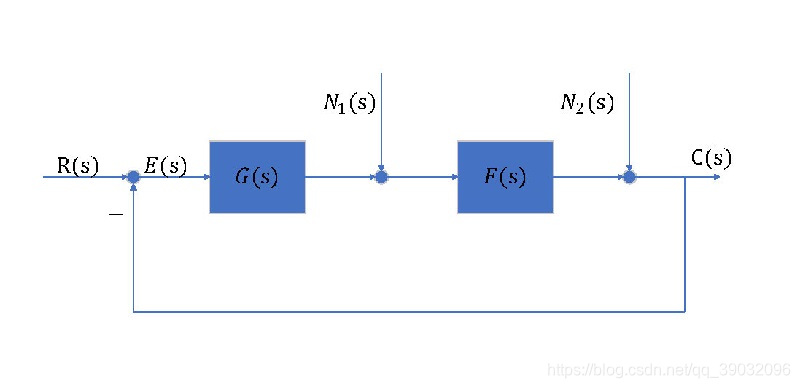
    考点分析：系统在输入及扰动作用下稳态误差的计算。
    解：
    $(1)r(t)作用下系统的稳态误差，误差传递函数为：$
    $${\Phi }_e(s)=\frac{E(s)}{R(s)}=\frac{1}{1+G(s)F(s)}$$
    $则$
    $$E(s)={\Phi }_e(s)R(s)=\frac{R(s)}{1+G(s)F(s)}$$
    $根据终值定理，系统的稳态误差为：$
    $$e_{ss}(\infty )=\underset{s\to 0}{\lim }sE(s)=\underset{s\to 0}{\lim }s\cdot \frac{R(s)}{1+G(s)F(s)}$$
    $由于$
    $$R(s)=\frac{1}{s}，G(s)=K_p+\frac{K}{s}，F(s)=\frac{1}{Js}$$
    $因此：$
    $$e_{ss}(\infty )=\underset{s\to 0}{\lim }s\cdot \frac{1}{1+(K_p+\frac{K}{s})\cdot \frac{1}{Js}}\cdot \frac{1}{s}=0$$
    $即在r(t)=1(t)作用下系统的稳态误差为0。$
    $(2)n_1(t)作用下系统的稳态误差，在N_1(s)作用下系统的输出为：$
    $$C_1(s)=\frac{F(s)}{1+G(s)F(s)}\cdot N_1(s)$$
    $故n_1(t)引起的误差函数为：$
    $$E_{n1}(s)=0-C_1(s)=-\frac{F(s)}{1+G(s)F(s)}\cdot N_1(s)$$
    $此时系统的稳态误差为：$
    $$e_{ssn1}(\infty )=\underset{s\to 0}{\lim }s{E}_{n1}(s)=\underset{s\to 0}{\lim }s\cdot [-\frac{F(s)}{1+G(s)F(s)}\cdot N_1(s)]$$
    $由于$
    $$N_1(s)=\frac{1}{s}，G(s)=K_p+\frac{K}{s}，F(s)=\frac{1}{Js}$$
    $因此$
    $$e_{ssn1}(\infty )=\underset{s\to 0}{\lim }[-\frac{s}{J{s}^2+K_{p}s+K}]=0$$
    $即在n_1(t)=1(t)作用下系统的稳态误差为0。$
    $(3)n_1(t)和n_2(t)同时作用下系统的稳态误差，在N_1(s)和N_2(s)分别作用下系统的误差函数：$
    $$E_{n1}(s)=0-C_1(s)=-\frac{F(s)}{1+G(s)F(s)}\cdot N_1(s)$$
    $$E_{n2}(s)=0-C_2(s)=-\frac{1}{1+G(s)F(s)}\cdot N_2(s)$$
    $因此，n_1(t)和n_2(t)同时作用下系统的误差为：$
    $$E_n(s)=E_{n1}(s)+E_{n2}(s)=-\frac{F(s)N_1(s)+N_2(s)}{1+G(s)F(s)}$$
    $此时系统的稳态误差为：$
    $$e_{ssn}(\infty )=\underset{s\to 0}{\lim }s{E}_n(s)=\underset{s\to 0}{\lim }s[-\frac{F(s)N_1(s)+N_2(s)}{1+G(s)F(s)}]=\underset{s\to 0}{\lim }[-\frac{J{s}^2+s}{J{s}^2+K_{p}s+K}]=0$$
    $即在n_1(t)=1(t)和n_2(t)=1(t)同时作用下系统的稳态误差为0。$

---

---

12. 题目：设随动系统的微分方程为：
    $$\{\begin{array}{l}{T}_1\frac{d^{2}c(t)}{d{t}^2}+\frac{dc(t)}{dt}=K_{2}u(t)\\ \\ u(t)=K_1[r(t)-b(t)]\\ \\ T_2\frac{db(t)}{dt}+b(t)=c(t)\end{array}$$
    其中，$T_1、T_2$和$K_2$为正常数。若要求$r(t)=1+t$时，$c(t)$对$r(t)$的稳态误差不大于正常数${\epsilon }_0$，试问$K_1$应满足什么条件？已知全部初始条件为零。
    考点分析：研究系统参数选择和系统稳态误差的关系，注意，首先考虑参数选择和系统稳定性的关系。
    解：
    $(1)系统的结构图。对题设给定系统的微分方程进行拉氏变换，有：$
    $$\{\begin{array}{l}(T_1{s}^2+s)C(s)=K_{2}U(s)\\ \\ U(s)=K_1(s)[R(s)-B(s)]\\ \\ (T_{2}s+1)B(s)=C(s)\end{array}$$
    $由上述方程式画出系统的结构图,如下图：$
    
    $(2)系统参数选择与系统稳定性的关系，由结构图得闭环传递函数：$
    $$\Phi (s)=\frac{K_1{K}_2(T_{2}s+1)}{s(T_{1}s+1)(T_{2}s+1)+K_1{K}_2}$$
    $闭环特征方程为：$
    $$D(s)=T_1{T}_2{s}^3+(T_1+T_2)s^2+s+K_1{K}_2=0$$
    $列劳斯表如下：$

$s^3$	$T_1{T}_2$	1
$s^2$	$T_1+T_2$	$K_1{K}_2$
$s^1$	$\frac{(T_1+T_2)-T_1{T}_2{K}_1{K}_2}{T_1+T_2}$
$s^0$	$K_1{K}_2$

$在T_1、T_2和K_2为正常数条件下，使闭环系统稳定的充要条件为：$
$$0<K_1<\frac{T_1+T_2}{K_2{T}_1{T}_2}$$
$(3)系统参数选择与系统稳态误差的关系，定义系统的误差为E(s)=R(s)-C(s)，则$
$${\Phi }_e(s)=\frac{E(s)}{R(s)}=1-\Phi (s)=\frac{s[T_1{T}_2{s}^2+(T_1+T_2)s+(1-K_1{K}_2{T}_2)]}{T_1{T}_2{s}^3+(T_1+T_2)s^2+s+K_1{K}_2}$$
$由于$
$$r(t)=1+t$$
$因此$
$$R(s)=\frac{1}{s}+\frac{1}{s^2}=\frac{s+1}{s^2}$$
$由终值定理得$
$$e_{ss}(\infty )=\underset{s\to 0}{\lim }sE(s)=\underset{s\to 0}{\lim }s\cdot \frac{s[T_1{T}_2{s}^2+(T_1+T_2)s+(1-K_1{K}_2{T}_2)]}{T_1{T}_2{s}^3+(T_1+T_2)s^2+s+K_1{K}_2}\cdot \frac{s+1}{s^2}=\frac{1-K_1{K}_2{T}_2}{K_1{K}_2}$$
$令e_{ss}(\infty )=\frac{1-K_1{K}_2{T}_2}{K_1{K}_2}\le {\epsilon }_0$
$可得：$
$$K_1\ge \frac{1}{K_2(T_2+{\epsilon }_0)}$$
$考虑到使系统稳定的充要条件为：$
$$0<K_1<\frac{T_1+T_2}{K_2{T}_1{T}_2}$$
$因此满足题意要求的K_1值为：$
$$\frac{1}{K_2(T_2+{\epsilon }_0)}\le K_1<\frac{T_1+T_2}{K_2{T}_1{T}_2}$$