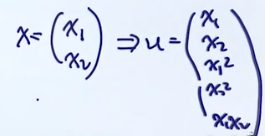线性分类器

分清回归和分类

之前写了逻辑回归，这里又提到线性分类，有点懵，先把百度得到的知识贴一下：
先讲回归和分类。这个好说回归是用来做预测具体数值的，例如：ng的预测房价问题。
分类顾名思义就是用来做分类的，例如：根据数据预测你买房还是不买房，这个是二分类，还有多分类。
那逻辑回归的时候明明是用来解决分类问题的啊，这里就是比较懵的地方。
这算是一个约定俗成的一个失误性命名吗?
非也，逻辑回归的主体还是回归操作：回归对象是sigmoid函数，它将输入映射为一个处于0到1之间的小数。得到这个0到1之间的小数之后人为将其解读成概率，然后根据事先设定的阈值进行分类。
回归操作的工作量在整个Logistic Regression中保守估计也得超过95%。以这个算法的主体—逻辑回归来命名算法是无可厚非的。也就是回归操作后面接转换操作，变成分类操作。
几个名词：
线性回归：Linear Regression
逻辑回归：Logistic Regression
线性分类器：Linear Classifier

Linear Classifier

由于后面要从这个东西切入到SVM，所以先把这个东西讲下，这个其实很简单。
假设有数据集：
$D=\{(x_1,y_1),(x_2,y_2),...,(x_n,y_n)\},y\in\{-1,1\},i=1,2,...,n$
参数：
$\theta=\{w,b\}$
决策边界：
$w^T\cdot x+b=0$
判断条件表达式：
$\begin{cases} & w^T\cdot x+b\geq0时，y_i=1\\ & w^T\cdot x+b\leq0时，y_i=-1 \end{cases}$
在这里插入图片描述
合起来：
$(w^T\cdot x+b)\cdot y_i\geq0$

Max margin method

在这里插入图片描述
这里三个分类边界，明显2号要最好，因为它的安全区域最大，对于类似绿色圆圈的噪音扰动perturbation，2号线的robust鲁棒性最好。这个现象也叫：robust to the perturbation。
SVM就是这么样一个方法。先看margin的数学表示：

Margin的表示

在这里插入图片描述
先看上图中的表示方式：
1、分界线的方程我们知道是 $w^T\cdot x+b=0$
但是为什么两边是 $w^T\cdot x+b=1$ 和 $w^T\cdot x+b=-1$ ？
其实是跟单位向量一个原理，无论是 $w^T\cdot x+b=10$ 还是 $w^T\cdot x+b=100$ ，我们最终都可以看做是 $w^T\cdot x+b=1$ 进行平移后的结果。
2、向量w的方向与分界线为什么是垂直的？
如上图所示，假设分界线上有两个点： $x_1,x_2$ ，那么我们可以写出这两个点满足：
$\begin{cases} & w^T\cdot x_1+b=0 \\ & w^T\cdot x_2+b=0 \end{cases}$
两式相减得：
$w(x_1-x_2)=0$
这个表示w与 $x_1-x_2$ 垂直， $x_1,x_2$ 是分界线，所以命题得证。
3、Margin的表示
假设 $x_+,x_-$ 是w上两个点，且分别与两个margin边界相交。因此根据这些条件有：
$\begin{cases} & w^T\cdot x_++b=1 \\ & w^T\cdot x_-+b=-1\\ &x_+=x_-+\lambda w\\ \end{cases}\tag1$
先求 $\lambda$ ，把（3）中的第三个式子带入第一个式子：
$w^T\cdot (x_-+\lambda w)+b=1\to w^T\cdot x_-+\lambda w^Tw+b=1$
整合第二个式子：
$\lambda=\cfrac{2}{ w^Tw}$
由于 $x_+,x_-$ 是w上两个点：
$margin=|x_+-x_-|$
由第三式子：
$margin=|\lambda w|=||\lambda w||=\lambda ||w||$
再把 $\lambda$ 带入：
$margin=\cfrac{2}{ w^Tw}||w||=\cfrac{2}{ ||w||}$
也就是说我们的目标是
$Maximize\space \cfrac{2}{ ||w||}$

SVM Objective:Hard Constraint

根据上面的结论，可以写出来SVM的目标函数：
$\begin{cases} & Maximize\space \cfrac{2}{ ||w||} \\ &s.t. \space \space \space w^T\cdot x_i+b\geq 1,if \space y_i=1\\ &\quad \quad w^T\cdot x_i+b\leq -1,if \space y_i=-1\\ \end{cases}$
按我们的惯例，一般都是求最小值：
所以
$Maximize\space \cfrac{2}{ ||w||}\to Minimize ||w||\to Minimize ||w||^2$
写起来就是：
$\begin{cases} & Minimize ||w||^2 \\ &s.t. \space \space \space w^T\cdot x_i+b\geq 1,if \space y_i=1\\ &\quad \quad w^T\cdot x_i+b\leq -1,if \space y_i=-1\\ \end{cases}$
硬约束应该都知道，就是margin内部是不允许有样本点的，所有点都要在安全区域外。
最后把约束条件合并：
$\begin{cases} & Minimize ||w||^2 \\ &s.t. \space \space \space (w^T\cdot x_i+b)y_i\geq 1\\ \end{cases}$
为了求导方便，一般会加一个系数：
$\begin{cases} & Minimize \cfrac{1}{2}||w||^2 \\ &s.t. \space \space \space (w^T\cdot x_i+b)y_i-1\geq 0\\ \end{cases}$

SVM Objective:Soft Constraint

采用硬约束会有下面的问题：
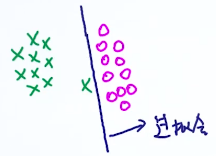
在这里插入图片描述
接下来，我们把硬限制或者说硬分类转换为软分类，也就是允许有错误的分类在安全区域，甚至在错误的分类线外。
我们只需要把约束条件改一改，因此条件中指明了分类必须在安全区域外。修改后变成：
$\begin{cases} & Minimize ||w||^2 \\ &s.t. \space \space \space (w^T\cdot x_i+b)y_i\geq 1-\varepsilon_i,\varepsilon_i\geq0\\ \end{cases}$
$\varepsilon_i$ 实际上是degree of mistake，就是犯了多大的错误（正确的叫法：slack variable，中文：松弛因子）。当然我们希望这个犯错越小越好，因此可以在目标函数中加入一项，进行约束：
$\begin{cases} & Minimize ||w||^2 +\lambda\sum_{i=1}^n\varepsilon_i\\ &s.t. \space \space \space (w^T\cdot x_i+b)y_i\geq 1-\varepsilon_i,\varepsilon_i\geq0\\ \end{cases}$
其中 $\lambda$ 是一个平衡参数，当 $\lambda\to\infty$ 的时候，也就是整个目标函数不允许犯错，因为一旦有错误就会被 $\lambda$ 放大。

Hinge Loss

这里看看Hinge Loss怎么来的，顺便把SVM最终的目标函数样式写出来。
先讲思路，一般像上面那种的带有约束条件的目标函数，我们都是要想KKT条件的解决套路来走，就是要想办法把约束条件融入到目标函数中。
由于我们要最小化 $||w||^2 +\lambda\sum_{i=1}^n\varepsilon_i$
因此就是要使得 $\varepsilon_i$ 尽量小，由约束可知， $\varepsilon_i$ 是有一个最小值的
$\varepsilon_i\geq1-(w^T\cdot x_i+b)y_i$
就是： $\varepsilon_i=1-(w^T\cdot x_i+b)y_i$
这里还有一个补充条件，就是 $\varepsilon_i\geq0 \to 1-(w^T\cdot x_i+b)y_i\geq0$
因为，如果是 $1-(w^T\cdot x_i+b)y_i\leq0\to (w^T\cdot x_i+b)y_i\leq1$
就变成了硬约束的条件了，不符合软约束的假设。
那么现在我们可以把目标函数写成：
$Minimize ||w||^2+\lambda\sum_{i=1}^nmax(0,1-(w^T\cdot x_i+b)y_i)$
其中：
$\begin{cases} & max(0,x):if\space x<0\to0\\ &\quad\quad\quad\quad\quad if\space x>0\to x\\ \end{cases}$
上面的 $max(0,1-(w^T\cdot x_i+b)y_i)$ 也叫Hinge Loss
到这里推导就差不多了，后面再往下就是用梯度下降来求解最优解。目前讨论的是用线性方程来分割样本，所以属于线性SVM。后面还会有非线性的SVM，就是加入卷积核的SVM，还有就是李宏毅课程里面讲的structed SVM。

Stochastic Gradient Descent for Hinge Loss Objective

观察目标函数：
$Minimize ||w||^2+\lambda\sum_{i=1}^nmax(0,1-(w^T\cdot x_i+b)y_i)$
根据在逻辑回归中的分析，我们发现，其实 $Minimize ||w||^2$ 是正则项， $\lambda\sum_{i=1}^nmax(0,1-(w^T\cdot x_i+b)y_i)$ 才是损失函数。
下面开始计算，首先初始化参数： $w_0,b_0$
然后循环所有样本：for i in 1…n
然后分情况进行讨论：
当 $1-(w^T\cdot x_i+b)y_i\leq 0$ 的时候，这个时候max的值为0，所以这项是不会有梯度产生的，那么只有前面的正则项参与梯度计算，计算公式为：
$w^*=w-\eta_t\cdot 2w$
当 $1-(w^T\cdot x_i+b)y_i>0$ 的时候，分别求损失函数对w和b的偏导。
$w^*=w-\eta_t\cdot(2w+\lambda\cfrac{\partial{(1-(w^T\cdot x_i+b)y_i})}{\partial{w}})$
$b^*=b-\eta_t\cdot(\lambda\cfrac{\partial{(1-(w^T\cdot x_i+b)y_i})}{\partial{b}})$

Disadvantages of Linear SVM

由于线性SVM的决策边界都是线性的，因此下面的场景线性SVM的效果不好
在这里插入图片描述
解决方案：
1、使用非线性模型，例如：NN
2、将数据映射到高维空间，再学习一个线性的模型。

Mapping Feature to High Dimensional Space

下面来看看这个东西怎么来做：
在这里插入图片描述
也就是把原来的特征做一些加减乘除，变成更多的特征，例如：

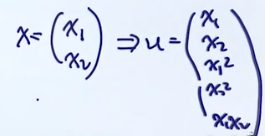
也就是变化后的特征空间维度D’要比原来的D要大得多。
那么现在的任务也从原来的： $f(x)\to y$
变成了： $f(\phi(x))\to y$ 或者写成： $f(u)\to y$
其中x是D维， $u=\phi(x)$ 是D‘维的。
这种方法在实操的时候有一个问题：时间复杂度增加。
例如原来的D=10，新的D‘=1000，那么时间复杂度也是按这个比例变化：O(10)->O(1000)
这里的时间复杂度的增加是包含两部分的工作的，其一是从低维特征向量转换为高维特征向量的增加，其二是在高维空间训练分类器的增加。
解决这个问题的方法就是核函数（kernel trick），它的思想就是把上面的转换维度和构造分类器两个事情结合到一起。使得时间的复杂度没有明显的增加。