回顾前面的SVM分类模型中，我们的目标函数是让
最小，同时让各个训练集中的点尽可能远离自己类别一边的支持向量，即
；若加入一个松弛变量
，则目标函数变为
，对应约束条件变为
。
线性支持回归也是尽量将训练集拟合到一个线性模型
。但是损失不是使用常用的均方差作为损失函数，而是定义一个常量，对于某一个点
，如果
，则认定为没有损失。若
，则对应的损失为
。
这个损失和均方差的区别在于，
就会有损失。
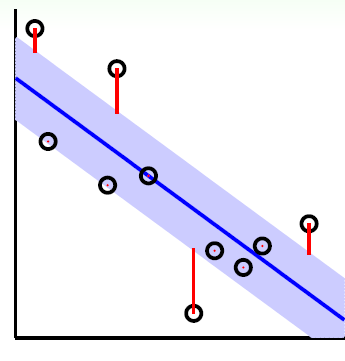
如图蓝色透明带内的点是没有损失的，而带外的红色点有损失，损失为红线的长度。处于透明带边界的点为此时的支持向量。
于是损失函数度量为：
接下来理解SVR的目标函数：
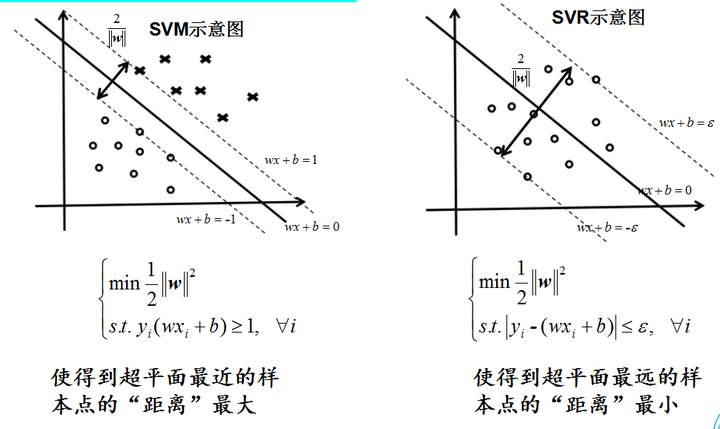
可以看到SVM的目标函数和SVR的目标函数一致。SVM希望支持向量到超平面的距离尽可能的大，最后由最大化几何间隔
推出了
。而SVR，由于刚才解释了损失函数，当处于“带内”的时候，损失不计。我们为了尽量让损失减少，所以想要增加“透明带”的“宽度”，而在边缘上的点就是支持向量，支持向量到超平面的距离就是几何间隔，于是问题又回到了，也就是。
现在我们的目标函数可以定义如下：
这个地方已经引入了映射，可在后面引入核函数。也就是说线性支持回归扩展到了非线性。
类似于SVM的软间隔引入了松弛变量，支持回归也可以引入松弛变量，但由于是绝对值，所以要引入两个松弛变量
。
拉格朗日函数的形式如下：
，均为拉格朗日系数。
这个优化目标满足KKT，和前面一样，可以转化为对偶问题：
先求优化函数极小，对应求偏导：
将上式代入消去对应变量，最终得到：
将目标函数取负，转为与SVM相似的目标函数：
接着还是用SMO算法求出对应的
，进而由
求出ω。
同样由KKT对偶互补条件找到所有支持向量，然后找到所有的b，最终求得平均值即为最后的b。
关于模型不受“带内”的点影响（稀疏性）
回归时，KKT对偶互补条件为：
当点在带内时，
，此时认定松弛向量
，这就导致
不为0，由对偶互补条件可知，
。
回忆ω的解析表达式，此时
为0。这就意味着，带内的点不对ω的构成产生影响，也就是说，误差范围内的点，不对模型产生影响，而仅仅是边缘上的支持向量，才对模型产生影响。这一点会联想到SVM，SVM的构成也只与支持向量有关，而与远离的点没有关系。
支持向量机小结
主要优点：
- 适合解决高维的分类和回归问题
- 仅仅使用一部分支持向量来做超平面的决策，不依赖全部数据
- 大量的核函数可以灵活运用于解决各种非线性的分类回归问题
主要缺点：
- 如果特征维度远大于样本数，则SVM表现一般
- SVM在样本量非常大时，核函数映射维度非常高，计算量过大，不太适合使用
- 非线性的核函数选择没有通用标准，难以选择
- 对缺失数据敏感
逻辑回归与支持向量机的区别与联系
联系：
- LR和SVM都可以用于处理分类，一般用于二分类，在改进情况下可用于多分类
- 都可以加入正则化项，关于SVM如何理解正则化项可以看知乎高赞回答https://www.zhihu.com/question/30230784?sort=created
区别：
- LR是参数模型（有限个参数来确定一个模型，比如样本维度为N，则假定N个参数），SVM型是非参数模型（非常多的参数，比如SVM中的α的数目和样本数目有关；当然前面提到了稀疏性，说明SVM也是稀疏模型）
- LR是logistical loss,SVM是hinge loss，这两个损失都是增大对分类影响较大的数据点的权重，减少与分类关系较小的数据点的权重
- SVM的处理方法是只考虑support vectors，也就是和分类最相关的少数点，去学习分类器。而逻辑回归通过非线性映射，大大减少了离分类平面较远的点的权重，相对提升了与分类最相关的数据点的权重。
- 逻辑回归的模型更简单易于理解，大规模分类时较方便；SVM理解相对复杂，但转化为对偶问题后，分类只需要计算少数几个支持向量的距离，在进行复杂核函数计算时优势很明显，能大大简化模型和计算
- LR能做到SVM能做，准确率有区别，但SVM能做的LR可能做不了（比如回归）
- LR受所有数据点的影响，数据不同类别处于极其不平衡的状态，一般需要先对数据做平衡处理；Linear SVM不直接依赖数据分布，分类平面不受一类点影响
- Linear SVM依赖数据表达的距离测度，所以需要对数据先做标准化；LR不受影响
- Linear SVM依赖惩罚项的系数，实验中需要做交叉验证
