分类器设计之线性分类器和线性SVM(含Matlab代码)

对于高维空间的两类问题，最直接的方法是找到一个最佳的分类超平面，使得 $w^Tx_i+b>0$ 并且 $w^Tx_j+b<0$ ,对于所有的正负训练样本 $x_1,x_2,...,x_n$ 和 $y_1,y_2,...,y_m$ . 因此，以上问题可以表达为：

$\LARGE \begin{align*} \text{P0: } &\text{minimize}& &0& \\ &\text{subject to}& &w^Tx_i+b>0,i=1,....,n& \\ &&&w^Ty_j+b<0,j=1,....,n & \end{align*}$

问题P0可以转化为

$\LARGE \begin{align*} \text{P1: } &\text{minimize}& &0& \\ &\text{subject to}& &w^Tx_i+b\ge\epsilon,i=1,....,n& \\ &&&w^Ty_j+b\le-\epsilon,j=1,....,n &\\ &&&\epsilon>0& \end{align*}$

两边除以\epsilon，并且做变量替换，最终得到下面的线性规化（linear programming）问题：

$\LARGE \begin{align*} \text{P2: } &\text{minimize}& &0& \\ &\text{subject to}& &w^Tx_i+b\ge1,i=1,....,n& \\ &&&w^Ty_j+b\le-1,j=1,....,n & \end{align*}$

线性规化问题P2事实上是一个存在性问题(feasibility problem)。通过Matlab的linprog函数可以解。具体解决有很多，此处暂不作论述。只要两类问题是严格可分的，则上述问题的解就存在，并不不是唯一：空间中存在无数多个超平面能将正负样本分开。从数学上理解，P2是smooth non-strictly convex问题，本身要么没有解，要么存在多个解。

下面用Matlab程序来演示线性分类器问题（以二维数据为例）

%%
clc;
clear;
close all;
%% generate random data
shift = 3;
n = 200;
m=200;
d = 2;
sigma = 1;
x = randn(d,n)-shift;
y = randn(d,m)*sigma+shift;
%%
%show the data
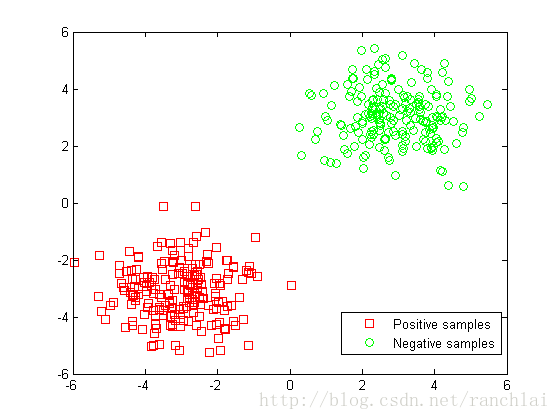
figure;
plot(x(1,:),x(2,:),'rs');
hold on;
plot(y(1,:),y(2,:),'Go');
legend('Positive samples','Negative samples');

%% training...
%Linear programming
for i=1:n
A(i,:) = [-x(:,i)',-1];
end
for i=1:m
A(i+n,:) = [y(:,i)',1];
end
c = ones(n+m,1)*(-1);
w = linprog(zeros(d+1,1),A,c);
hold on;
%% visualize the classification area
x1 = -shift-2:0.1:shift+2*sigma;
y1 = (-w(3)-w(1)*x1)/w(2);
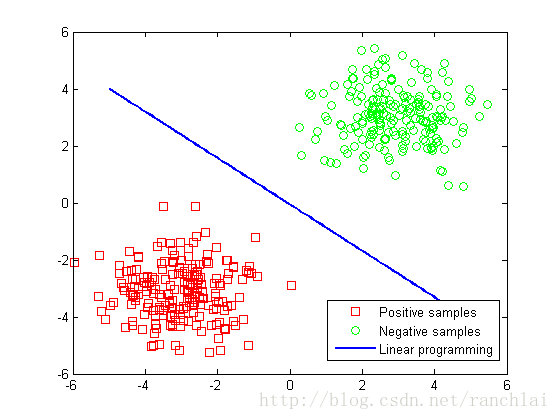
plot(x1,y1,'-','LineWidth',2);
legend('Positive samples','Negative samples','Linear programming');

由于采用线性规化来解线性可分问题存在无数多个解，那么哪个一解是最优的呢？我们希望找到一个超平面，使得该平面前后平移d的距离后分类碰到正负样本并且使d最大化。2*d 即为以下两个平面之间的距离:

$\LARGE \begin{align*} && &w^Tx+b=1& \\ &&&w^Tx+b=-1& \end{align*}$

这两个平面的距离为：

$\LARGE 2d=\frac{2}{||w||}$

因此，线性规化问题可以进一步加强为下面的二次规划问题：

$\LARGE \begin{align*} \text{P3: } &\text{maximize}& &d=\frac{1}{||w||}& \\ &\text{subject to}& &w^Tx_i+b\ge1,i=1,....,n& \\ &&&w^Ty_j+b\le1,j=1,....,n & \end{align*}$

即等价于：

$\LARGE \begin{align*} \text{P4: } &\text{minimize}& &w^Tw& \\ &\text{subject to}& &w^Tx_i+b\ge1,i=1,....,n& \\ &&&w^Ty_j+b\le1,j=1,....,n & \end{align*}$

以上的问题是strictly convex 问题。强大的SVM分类器即由此演化而来（结合核方法VC维理论）对于两类线性可分问题，上述问题存在唯一的解。具体解法在此同样暂不讲解，有兴趣可参考wiki：http://en.wikipedia.org/wiki/Quadratic_programming

下面对同样的二维数据进行分类：

%% svm
H = eye(d+1);
H(d+1,d+1) = 0;
w = quadprog(H,zeros(d+1,1),A,c);
hold on;
x1 = -shift-2:0.1:shift+2*sigma;
y1 = (-w(3)-w(1)*x1)/w(2);
plot(x1,y1,'g-','LineWidth',2);
y1 = (-1-w(3)-w(1)*x1)/w(2);
plot(x1,y1,'g-','LineWidth',2);
y1 = (1-w(3)-w(1)*x1)/w(2);
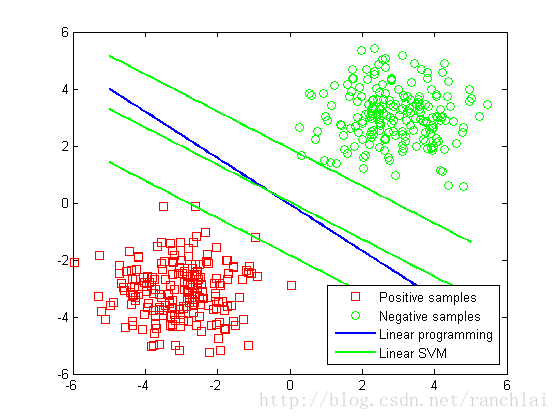
plot(x1,y1,'g-','LineWidth',2);
legend('Positive samples','Negative samples','Linear programming','Linear SVM');

从上图可见，线性SVM分类的效果要好于线性分类器。

PS：本文所有代码可在http://download.csdn.net/detail/ranchlai/6009209下载。

分类器设计之线性分类器和线性SVM(含Matlab代码)

猜你喜欢