最近在B站翻到了一位大神的线性代数教学视频,全部看完之后感觉受益匪浅,所以打算做一下笔记,时时回顾,防止忘记。
这是原作视频链接地址:https://www.bilibili.com/video/BV1ys411472E
各位看官老爷如果有空的话可以去原作视频看一看,保证不会后悔(# ^ . ^ #)
以下是笔记内容:
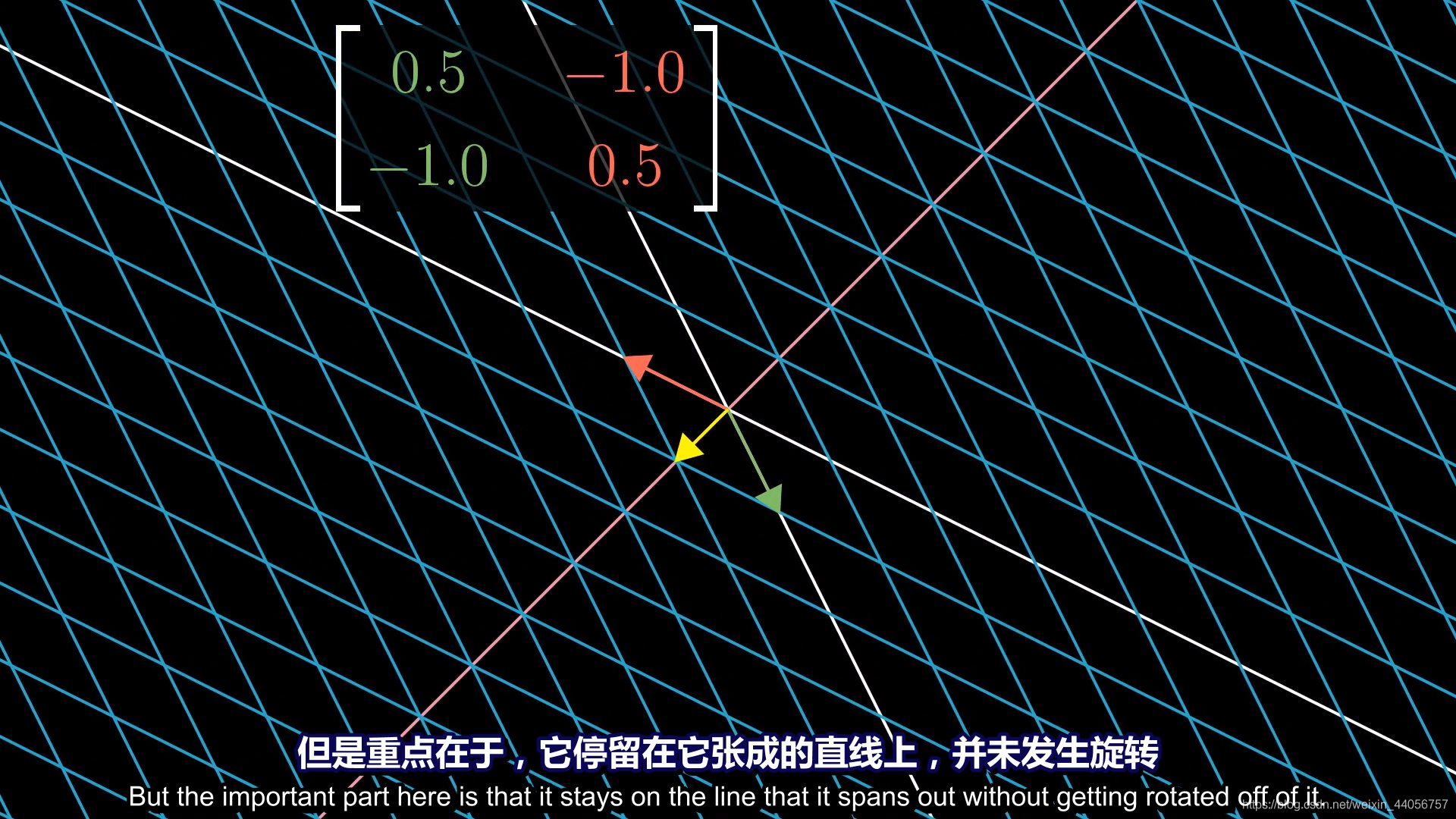
- 在一个线性变换中,大部分向量经过变换后偏离了它原本所在的直线,但是有少部分向量仍然在它原本所在的直线上,比如说一个线性变换将i-hat的坐标由(1,0)变为(2,0)则x轴上的所有向量都没有偏离它原本所在的直线。这些向量就被称为特征向量,这些向量变为原来的多少倍,即被缩放的比例因子被称为特征值。特征值当然可以为负。
- 特征向量的一个用处在于,对于三维空间中的一个旋转,如果找到这个旋转的特征向量,那这个向量就是旋转轴。
- 考虑三维空间按某一轴旋转比考虑3x3的矩阵要简单的多,另外特征向量的特征值必须是1,因为旋转不缩放任何一个向量。

上图中A是变换矩阵,V是特征向量,λ是特征值。

- 由此可以推出结论:当且仅当一个矩阵代表的线性变换将空间压缩到更低维度时才存在一个向量应用线性变换后为零向量。同时还存在着没有实数解即特征值为虚数的情况,这种情况一般是对应着旋转,比如二维空间绕着yaw轴旋转。
- 还可能出现只有一个特征值,但是特征向量不止在一条直线上的情况,比如i-hat和j-hat同时放大相同的倍数。
- 对角矩阵就是所有基向量都是特征向量。矩阵的对角元素就是对应的特征值。对角矩阵自己与自己相乘更好计算,因为对角矩阵仅仅让基向量与某个特征值相乘。如果基向量有两个以上且其中两个可以线性无关,则可以变换坐标系,使得特征向量就是基向量。(即对角化)
- 一组基向量(同样是特征向量)构成的集合被称为一组特征基。
以上就是这节笔记的全部内容了,欢迎大家在评论区互相讨论,如果有什么不对的地方也欢迎批评指正^ _ ^
