吴恩达|机器学习作业1.0单变量线性回归

1.0.单变量线性回归

1）题目：

在本部分的练习中，您将使用一个变量实现线性回归，以预测食品卡车的利润。假设你是一家餐馆的首席执行官，正在考虑不同的城市开设一个新的分店。该连锁店已经在各个城市拥有卡车，而且你有来自城市的利润和人口数据。
您希望使用这些数据来帮助您选择将哪个城市扩展到下一个城市。
x表示人口数据，y表示利润，一共97行数据。
数据链接: https://pan.baidu.com/s/1-u0iDFDibZc6tTGGx9_wnQ 提取码: 351j

注意：Python中可以用numpy的load函数读取数据，也可以用pandas的read函数读取，区别在于numpy读取的数据以array的形式而pandas以dataframe的形式，也就是在pandas中是matrix而不是array，但两者可以利用函数互相转化。
dataframe的优势是可以对数据进行很多操作，例如缺失值处理、合并或截取数据等。但是要想进行矩阵运算，先需要把dataframe转化为矩阵，例如x = x.values，再进行运算。但在array中就可以直接操作，注意这里的乘法和array通用，也是.dot()或者@。

2）知识点概括：

机器学习可分为：

• 监督学习（supervised learning）：
  回归（regression）：大量数据中得到连续数据的预测值
  分类（classification）：得到离散的预测值

• 无监督学习（unsupervised learning）：
  聚类（clustering）：（自动分类）

关于单变量线性回归：

• 假设（hypothesis） $h_\theta(x)=\theta_0+\theta_1x$ 也就是拟合曲线方程，它是输入值的函数
• 代价函数（cost function） $J(\theta)={1\over {2m}}\sum_{i=1}^m{(h_\theta(x^{(i)})-y^{(i)})^2}$ 在这里对于单变量线性回归也就是平方误差函数（squared error function），它是参数的函数。
• 梯度下降（gradient descent） $\theta_j:=\theta_j-\alpha {\partial \over \partial\theta_j}J(\theta)$（这里有几个参数就有几个方程，需要同时更新）用来求解代价函数（cost function）的最小值。
  一般是赋予参数初始值，通过不断改变参数得到代价函数的最小值或局部极小值。
  $\alpha$称为学习速率（learning rate）控制了以多大的幅度更新参数，正数，太小导致收敛速度很慢，太大导致无法收敛或者发散。
  Batch梯度下降算法的每一步梯度下降都历遍了整个训练集，因为 $\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2$
• 正规方程（不需要特征放缩）
  $\theta=(X^TX)^{-1}X^Ty$，称为设计矩阵（design matrix），需要在第一列加1，对于上面方法也是。该方法不需要选择学习速率也不需要迭代，但是当特征很多数据过大时，运行速度会很慢。

3）代码和结果：

本次练习主要使用了array格式进行计算，先用正规方程求出准确解，再练习梯度下降进行迭代求解。

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

data = np.loadtxt('ex1data1.txt', delimiter=',')
x = data[:, 0]
y = data[:, 1]
m = y.size

#数据可视化
plt.figure(0)
fg1 = plt.scatter(x, y, marker='o', c='b', label='Training data')

'''正规方程法'''
a = np.ones((m, 1)) #将x矩阵第一列赋值为1
x = np.column_stack((a, x)) #矩阵合并
theta = np.linalg.inv(x.T@x)@x.T@y #求矩阵的逆

#增加拟合出的曲线
a = np.linspace(5.0, 22.5, num=5) #等差数列设点，其实可以直接用x
i = 0
b = np.ones(5)
while i<5:
    b[i] = np.array([1,a[i]])@theta.T
    i = i+1
fg2 = plt.plot(a, b, c='r', label='Prediction')
plt.xlabel('Population')
plt.ylabel('Profit')
plt.title('Predicted Profit vs. Population Size')
plt.legend(loc=2)
plt.show

#预测值
x_predict = float(input('请输入预测人口：'))
predict1 = np.array([1,x_predict])@theta.T
print(predict1)

正规方程法最后的假设函数为： $h_\theta(x)=-3.895780884+1.1930336x$
梯度下降法法最后的假设函数为： $h_\theta(x)=-3.89013927+1.19246671x$

注意：在选择学习速率和迭代次数时需要特别小心，学习速率过小导致走不到结果就已经到了迭代次数了，速率过大算法不收敛，尽量多试几个，并且同时调整迭代次数

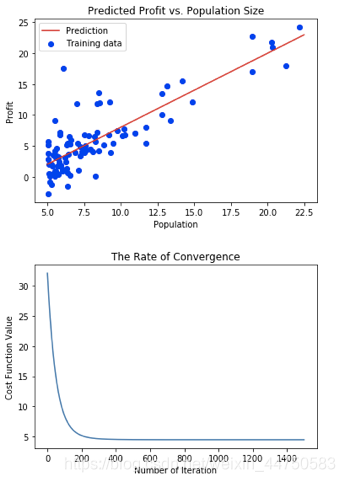
方法对比：

• 梯度下降：需要选择学习率，需要多次迭代，当特征数量n大时也能较好适用，适用于各种类型的模型
• 正规方程：不需要选择学习率，一次计算得出 ，如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为O(n3)，通常来说当n小于10000 时还是可以接受的，但只适用于线性模型，不适合逻辑回归模型等其他模型