吴恩达机器学习作业 线性回归

前言

参考代码与作业指引请自行下载：github链接，以下为答案与解析。

单变量线性回归

首先需要完成对于梯度下降部分算法的代码编写。

1. 最小化代价函数

第一个任务是是完成文件 computeCost.py 中的代码，它是一个计算$J(\theta )$的函数。

根据最小化代价函数的计算公式：
$$J(\theta )=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)}-y^{(i)}{)}^2$$
假设$h_{\theta }(x)$是由线性模型给出的
$$h_{\theta }(x)={\theta }^{T}x={\theta }_0+{\theta }_1{x}_1$$

具体代码实现如下所示：

def computeCost(X, y, theta):
    theta = theta.reshape(1, -1)
    m = X.shape[0]  # 样本数量m
    J = 0
    hx = X @ theta.T
    J = 1/(2*m)*np.sum((hx-y)**2)
    return J

注：python中@代表矩阵做点积操作，A.T代表矩阵A的转置矩阵。

运行主函数，我们可以看到程序运行对于传入不同theta初始值的计算结果均得到了正确结果。说明最小化代价函数代码编写正确。

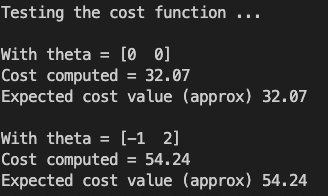
2. 梯度下降

第二个任务是在文件 gradientDescent.py 中实现梯度下降。
根据提供的代码，我需要对于每一轮迭代的实现内容进行补充，并记录每一次迭代过程中的代价变化。
在每次梯度下降中，每次迭代执行更新公式如下：
$${\theta }_j:={\theta }_j-\alpha \frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}$$
具体代码实现如下所示：

def gradientDescent(X, y, theta, alpha, num_iters):
    theta = theta.reshape(1, -1)
    J_history = np.zeros(num_iters)
    m = X.shape[0]

    for i in range(num_iters):
        J_history[i] = computeCost(X, y, theta)
        hx = X @ theta.T
        theta = theta - alpha / m * (X.T @ (hx - y)).reshape(1,-1)
        
    return theta, J_history

运行主函数，我们可以看到程序运行对于theta的迭代计算结果正确。说明梯度下降函数代码编写正确。

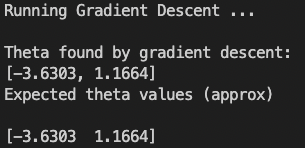
最终可以得到如下的线性回归拟合结果：

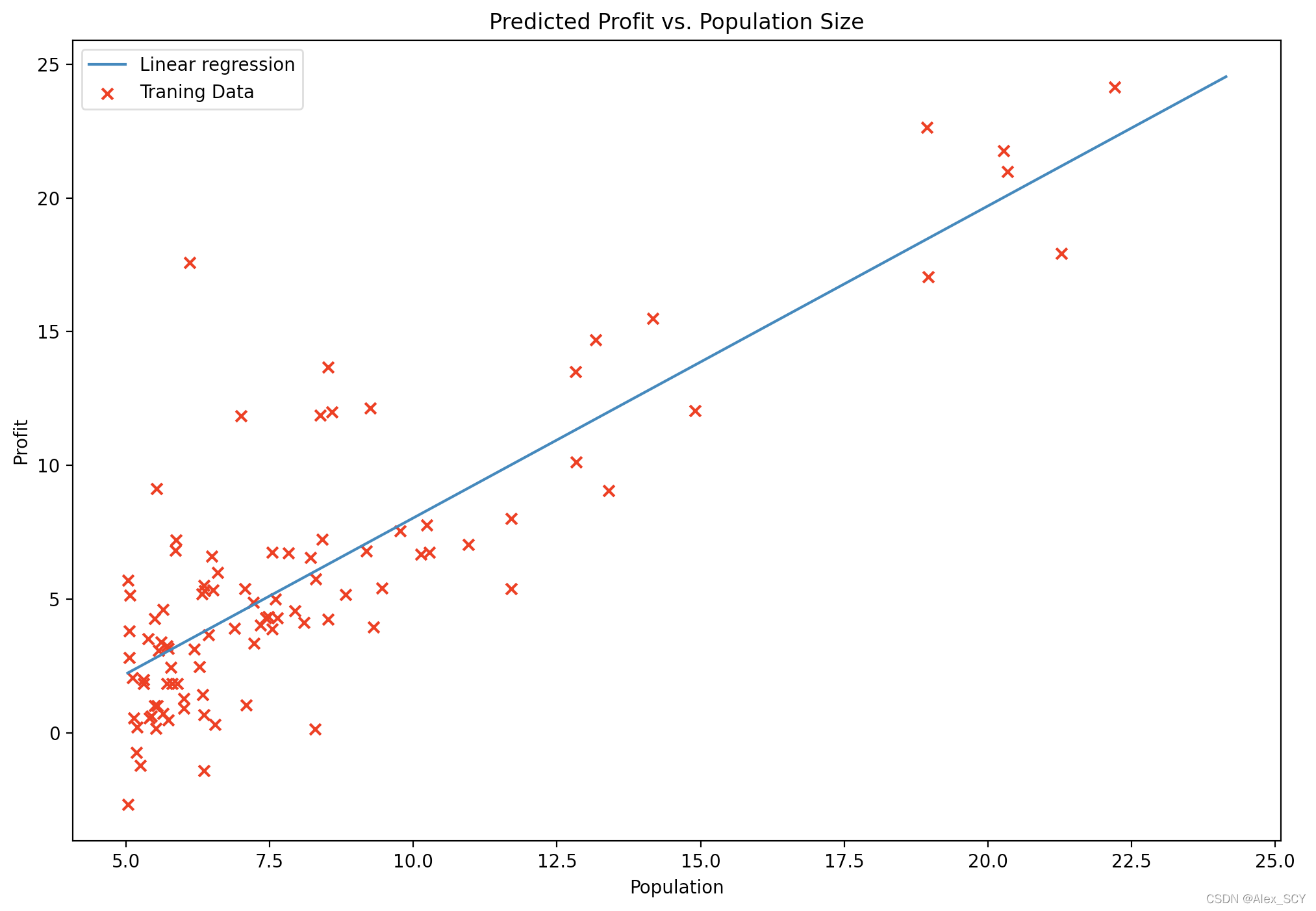
3. 可视化

利用主函数中的meshgrid 和 contourf 命令生成$J(\theta )$的曲面和等高线图
可以看到在红叉处为代价最低点。

多元线性回归

1. 标准化特征

第一个任务是完成 featurennormalize.py 中的代码。
需要完成一下两个任务，首先从数据集中减去每个特征的平均值。然后在减去平均值之后，再将特征值除以它们各自的“标准偏差”。
具体代码实现如下：

def featureNormalize(X):
    X_norm = X
    mu = np.zeros((1, X.shape[1]))
    sigma = np.zeros((1, X.shape[1]))
    
    mu = np.average(X, axis=0)
    sigma = np.std(X, axis=0)
    X_norm = (X - mu) / sigma

    return X_norm, mu, sigma

注：python numpy中需要加入axis=0，即对于矩阵每一列进行求均值或标准差，否则是对于全体数据进行求值。

计算结果：
sigma为[786.2026, 0.7528]， mu为[2000.6808, 3.1702]，与原程序中给出的参考计算结果相同，标准化特征代码编写正确。

2. 梯度下降

第二个任务是完成computeCostMult.py 和 gradientDescentMulti.py 中的代码以实现多变量线性回归的代价函数和梯度下降。
因为第一题的实现方式支持多变量线性回归，因此此阶段不再重述。

def computeCostMulti(X, y, theta):
    theta = theta.reshape(1, -1)
    m = X.shape[0]
    
    J = 0
    hx = X @ theta.T
    J = 1/(2*m)*np.sum((hx-y)**2)
    
    return J

def gradientDescentMulti(X, y, theta, alpha, num_iters):
    theta = theta.reshape(1, -1)
    J_history = np.zeros(num_iters)
    m = X.shape[0]

    for i in range(num_iters):
        J_history[i] = computeCostMulti(X, y, theta)
        hx = X @ theta.T
        theta = theta - alpha / m * (X.T @ (hx - y)).reshape(1,-1)
        
    return theta, J_history

2.1 选择学习速率

在这部分中我尝试了不同的学习速率，并使用提供的函数进行了绘图，结果如下：

学习速率 = 2（迭代次数 = 400）

学习速率 = 0.3（迭代次数 = 50）

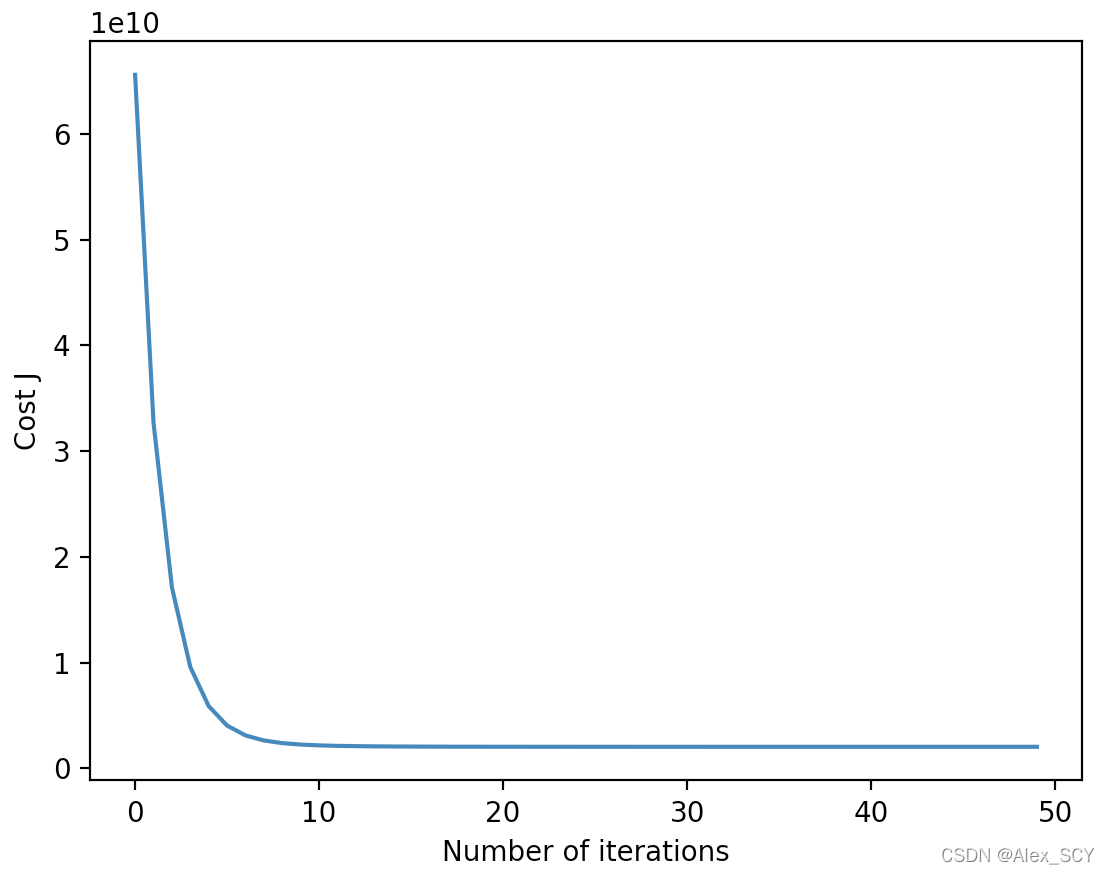
学习速率 = 0.1（迭代次数 = 50）

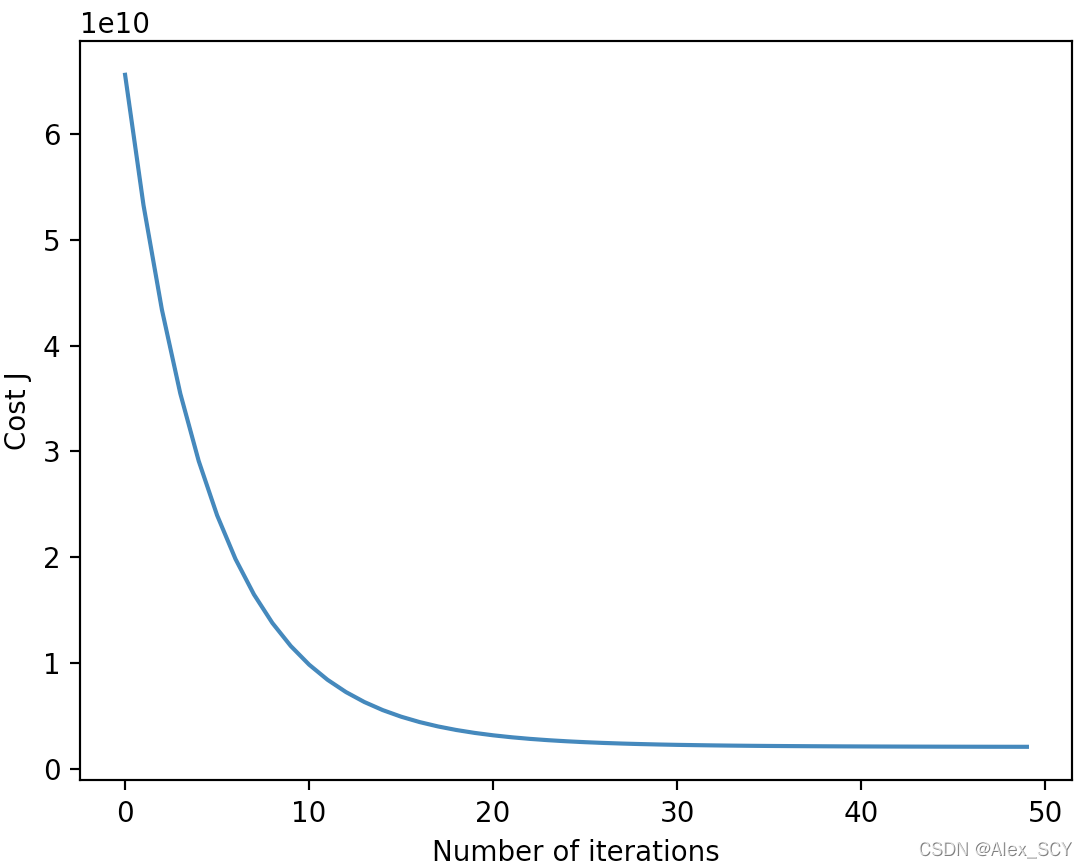
学习速率 = 0.01（迭代次数 = 400）

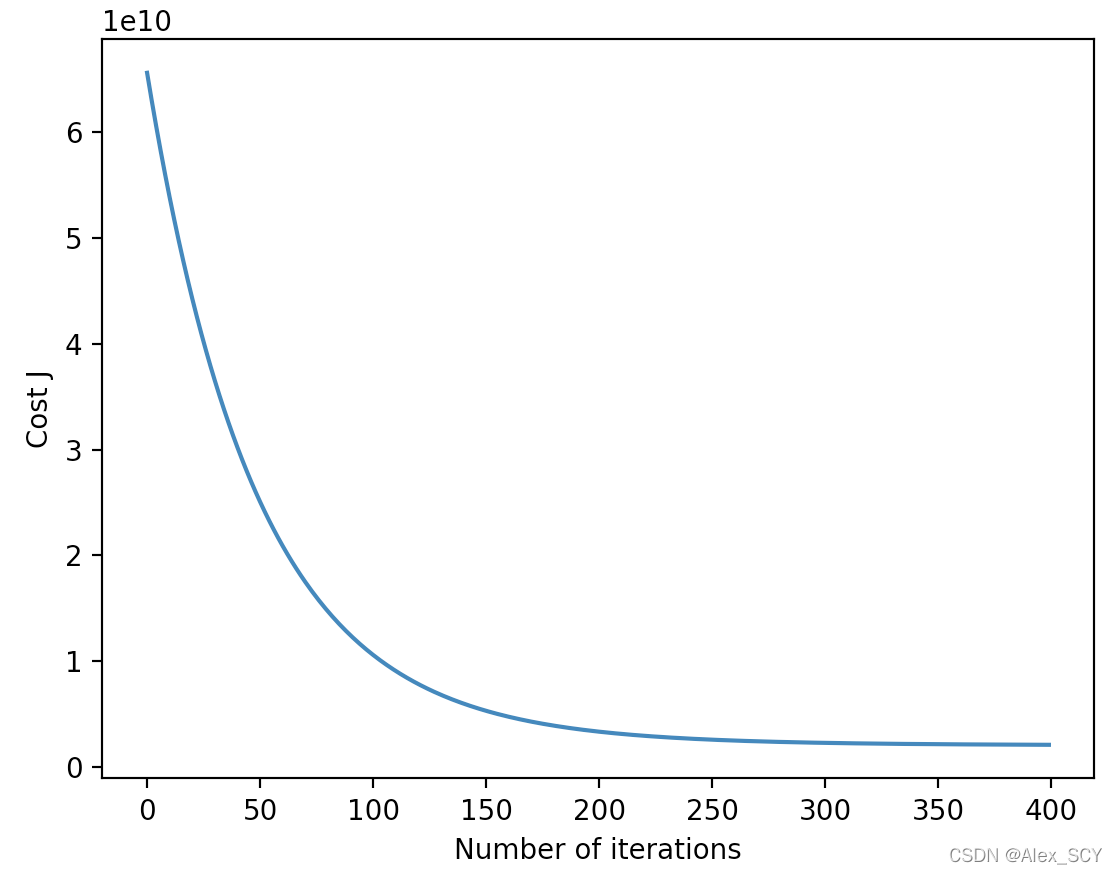
可以看到，当学习速率过大时（$\alpha =2$），反而无法做到降低代价；然后比较了不同的学习速率之间的区别，学习速率越大，迭代次数越少；学习速率越小，迭代次数越多。
当学习速率为0.01，迭代次数为400时，最终得到的theta如下图所示，与原程序提供的参考相同：

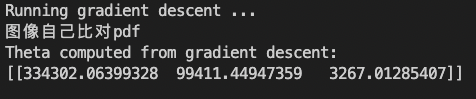
2.2 房价预测

原程序提供了主函数接口，最终预测一个 1650 平方英尺和 3 间卧室的房子的价格为289221.547美元，与参考结果相同。

mydata = (np.array([[1650, 3]]) - mu) / sigma
mydata = mydata.T
mydata = np.insert(mydata, 0, np.ones(1)).reshape(1, -1)
print(mydata)
price = mydata @ theta.T

3.3 正规方程

这三个任务是需要完善 normalEqn.py 中的代码。

def normalEqn(X, y):
    theta = np.zeros((X.shape[1], 1))
    theta = np.linalg.inv(X.T@X)@X.T@y

    return theta

最终得到的theta如下图所示，与原程序提供的参考相同：

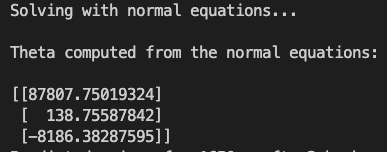
然后在主函数中加入了预测部分：

price = np.array([[1, 1650, 3]]) @ theta

最终利用正规方程预测一个 1650 平方英尺和 3 间卧室的房子的价格为292195.8009美元，与参考结果相同。