单变量线性回归

前言

一、代价函数

1、概念
2、绘制函数

二、梯度下降法

1、梯度
2、公式和学习率
3、多变量函数的梯度下降

三、编程实现

总结

前言

现在我们来学习Machine Learning的第一个算法线性回归（linear regression），废话不多说，先来看看以下这个例子
在这里插入图片描述
上面是上一章节介绍的预测房价的模型，横坐标是Size(feet²)，纵坐标是Price，那么我们怎么根据上面的样本拟合出我们想要的模型（上面品红色的直线）？我们都知道线性方程的公式是这样的f(x) = wx + b，其中的w是斜率，b是截距，那么怎么取得斜率和截距的值呢，这里面就要用到我们的算法—线性回归了。

一、代价函数

1、概念

代价函数（cost function）是用来衡量模型的预测模型与真实数据的偏差，也有别称叫损失函数。有了这个概念，那么就可以选取一个合适的代价函数就可以衡量我们模型的偏差，我们的目的是来最小化（minimize）这个偏差，得到一个相对于模型的最优解即可。线性模型通常采用的是均方误差代价函数，如下示：

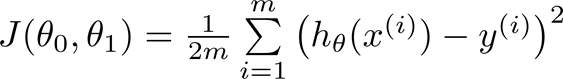
m是数据集中点的个数
½是一个常量，这样是为了在求梯度的时候，二次方乘下来就和这里的½抵消了，自然就没有多余的常数系数，方便后续的计算，同时对结果不会有影响
y 是数据集中每个点的真实y坐标的值
h 是我们的预测函数，根据每一个输入x，根据θ₀，θ₁ 计算得到预测的y值，即
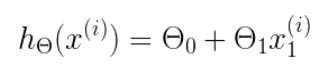
在这里插入图片描述

2、绘制函数

以上的模型我们不妨先看成一个单变量的模型 h(x) = θx，我们假设有这样的样本红色点分别是(1, 1) (2, 2) (3 ,3）那么我们假设
θ = 1时，h(x) = 1x，J(θ) = 1/(2 * 3)[(1 - 1)²+(2 - 2)²+(3 - 3)²] = 0，绘制第一个点下图的浅蓝色 (1, 0)
θ = 0.5时，h(x) = 0.5x，J(θ) = 1/(2 * 3)[(0.5 - 1)²+(0.52 - 2)²+(0.53 - 3)²] ≈ 0.58
················以此类推

在这里插入图片描述
通过上面可以看出代价函数是一个抛物线，最低点是[1, 0]，通过迭代我们就可以得到最优解。以上是单变量的代价函数示意图，那么多个变量的呢，那么就是一个立体的图示了，以下是上面预测房价模型的代价函数示意图
在这里插入图片描述
那么问题来了，2个θ可以用立体图形表示，机器学习中有很多个变量θ，怎么泛化这个模型得到代价函数的最优解呢？有的，那就是大名鼎鼎的梯度下降法

二、梯度下降法

梯度下降（Gradient Descent）是迭代法的一种,可以用于求解最小二乘问题(线性和非线性都可以)。在求解机器学习算法的模型参数，即无约束优化问题时，梯度下降是最常采用的方法之一，另一种常用的方法是最小二乘法。在求解损失函数的最小值时，可以通过梯度下降法来一步步的迭代求解，得到最小化的损失函数和模型参数值。反过来，如果我们需要求解损失函数的最大值，这时就需要用梯度上升法来迭代了。在机器学习中，基于基本的梯度下降法发展了两种梯度下降方法，分别为随机梯度下降法和批量梯度下降法。

这个方法很通用，只要理解了这个方法，无论有多少个变量的模型都可以用这个方法，在此有几个概念要先认识下

1、梯度

梯度实际上就是多变量微分的一般化。也就是函数的偏导数，最直观的理解就是函数在某一点的切线，那么切线是有方向的，沿着梯度下降的方向，就可以一步一步的到达函数的最低点，如下面抛物线。红色的点就是该函数的梯度，不断的迭代就可以不断看见最低点
在这里插入图片描述

2、公式和学习率

梯度下降法的迭代公式如下示
在这里插入图片描述
此公式的意义是：J是关于Θ的一个函数，我们当前所处的位置为Θ0点，要从这个点走到J的最小值点，也就是山底。首先我们先确定前进的方向，也就是梯度的反向，然后走一段距离的步长，也就是α即学习率，走完这个段步长，就到达了Θ1这个点！
通过不断的迭代我们就可以得到Θ的最小值，那么什么时候是最小值呢，我们知道梯度就是切线，当梯度=0时，那么Θ_n = Θ_n-1 - α*0，此时Θ是不会变化的，不必担心随着迭代进行下去会越来越偏差最小值。
α在梯度下降算法中被称作为学习率或者步长，对此要选取一个值，一般我们都是手动取值去0.01的，这里是个学问，不同的模型有不同的学习率选择，是个经验之谈。

3、多变量函数的梯度下降

讲完了梯度，学习率，公式，我们来推倒一下吧，假设我们的公式是这样
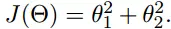
在这里插入图片描述
现在要通过梯度下降法计算这个函数的最小值。我们通过观察就能发现最小值其实就是 (0，0)点。但是接下来，我们会从梯度下降算法开始一步步计算到这个最小值！
我们假设初始的起点为(1， 3）初始的学习率为：0.1
函数的梯度为：
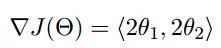
在这里插入图片描述
进行多次迭代：

我们发现，已经基本靠近函数的最小值点

三、编程实现

接下来来实现一个不带变量的梯度下降法

import numpy as np
import matplotlib.pyplot as plt

# 从20-30 取199个点，并把x_data均一化处理转为列向量
x_data_re = np.linspace(0, 30, 200)[:, np.newaxis]
x_data = (x_data_re - x_data_re.min()) / x_data_re.max() - x_data_re.min()
# 取概率分布的均值0，标准差为1的正太分布干扰变量
noise = np.random.normal(0, 0.1, x_data.shape)
# 设图像的斜率是6，生成合成测试数据
w = 6
y_data =x_data*w + noise

# 下面开始用梯度下降法来得到我们的预期值 W
# 目标方程
def h(x_data, w):
    return w*x_data
# 代价函数
def J(x_data, y_data, w):
    return np.mean((h(x_data, w) - y_data)**2)/2
# 代价函数偏导数w
def dJ(x_data, y_data, w):
    return np.mean((h(x_data, w) - y_data)*x_data)
print('初始损失率是 {}'.format(J(x_data, y_data, w)))

# 下面开始进行迭代，lr表示学习率，n_itera表示循环次数，epailon表示当损失函数变化很小时退出的阈值
w_history = list()
def gradient_descent(x_data, y_data, w, lr=1e-3, n_itera = 1e4, epailon = 1e-8):
    W = w
    w_history.append(W)
    itera = 0
    while itera < n_itera:
        # 保存上次的值
        print('此时的w = {}, 循环次数 = {}, 损失值 = {}'.format(W, itera, J(x_data, y_data, W)))
        lastW = W
        # 计算梯度
        gradient_w = dJ(x_data, y_data, W)
        # 梯度下降迭代
        W = W - lr*gradient_w
        # 保存梯度下降的值
        w_history.append(W)
        if abs(J(x_data, y_data, W) - J(x_data, y_data, lastW)) <= epailon:
            print('[退出]此时的w = {}, 循环次数 = {}, 损失值 = {}'.format(W, itera, J(x_data, y_data, W)))
            break
        itera = itera+1

# 假设初始值是W = 0，学习率是0.1
W = 0
gradient_descent(x_data, y_data, W, lr=0.1)

# 画出训练集的点和我们希望的图像
plt.plot(x_data, y_data, 'bo')
plt.plot(x_data, x_data*w_history[-1], 'r-', lw=3)
plt.show()

下面可以看到我们的损失值是不断减低的，W也越来越等于我们的初始设定值6
在这里插入图片描述
下面就是我们原始数据（蓝点）拟合数据（红线）

总结

以上是《吴恩达机器学习》系列视频单变量线性回归。线性回归模型、代价函数和梯度下降法的一些笔记和见解，以便后续学习和查阅。

《吴恩达机器学习》2 单变量线性回归