机器学习笔记(吴恩达)——单变量线性回归

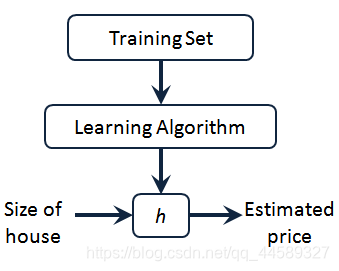
单变量线性回归

符号说明

$m$代表训练集中实例数据
$x$代表输入特征/输入变量
$y$代表目标变量/输出变量
$(x,y)$代表训练集中的实例
$(x_i,y_i)$ 代表第 $i$个观测实例
$h$代表学习算法解决方案或函数

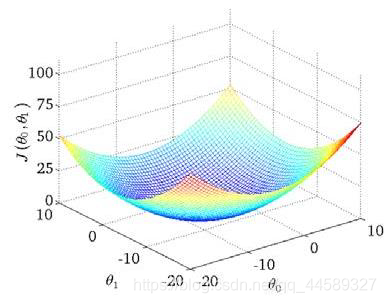
代价函数

代价函数为
$J(\theta_0,\theta_1)=\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)^2$
直观理解如下：要确定出 $\theta_0$, $\theta_1$及使得
$min J(\theta_0,\theta_1)$

梯度下降法

$\theta_{j}:=\theta_{j}-\alpha \frac{\partial}{\partial \theta_{j}} J(\theta)$
对 $\theta$赋值，使得代价函数按照梯度下降最快方向进行，一直迭代下去，其中 $\alpha$为学习率
如果 $\alpha$很小，需要迭代很多步才能到全局最小，如果很大会跳过局部最优导致无法收敛

梯度下降的线性回归

$\frac{\partial}{\partial\theta_j}J(\theta_0,\theta_1)=\frac{\partial}{\partial\theta_j}\frac{1}{2m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)^2$
当 $j=0$时: $\frac{\partial}{\partial \theta_{0}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)$
当 $j=1$时： $\frac{\partial}{\partial \theta_{1}} J\left(\theta_{0}, \theta_{1}\right)=\frac{1}{m} \sum_{i=1}^{m}(\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)x_i)$
因此有如下算法：
$\begin{aligned} &\theta_{0}:=\theta_{0}-a \frac{1}{m} \sum_{i=1}^{m}\left(h_{\theta}\left(x_{i}\right)-y_{i}\right)\\ &\theta_{1}:=\theta_{1}-a \frac{1}{m} \sum_{i=1}^{m}\left(\left(h_{\theta}\left(x_{i}\right)-y_{i}\right) \cdot x_{i}\right) \end{aligned}$
对两个参数 $\theta_0$与 $\theta_1$进行更新，多维空间根据上述公式进行扩展即可。

总结

为什么要用梯度下降法，在进行数据量大的情况下，梯度下降法要比正规方程的方程更加适用