机器学习笔记(吴恩达)——多变量线性回归

多变量线性回归

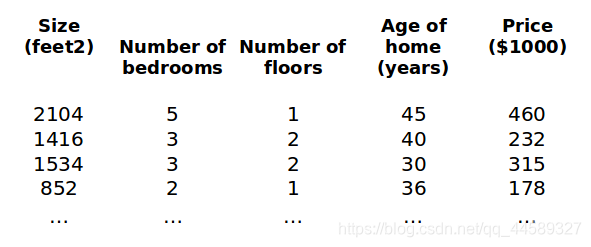
模型的特征为 $(x_1,x_2,...,x_n)$

符号说明

$n$表示特征的数量
$x^{(i)}$代表第 $i$个实例，即特征矩阵中第 $i$行
因此多变量的假设 $h$为：
$h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$
其中 $x_0=1$
此时特征矩阵$X$维度是 $m*(n+1)$,上述公式简化为：
$h_\theta(x)=\theta^TX$

多变量梯度下降

在多变量线性回归中，我们也构建一个代价函数，则这个代价函数是所有建模误差的平方和，即：
$J\left( {\theta_{0}},{\theta_{1}}...{\theta_{n}} \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( h_{\theta} \left({x}^{\left( i \right)} \right)-{y}^{\left( i \right)} \right)}^{2}}}$
针对多变量梯度下降与单变量机理一样，挨个对每个 $\theta$求导
计算代价函数
$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$
其中： ${h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$
引入 $x_0=1$,得到通用的公式如下：
$\theta_{j}:=\theta_{j}-\alpha \frac{1}{m} \sum_{i=1}^{m}\left(\left(h_{\theta}\left(x^{(i)}\right)-y^{(i)}\right) \cdot x_{j}^{(i)}\right)$

特征缩放

最简单的方法：
$x_n=\frac{x_n-u_n}{s_n}$
原始每个值减均值除标准差

学习率

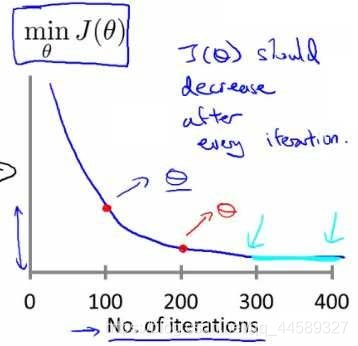
梯度下降算法的每次迭代受到学习率的影响，如果学习率 $a$过小，则达到收敛所需的迭代次数会非常高；如果学习率 $a$过大，每次迭代可能不会减小代价函数，可能会越过局部最小值导致无法收敛。
通常可以考虑尝试些学习率：
$\alpha=0.01，0.03，0.1，0.3，1，3，10$
分别扩大三倍

正规方程

正规方程是通过求解下面的方程来找出使得代价函数最小的参数的：
$\frac{\partial}{\partial{\theta_{j}}}J\left( {\theta_{j}} \right)=0$
假设我们的训练集特征矩阵为 $X$（包含了 ${{x}_{0}}=1$）并且我们的训练集结果为向量 $y$，则利用正规方程解出向量
$\theta ={{\left( {X^T}X \right)}^{-1}}{X^{T}}y$
上标T代表矩阵转置，上标-1 代表矩阵的逆。
设矩阵 $A={X^{T}}X$，则： ${{\left( {X^T}X \right)}^{-1}}={A^{-1}}$
梯度下降与正规方程的比较：

梯度下降	正规方程
需要选择学习率 $\alpha$	不需要
需要多次迭代	一次运算得出
当特征数量 $n$大时也能较好适用	需要计算 ${{\left( {{X}^{T}}X \right)}^{-1}}$ 如果特征数量n较大则运算代价大，因为矩阵逆的计算时间复杂度为 $O\left( {{n}^{3}} \right)$，通常来说当 $n$小于10000 时还是可以接受的
适用于各种类型的模型	只适用于线性模型，不适合逻辑回归模型等其他模型

总结一下，只要特征变量的数目并不大，标准方程是一个很好的计算参数$\theta $的替代方法。具体地说，只要特征变量数量小于一万，我通常使用标准方程法，而不使用梯度下降法。

正规方程不可逆性及公式推导

$\theta=(X^TX)^{-1}X^Ty$
如果 $(X^TX)$不存在逆矩阵，及它是一个奇异矩阵，那么我们要用到伪逆
导致不可逆的原因：
在你想用大量的特征值，尝试实践你的学习算法的时候，可能会导致矩阵 $X'X$的结果是不可逆的。 具体地说，在 $m$小于或等于n的时候，例如，有 $m$等于10个的训练样本也有 $n$等于100的特征数量。要找到适合的 $(n +1)$ 维参数矢量 $\theta$，这将会变成一个101维的矢量，尝试从10个训练样本中找到满足101个参数的值，这工作可能会让你花上一阵子时间，但这并不总是一个好主意。因为，正如我们所看到你只有10个样本，以适应这100或101个参数，数据还是有些少
推导过程：
$J\left( \theta \right)=\frac{1}{2m}\sum\limits_{i=1}^{m}{{{\left( {h_{\theta}}\left( {x^{(i)}} \right)-{y^{(i)}} \right)}^{2}}}$
其中： ${h_{\theta}}\left( x \right)={\theta^{T}}X={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}$
$X$维度是 $m*n$
$\theta$是 $n*1$
$y$是 $m*1$
将向量形式转为矩阵形式如下：
$J(\theta)=\frac{1}{2}(X\theta-y)^T(X\theta-y)\\ =\frac{1}{2}(\theta^TX^T-y^T)(X\theta-y)\\ =\frac{1}{2}(\theta^TXTX\theta-\theta^TX^Ty-y^TX\theta-y^Tyy)$
接下来对 $J(\theta )$偏导，需要用到以下几个矩阵的求导法则:
$\frac{dAB}{dB}={{A}^{T}}$ $\frac{d{{X}^{T}}AX}{dX}=2AX$ $\frac{dX^TA}{dX}=A$
有如下：
$\frac{d(\theta^TXTX\theta)}{d\theta}=2X^TX\theta$ $\frac{d(\theta^TX^Ty)}{d\theta}=X^Ty$
因此
$\frac{\partial J\left( \theta \right)}{\partial \theta }=\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{}({{y}^{T}}X )^{T}-0 \right)\\ =\frac{1}{2}\left(2{{X}^{T}}X\theta -{{X}^{T}}y -{{X}^{T}}y -0 \right)\\ ​={{X}^{T}}X\theta -{{X}^{T}}y$
令
$\frac{\partial J\left( \theta \right)}{\partial \theta }=0$
则有 $\theta ={{\left( {X^{T}}X \right)}^{-1}}{X^{T}}y$