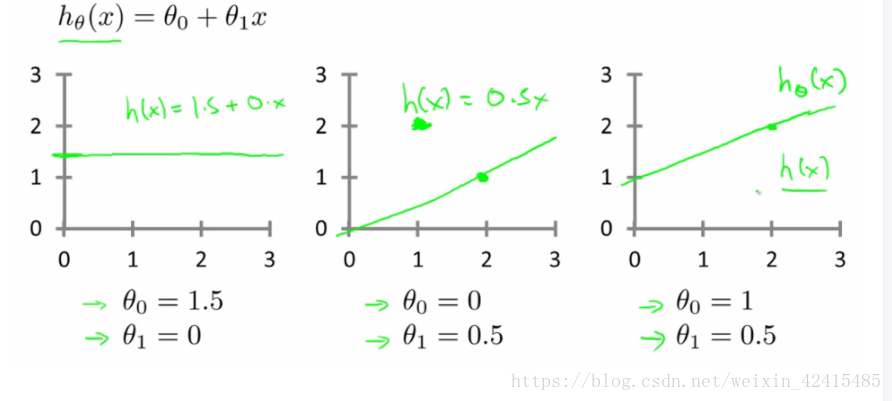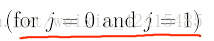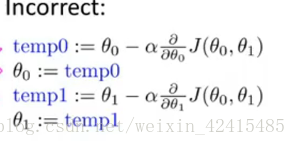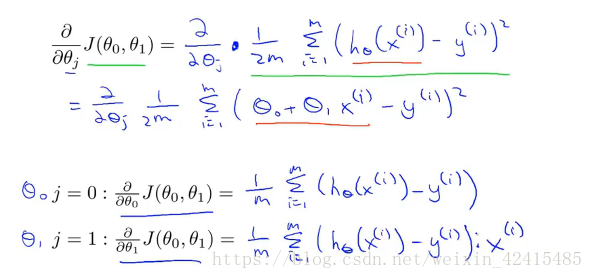-
模型描述:
训练集(training set):是监督学习中独有的概念,由我们人喂给电脑的既有既有特征x又有结果y的数据。下图x是房子面积 ,y是房屋对应的价格
符号记法解释:
(x^(1),y^(1))代表训练集的第一行的数据 x表示输入 y表示输出
监督学习算法的工作流程:
2.假设函数(Hypothesis):
里面有θ0和θ1两个参数,参数的改变将会导致假设函数的变化
数据会以很多点的形式给我们,我们想要解决回归问题,就需要将这些点拟合成一条直线,找到最优的θ0和θ1来使这条直线更能代表所有数据。
举个例子比如说下图所示 一开始我们随意的设θ0=0 θ1=0.5 即y=0.5x 用这条线去拟合我们的数据
发现拟合效果很差 点都不在线上 显然参数还需要进一步优化 那如何优化呢?.
这就需要使用代价函数来求解了
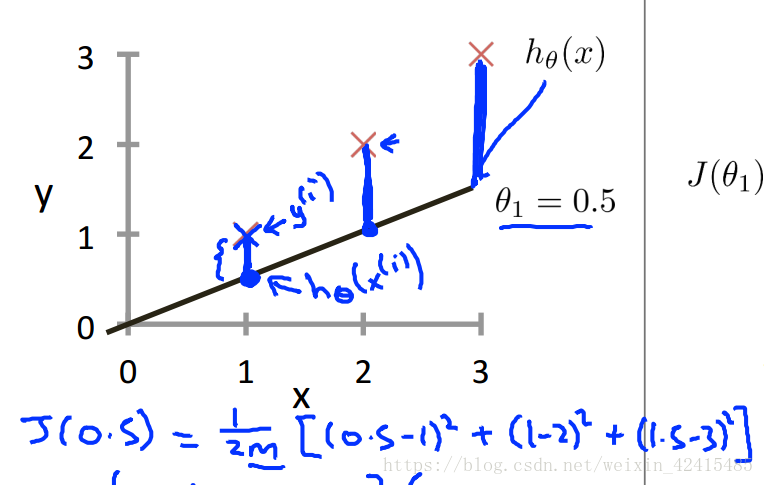
3.代价函数:
代价函数在李航教材也叫损失函数 吴恩达进行了一些区别 初学阶段不用过度的区分:
平方误差代价函数的主要思想就是将实际数据给出的值与我们通过参数θ0 θ1拟合出的线的对应函数值做差然后再平方再求和并除以2m,这样就能求出我们拟合出的直线与实际的差距了。
那么代价函数中为什么分母会有个2m?首先m是训练集的数量 除以m做的其实就是一个取平均,跟期望一个道理,还多了个2是因为后面会对代价函数求导,平方求导会有个2正好与分母抵消方便后续计算。
代价函数用来衡量假设函数的准确性,这个代价函数的值越小就代表模型拟合的越好。
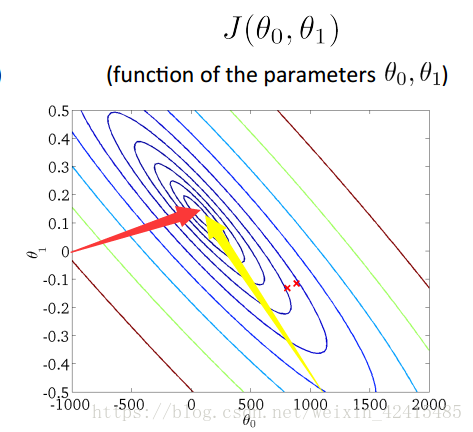
4. 什么叫等高线?
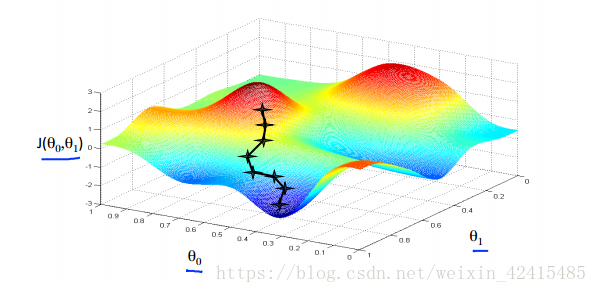
对于一个参数为θ0 θ1的二元函数(下图这是一个任意的假设函数不是代价函数 别弄混)
对上面的图像投影后 由于不同位置陡峭程度不一样 形成一个等高线
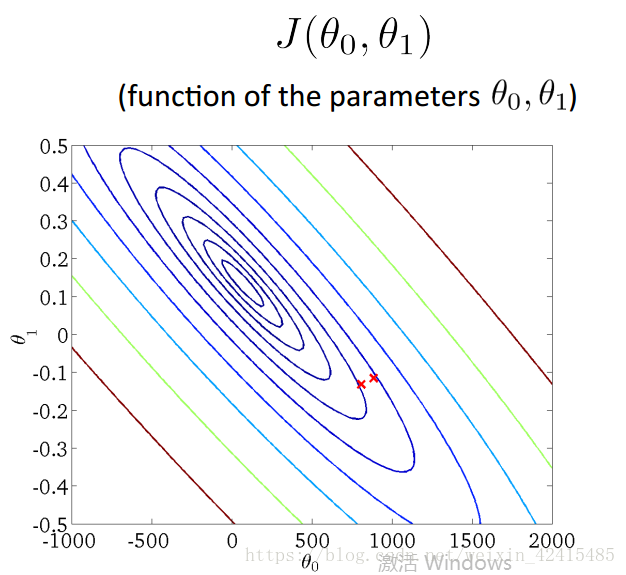
可以看成是一座大山,地面测量大山各点的海拔高度,映射到平面上。高度相同的用线连接起来,形成的这个图就是等高线图
它看着像是一圈圈的大树年轮,越靠近中心海拔越高
中间的圆心 就是损失函数对应值最低的位置 对应3D图的z=j(θ0, θ1)=0
在等高线上每个点的θ0和θ1不同 但是损失值j(θ0, θ1)相同
红色下降到0的速度比黄色下降到0要快 (红比黄更陡)
如红笔:100→50→0 而黄色就是100→90→80……→0
5. 梯度下降法(Gradient Descent):
我们需要用一个算法来使我们的损失函数变小,其中一个方法就是梯度下降法
接下来我就叙述一下梯度下降法:
直观上来形容梯度下降法就是完成一个三部曲:
Step1:先随意初始化一组参数的值 比如说取十字星上面那个红色山顶的尖上作为起点
Step2: 在这个点附近寻找最陡峭的方向 然后朝着这个方向走
Step3:每走一步重复一次step2最直到我们找到全局或者局部最小值
用我们生活中的例子来说就是:把这个算法看成是我们爬山 现在在某个点要下山 每走一步找出当前最佳的下山位置 直到下去(这里简单说一下两个数学概念:
方向导数:函数在某点沿着特点方向上的变化率
梯度:梯度是一个向量 它的方向与最大方向导数的方向一致 它的模是方向导数的最大值 为了加深理解可以看高等数学方向导数与梯度的概念)
不难看出从不同的起点出发会导致不同的局部最优解

我们选一个合适的学习率α然后重复进行这个式子的运算 直到这个偏导数为0 或者说θj不变
使用过程中要注意的是:参数(本例中为两个参数θ0,θ1)要同时更新:
而不是先更新一个再更新另外一个:
α称为学习率(learning rate)永远是一个正数,若α太小,那我梯度移动得就很慢,要很多步才能达到局部最优点;
若α很大,那我可能移动一次直接跳过了局部最优点甚至可能发散
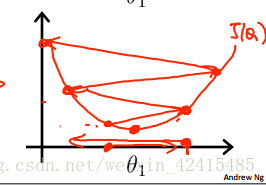
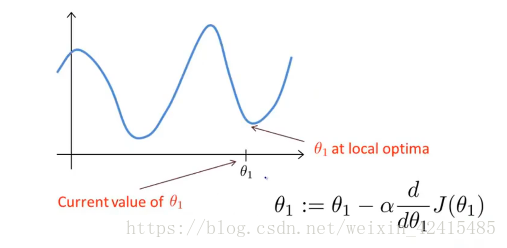
注意我通过梯度下降法得到的局部最低点是和初始值的选择有关的
当θ1的初始点就在局部最优点时 斜率为0 学习就停止了 或者说从另外个初始点开始一直走 走到局部最优点 那我们的学习也停止了
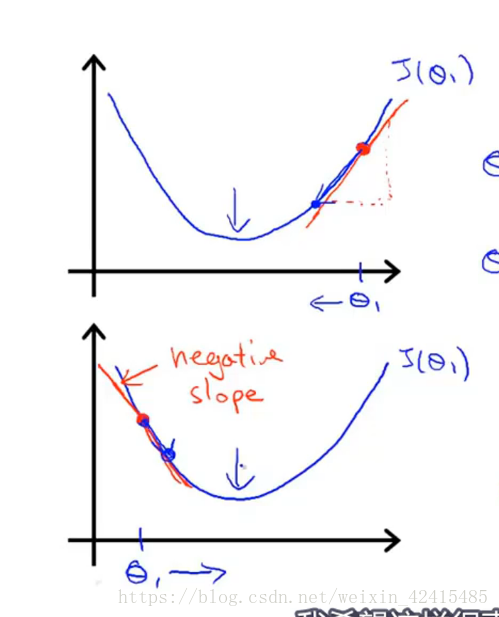
不管初始点是选在左还是右 即:从左到右还是从右到左都是OK的 因为对这个函数左到右的斜率是负 减负就变成正了 故我的θ1越来越往右走 右到左斜率为正 减正越来越往左走 所以不管是哪种这个”爬行的虫子”都会往中间靠
6.梯度下降法应用:
将梯度下降法应用到我们构造的最小化平方差的代价函数当中:
通过计算:不难得出偏导数为:
将偏导数代入式子:(偏导数就是一个函数里有多个变量 某个变量里包含另外一个变量 偏导就是两个变量之间的变化率关系(本人水平有限说不清楚) 知识点请见高等数学多元函数微分学-0-)
(再次强调要同时更新我们的参数)
经过反复更新 我们的参数θ0 θ1都达到最佳值时 我们的代价函数就有了最小值 也即说明我们想用于预测的假设函数最靠谱
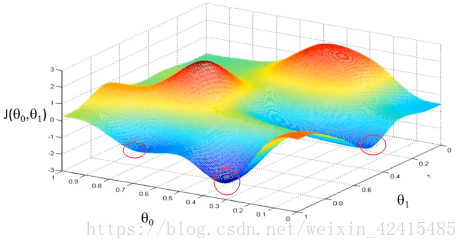
我们应用梯度下降的时候如果遇到这种函数就很可能
陷入红圈所示的局部最优
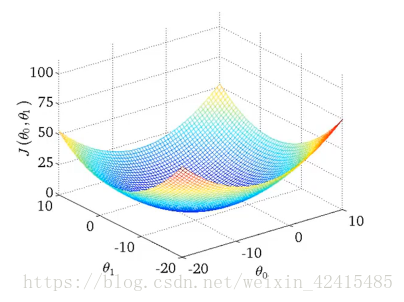
但是通过线性回归得到的代价函数总是一个碗型:
我们称他是一个凸函数(弓形函数或碗型都叫凸函数)
这里他的图形是凹进去的但我们也说他是凸函数
他的极小值就是最小值,他的局部最优解就是全局最优解
凹进去的凸函数:一个函数的图形是凹的的充分条件是函数的二阶导数大于0 凹的定义是对于函数上任意两个点 恒有:两点函数值之和的一半小于两个点之和一半的函数值[f(x1)+f(x2)]/2<f(x1/2+x2/2) (更多数学内容请见高等数学一元函数微分学的凹凸性)
后面会学习一个叫正规方程组的方法(干的活儿和梯度下降一样 但是需要你的线性代数知识) 而梯度下降更适合于数据大的