吴恩达机器学习作业 逻辑回归

前言

参考代码与作业指引请自行下载：github链接，以下为答案与解析。

逻辑回归

1. sigmoid函数

首要需要完成对于sigmoid函数的编写

sigmoid函数的计算公式表达如下：
$$g(z)=\frac{1}{1+e^{-z}}$$

具体代码实现如下所示：

def sigmoid(z):
    g = np.zeros(z.shape)
    g = 1 / (1 + np.exp(-z))
    return g

运行主函数，我们可以看到程序运行对于传入不同值的计算结果均得到了正确结果。说明sigmoid函数代码编写正确。

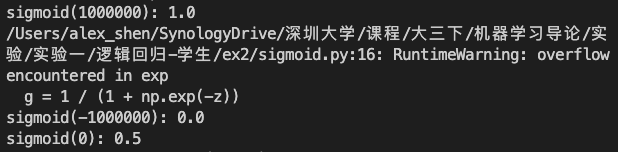
可以看到，当传入的数据为1000000时，因为$e^{1000000}$过大，导致超出计算精度，会报错（但是不会影响最终结果）
因此进行如下优化：

根据传入值是否大于零，进行分类处理，以保证次数始终小于零。

def sigmoid(z):
    g = np.zeros(z.shape)
    func = lambda z: 1 / (1 + np.exp(-z)) if z >=0 else np.exp(z) / (1 + np.exp(z))
    g = func(z)
    
    return g

2. 成本函数和梯度

接下来在 costFunction.py 中完成代码，返回代价和梯度。

逻辑回归的成本函数和梯度的计算公式如下所示：
$$\begin{gathered} J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))] \\ \frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)} \end{gathered}$$

具体代码实现如下所示：

def costFunction(theta, X, y):
    # Initialize
    theta = theta.reshape(1, -1)
    m = X.shape[0]
    J = 0
    grad = np.zeros(theta.shape)
    
    first = -y * np.log(sigmoid(X @ theta.T))
    second = (1 - y) * np.log(1 - sigmoid(X @ theta.T))
    J = np.sum((first - second)) / m
    
    error = sigmoid(X @ theta.T) - y
    for i in range(X.shape[1]):
    	term = error * X[:,i].reshape(-1,1)
	    grad[0][i] = np.sum(term) / m
    
    return J, grad

行主函数，我们可以看到程序运行对于传入不同值的计算结果均得到了正确结果。说明成本函数和代价函数代码编写正确。

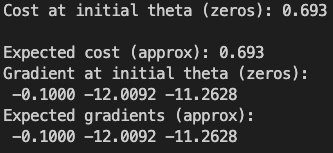
3. 调用fmin_tnc学习参数

运用样例代码，即可获得如下图像，可以正确的进行逻辑回归

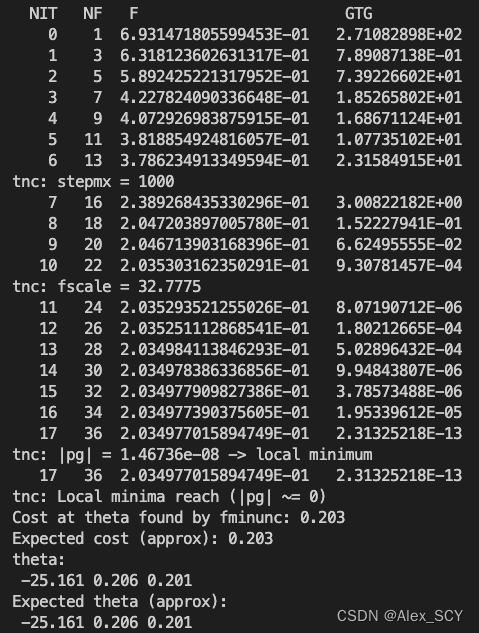
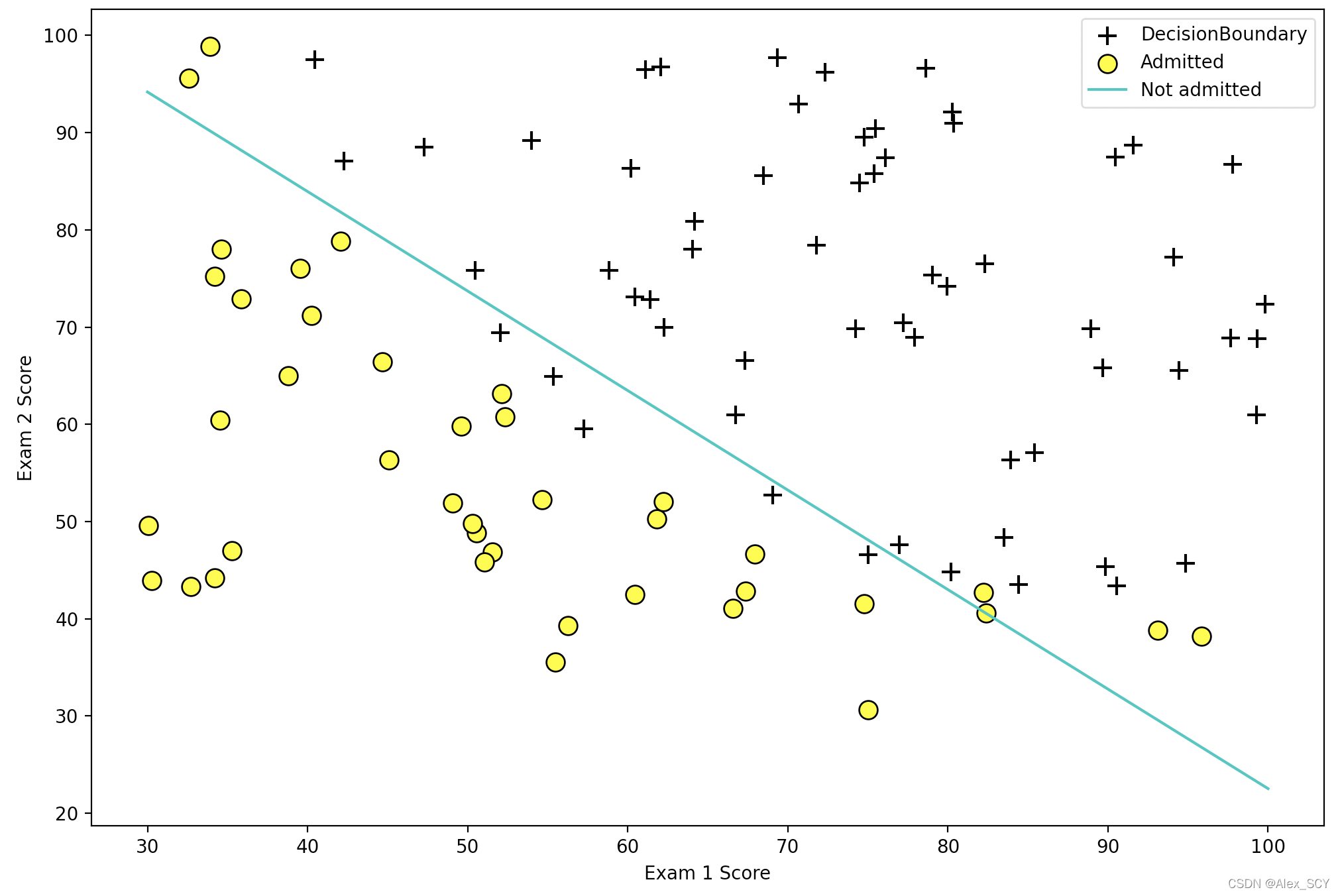
4. logistic回归评估

完善 predict.py 中的代码
根据传入的theta与X，通过sigmoid函数，计算得出属于1的概率。当概率大于0.5时，分类为1；否则分类为0

具体代码实现如下：

def predict(theta, X):
    m = X.shape[0]
    p = np.zeros((m, 1))
    
    possible = sigmoid(X @ theta.T)
    for i in range(m):
        p[i] = 1 if possible[i] >= 0.5 else 0
        
    return p

运行主函数，进行评估，结果如下：

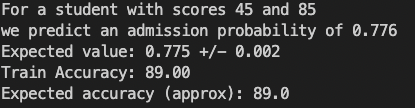
正则逻辑回归

1. 代价函数和梯度

完善 costFunctionReg.py 中的代码计算正则逻辑回归的代价函数和梯度，返回成本和梯度。
其中logistic 回归中的正则化代价函数是：
$$J(\theta )=\frac{1}{m}\sum _{i=1}^m[-y^{(i)}log(h_{\theta }(x^{(i)}))-(1-y^{(i)})log(1-h_{\theta }(x^{(i)}))]+\frac{\lambda }{2m}\sum _{j=2}^n{\theta }_j^2$$

代价函数的梯度是一个向量，其中第 j 个元素定义如下:
$$\begin{gathered} \frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}forj=0 \\ \frac{\partial J(\theta )}{\partial {\theta }_j}=\frac{1}{m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)})x_j^{(i)}+\frac{\lambda }{m}{\theta }_{j}forj\ge 0 \end{gathered}$$

因为公式中的大部分内容与不加入正则化前的公式类似，因此可以调用costFunction中对于代价、梯度的计算结果
具体代码实现如下：

def costFunctionReg(theta, X, y, _lambda):
    theta = theta.reshape(1, -1)
    m = X.shape[0]
    J = 0
    grad = np.zeros(theta.shape)
    
    J = costFunction(theta, X, y)[0] + _lambda / 2 / m * np.sum(theta[:, 1:] ** 2)
    
    for i in range(X.shape[1]):
        if i == 0:
           grad[0][i] = costFunction(theta, X, y)[1][0, 0]
        else:
            grad[0][i] = costFunction(theta, X, y)[1][0, i] + _lambda / m * theta[:, i]

    return J, grad

运行主函数，结果如下：

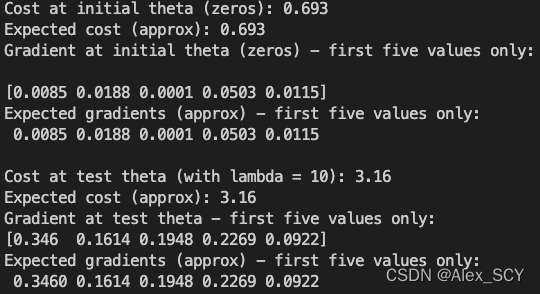
2. 调用fmin_tnc 学习参数

主函数运行结果如下：

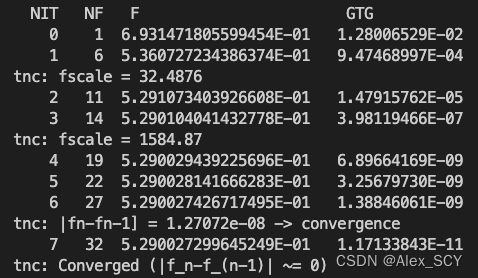
3. 绘制决策边界

调整正则参数lambda，可以绘制出如下不同的决策边界

Train Accuracy: 87.3
Expected accuracy (with lambda = 1): 83.1(approx)
当lambda = 0时，导致过拟合

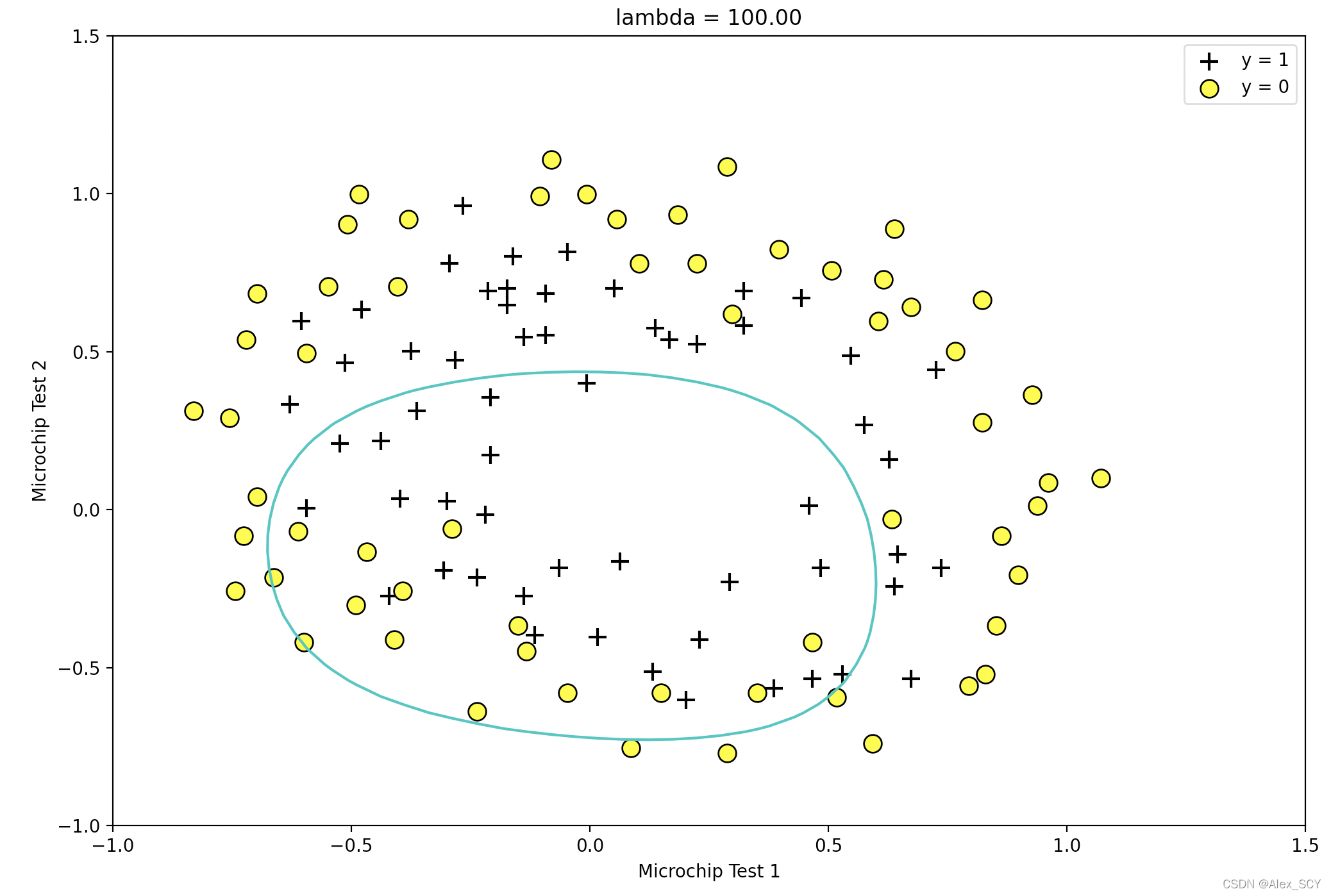
Train Accuracy: 61.0
Expected accuracy (with lambda = 1): 83.1 (approx)
当lambda = 1时，导致欠拟合

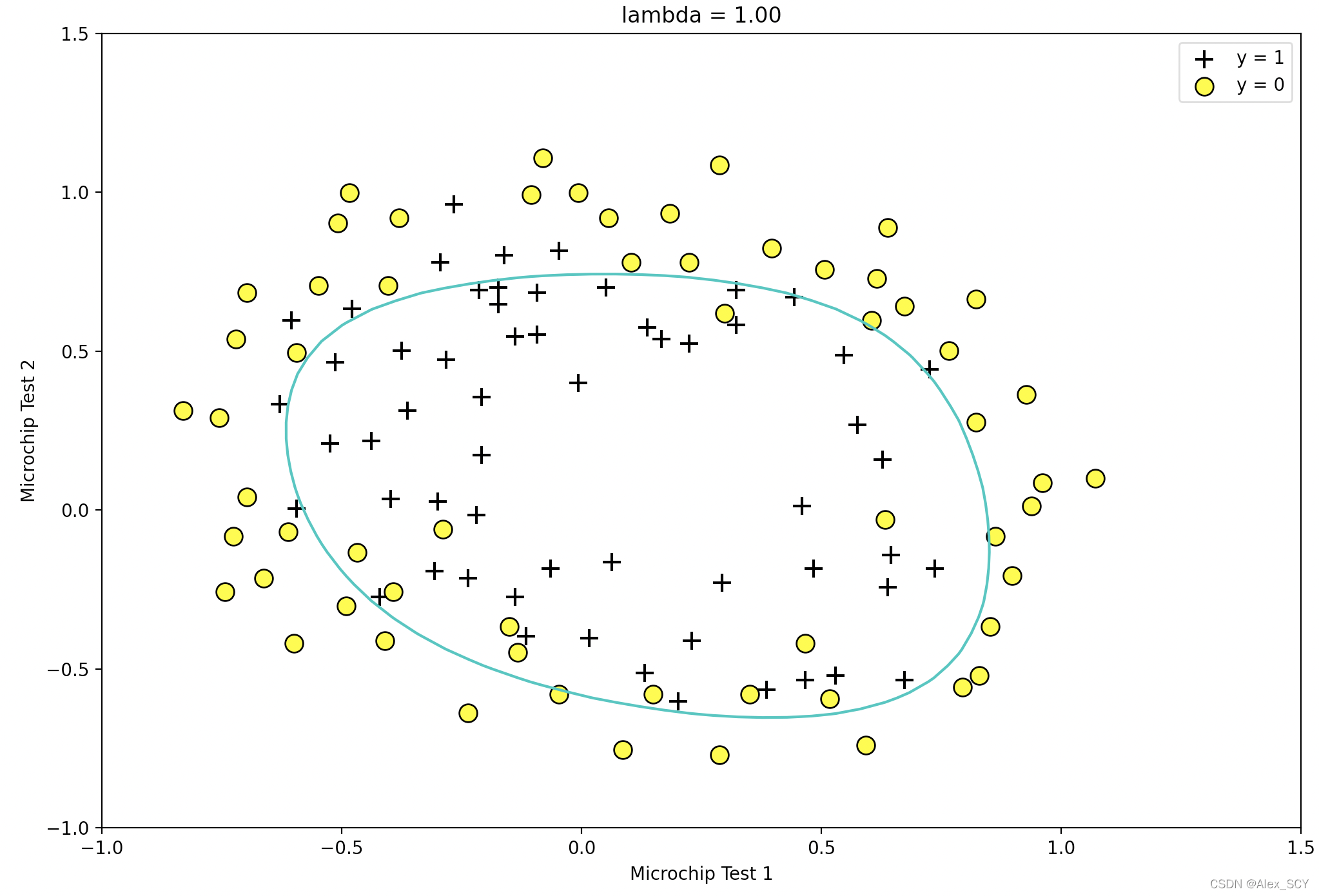
Train Accuracy: 83.1
Expected accuracy (with lambda = 1): 83.1 (approx)
当lambda = 1时，为一个比较合适的参数与决策边界