术语描述：缺乏足够的先验知识，因此难以人工标注类别或进行人工类别标注的成本太高。很自然地，我们希望计算机能代我们完成这些工作，或至少提供一些帮助。根据类别未知(没有被标记)的训练样本解决模式识别中的各种问题，称之为无监督学习。

1.3 泛化能力

是指一个机器学习算法对于没有见过的样本的识别能力

1.4 过拟合欠拟和（方差和偏差以及各自解决办法）、交叉验证

过拟合：当学习器把训练样本自身的一些特点当做了所有潜在样本都会有的一般性质，这样会导致泛化性能下降，这种现象在机器学习中称为过拟合。常见的情况是由于学习能力过于强大，以致于把训练样本所包含的不太一般的特性都学习到了。

欠拟合：与过拟合相对，是指对训练样本的一般性质尚未学好，通常是由于学习能力低下造成的

交叉验证：交叉验证（Cross Validation）是用来验证分类器的性能一种统计分析方法，基本思想是把在某种意义下将原始数据进行分组，一部分做为训练集（training set），另一部分做为验证集（validation set），首先用训练集对分类器进行训练，在利用验证集来测试训练得到的模型（model），以此来做为评价分类器的性能指标。

2、线性回归原理

假设数据集X与y存在线性关系，寻找一条直线，使得样本集X落在该直线上的预测值与真实值y距离最小，得出X数据集的系数，输入新的样本，求出该样本的y值。

3、线性回归损失函数、代价函数、目标函数

损失函数：一个样本的误差

代价函数：所有样本的均值误差

目标函数：所有样本的均方误差

3.1 简单线性回归：

假设找到了最佳拟合的之间方程，y = ax + b，对应每一个样本点 $\LARGE ^{xi}$ ，根据直线方程，预测值为：

希望和的距离尽量小，即：

但是要使得式子可导，转化成平方：

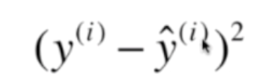
考虑所有的样本，目标变成：

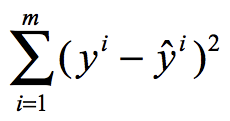
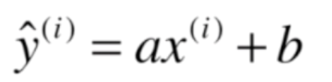
目标：找到a和b，使得下面式子尽可能小，典型的最小二乘法问题，最小化误差的平方

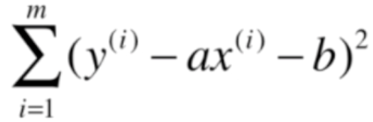
求出a、b值，得到直线方程 y = ax + b，将未知的x值带入方程，求得y值。

3.2 多元线性回归--多个特征值的线性回归

目标使得尽可能小，，找到 $\LARGE \theta _{0}$ ,..... $\LARGE \theta _{n}$ ，使得该式子尽可能小，

缺点：时间复杂度高

优点：不需要对数据做归一化处理

4、优化方法（梯度下降法、牛顿法、拟牛顿法等）

样本特征数量多的情况下，多元线性正规方程解耗时长，梯度下降法可以解决这个问题。

4.1 梯度下降法

个人通俗理解：目标函数是凸函数时，沿着函数最快的下降方向，找到局部的最优解。

假设目标函数是：J = ( $\large \theta$ )，设置初始的 $\large \theta$ 值，通过对 $\large \theta$ 求导，找到函数最快下降的方向，每次下降步长，其中设置成0.01，经过搜索迭代后，直到函数值变化很小，就停止搜索，找到了局部最优解。

注意事项：

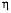也称为学习速率，设置过小，每次移动的步长很小，导致搜索过程过慢，需要增加搜索次数，耗时过长，设置过大，函数下降的方法可能不会沿着最小方向下降，导致不收敛。
梯度下降法，样本量大时，耗时长，可以选择随机梯度下降法或者小批量随机梯度下降法。

4.2 牛顿法：这个迭代过程先随机先一个初始点x0x0，过(x0x0,f(x0x0))做函数的切线，将切线和横坐标的切点做下一个点继续做切线，知道切线和函数的切点落在横坐标上。

4.3 拟牛顿法：没看懂

5、线性回归的评估指标

5.1 均方误差，衡量真实值与预测值平方的均值误差，MAE越小，拟合效果越好，缺点在于做了平方，与真实值的量纲不一致，难以直观看出差距，于是提出RMSE：

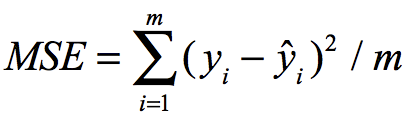
5.2 均方跟误差RMSE，可以解决量纲不一致的问题。

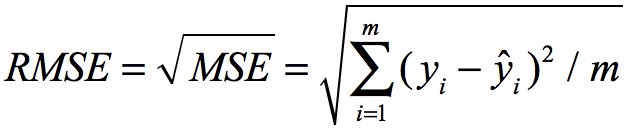
5.3 MAE 平均绝对误差，Mean Absolute Error

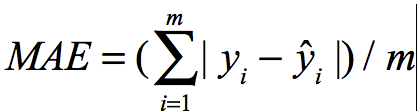
5.4 但是在不同的场景下，不能直接比较算法的性能，不能判断算法是在哪种场景下更合适。

R^2就解决了这类问题，转化了[0,1]之间判断，不同场景下可以比较算法的性能。

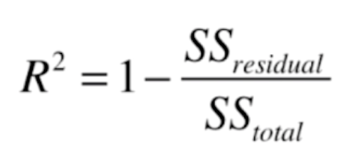
6、sklearn 参数详解

这里自己实现回归算法，运用正规方程解、梯度下降优化方法，也是熟悉参数的过程。

# 回归算法
# 1、正规方程训练参数，可以不做数据归一化
# 2、梯度下降法训练参数，需要做数据归一化，因为放到真是环境中，特征的维度不同，有的数值非常大，会造成下降步长大，导致不收敛，
#    数值太小，导致下降步长小，训练的次数有限，找不到函数的最小值
# 3、一般梯度下降法的，梯度计算函数，可以转换成向量化计算，在特征值多的情况下，可以减少计算的时间，但是样本量大的情况下，时间优势不明显。
# 4、基于3的算法，是批量梯度下降法，每次梯度搜索，所有的样本都会参与，于是产生了随机梯度下降法。

import numpy as np

class LinearRegression():

    def __init__(self):
        self.intercept__ = None
        self.coefficinents__ = None
        self.__theta = None

    def fit_normal(self, X_train, y_train):
        assert X_train.shape[0] == y_train.shape[0]
        # a = np.ones(shape=(X_train.shape[0],1), dtype=float)
        # print(a.shape)
        # print(X_train.shape)
        X_b = np.hstack([np.ones(shape=(X_train.shape[0],1), dtype=float), X_train])
        self.__theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train)
        self.intercept__ = self.__theta[0]
        self.coefficinents__ = self.__theta[1:]

        return self

    # 梯度下降法
    def fit_gd(self, X_train, y_train):
        def j(X, y, theta):
            X_b = np.hstack([np.ones(shape=(len(X), 1), dtype=float), X])
            j_value = np.sum((y - X_b.dot(theta)) ** 2) / len(X)
            return j_value

        # 损失函数的梯度
        def dj(X, y, theta):
            X_b = np.hstack([np.ones(shape=(len(X), 1), dtype=float), X])
            res = np.empty(len(theta))
            res[0] = np.sum(X_b.dot(theta) - y)
            for i in range(1, len(theta)):
                res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            return res * 2 / len(X_b)

        def LinearGrandientDesecent(X, y, initial_theta, eta=0.01, esilon=1e-8, cnt=100000000):
            theta = initial_theta
            cnt_ = 0
            while cnt_ < cnt:
                dj_theta = dj(X, y, theta)
                last_theta = theta
                theta = last_theta - eta * dj_theta

                if abs(j(X, y, last_theta) - j(X, y, theta)) < esilon:
                    break
            cnt_ += 1
            return theta

        initial_theta = np.zeros(X_train.shape[1] + 1)  # theta
        theta = LinearGrandientDesecent(X_train, y_train, initial_theta)
        self.__theta = theta
        self.intercept__ = theta[0]
        self.coefficinents__ = theta[1:]
        return self

    # 梯度下降法，向量化计算梯度
    def fit_vgd(self, X_train, y_train):
        def j(X, y, theta):
            X_b = np.hstack([np.ones(shape=(len(X), 1), dtype=float), X])
            j_value = np.sum((y - X_b.dot(theta)) ** 2) / len(X)
            return j_value

        # 损失函数的梯度
        def dj(X, y, theta):
            X_b = np.hstack([np.ones(shape=(len(X), 1), dtype=float), X])
            # res = np.empty(len(theta))
            # res[0] = np.sum(X_b.dot(theta) - y)
            # for i in range(1, len(theta)):
            #     res[i] = (X_b.dot(theta) - y).dot(X_b[:, i])
            return X.T.dot(X_b - y) * 2 / len(X_b)

        def LinearGrandientDesecent(X, y, initial_theta, eta=0.01, esilon=1e-8, cnt=100000000):
            theta = initial_theta
            cnt_ = 0
            while cnt_ < cnt:
                dj_theta = dj(X, y, theta)
                last_theta = theta
                theta = last_theta - eta * dj_theta

                if abs(j(X, y, last_theta) - j(X, y, theta)) < esilon:
                    break
            cnt_ += 1
            return theta

        initial_theta = np.zeros(X_train.shape[1] + 1)  # theta
        theta = LinearGrandientDesecent(X_train, y_train, initial_theta)
        self.__theta = theta
        self.intercept__ = theta[0]
        self.coefficinents__ = theta[1:]
        return self


    def predict(self, X_test):
        assert X_test.shape[1] == self.coefficinents__.shape[0]
        assert self.__theta is not None
        X_test_b = np.hstack([np.ones(shape=(X_test.shape[0],1), dtype=float), X_test])
        y_predict = X_test_b.dot(self.__theta)

        return y_predict

    def score(self, X_test, y_test):
        assert X_test.shape[0] == y_test.shape[0]
        y_predict = self.predict(X_test)
        r2_squerd =1 - (y_test - y_predict).dot(y_test - y_predict)/(np.mean(y_test) - y_test).dot(np.mean(y_test) - y_test)
        return r2_squerd

初级算法梳理--线性回归

目录

猜你喜欢