Datawhale-初级算法梳理-Day1-线性回归算法梳理

1.机器学习的一些概念

a) 监督学习

监督学习是机器学习的一种方法，可以由训练资料中学到或建立一个模式，并依此模式推测新的实例。训练资料是由输入物件（通常是向量）和预期输出所组成。函数的输出可以是一个连续的值（称为回归分析），或是预测一个分类标签（称作分类）。

b) 无监督学习

相对于监督学习，无监督学习没有给定事先标记过的训练示例，自动对输入的数据进行分类或分群。

c) 泛化能力

泛化能力通俗来讲就是指学习到的模型对未知数据的预测能力。我们通常通过测试误差来评价学习方法的泛化能力。

d) 过拟合和欠拟合

• 过拟合
  当学习器把训练样本学得“太好”了的时候，很可能已经把训练样本自身的一些特点当作了所有潜在样本都会具有的一般性质性质，这样就会导致泛化性能下降。这种现象在机器学习中称为“过拟合”。过拟合时方差较高。
  解决办法：

1. 获取更多数据
   这是解决过拟合最有效的方法，只要给足够多的数据，让模型「看见」尽可能多的「例外情况」，它就会不断修正自己，从而得到更好的结果。
2. 正则化
   正则化是指约束模型的学习以减少过拟合的过程。如L1和L2正则化，正则化的一个最强大的特性就是能向损失函数增加“惩罚项”。所谓『惩罚』是指对损失函数中的某些参数做一些限制。最常见的惩罚项是L1和L2：
   L1惩罚项的目的是将权重的绝对值最小化
   L2惩罚项的目的是将权重的平方值最小化
   

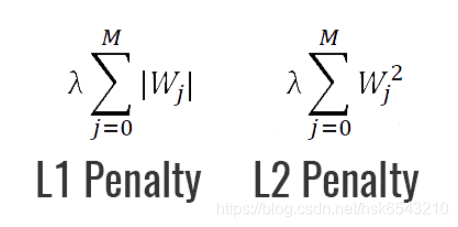
• 欠拟合
  指的是对训练样本的一般性质尚未学好。欠拟合时偏差较高。
  解决办法：

1. 添加其他特征项，有时候我们模型出现欠拟合的时候是因为特征项不够导致的，可以添加其他特征项来很好地解决。例如，“组合”、“泛化”、“相关性”三类特征是特征添加的重要手段，无论在什么场景，都可以照葫芦画瓢，总会得到意想不到的效果。除上面的特征之外，“上下文特征”、“平台特征”等等，都可以作为特征添加的首选项。
2. 添加多项式特征，这个在机器学习算法里面用的很普遍，例如将线性模型通过添加二次项或者三次项使模型泛化能力更强。例如上面的图片的例子。
3. 减少正则化参数，正则化的目的是用来防止过拟合的，但是现在模型出现了欠拟合，则需要减少正则化参数。

过拟合和欠拟合的直观类比：

e) 交叉验证

“交叉验证法"先将数据集D划分为k个大小相似的互斥子集，即D₁ U D₂ U…U D_k, D_i n D_j = ø ( í != j).每个子集D_i都尽可能保持数据分布的一致性，即从D中通过分层采样得到.然后，每次用k-1个子集的并集作为训练集,余下的那个子集作为测试集;这样就可获得k组训练/测试集，从而可进行k次训练和测试,最终返回的是这k个测试结果的均值。显然，交叉验证法评估结果的稳定性和保真性在很大程度上取决于k的取值，为强调这一点，通常把交叉验证法称为"k折交叉验证”.k最常用的取值是10，此时称为10折交叉验证;其他常用的k有5、20等。

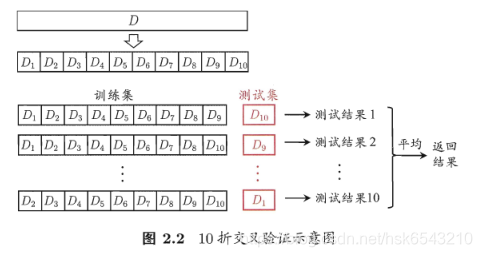
为减小因样本划分不同而引入的差别，k折交叉验证通常要随机使用不同的划分重复p次，最终的评估结果是这p次k折交叉验证结果的均值，例如常见的有" 10次10折交叉验证”。

2.线性回归的原理

线性回归是一种通过属性的线性组合来进行预测的线性模型，其目的是找到一条直线或者一个平面或者更高维的超平面，使得预测值与真实值之间的误差最小化。模型通式为：
${f(x_i)=wx_i+b}$
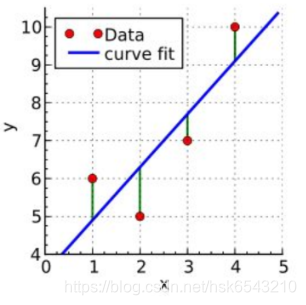
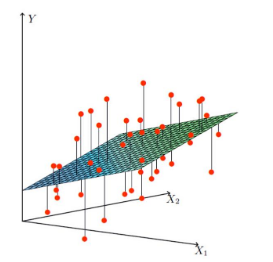
以下分别是一元和二元变量的线性回归实例图：

3.线性回归损失函数、代价函数、目标函数

• 损失函数：模型在单个样本上的误差
  ${|h_\theta(x^{(i)})-y^{(i)})|}$
• 代价函数：所有样本误差的平均值
  ${J(\theta)=\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2}$
• 目标函数：代价函数加入了正则惩罚项后得到的最终优化函数
  ${\frac{1}{2m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^n{\theta_j}^2}$

4.优化方法

a) 梯度下降法

梯度下降法是一种迭代算法．选取适当的初值 ${x^{(0)}}$，不断迭代，更新x的值，
进行目标函数的极小化，直到收敛．由于负梯度方向是使函数值下降最快的方向，
在迭代的每一步，以负梯度方向更新x的值，从而达到减少函数值的目的。

假设 ${f(x)}$是 ${R^n}$上具有一阶连续偏导数的函数．要求解的无约束最优化问
题是
${min \atop x\in{R^n} }f(x)$

由于 ${f(x)}$具有一阶连续偏导数，若第k次迭代值为 ${x^{(k)}}$，则可将 ${f(x)}$在 ${x^{(k)}}$附近进行一阶泰勒展开：
${f(x)=f(x^{(k)})+g^T_k(x-x^{(k)})}$

这里， ${g_k=g(x^{(k)})=\nabla f(x^{(k)})}$ 为 ${f(x)}$在 ${x^{(k)}}$的梯度。
求出第k+1次迭代值 ${x^{(k)}}$：
${x^{(k+1)}}\leftarrow x^{(k)}+\lambda_kp_k$

其中， ${p_k}$是搜索方向，取负梯度方向 ${p_k=-\nabla f(x^{(k)})}$， ${\lambda_k}$是步长，由一维搜索确定，即 ${\lambda_k}$使得
${f(x^{(k)}+\lambda_kp_k)={min \atop \lambda \ge0 }f(x^{(k)}+\lambda p_k)}$

b) 牛顿法

牛顿法和拟牛顿法也是求解无约束最优化问题的常用方法，有收敛速度快的优点．牛顿法是迭代算法，每一步需要求解目标函数的海赛矩阵的逆矩阵，计算比较复杂。

c) 拟牛顿法

拟牛顿法通过正定矩阵近似海赛矩阵的逆矩阵或海赛矩阵，简化了牛顿法复杂的计算过程。

5.线性回归的评价指标

• MAE(Mean Absolute Error) 平均绝对误差
  ${MAE=\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})}$
• MSE(Mean Square Error) 平均平方差/均方误差是回归任务最常用的性能度量。
  ${MSE=\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2}$
• RMSE(Root Mean Square Error) 方均根差
  ${RMSE=\sqrt{\frac{1}{m}\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2}}$
  更多参考这里

6.sklearn参数详解

参考(sklearn)逻辑回归linear_model.LogisticRegression用法