机器学习算法-线性回归
一、相关理论基础
1.1 凸函数
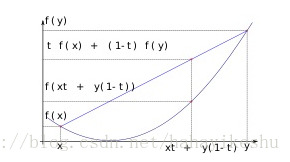
某个向量空间的凸子集(区间)上的实值函数,如果在其定义域上的任意两点 ,有 f(tx + (1-t)y) <= tf(x) + (1-t)f(y),则称其为该区间上的凸函数;
1.2 线性
线性并不等于直线。线性函数的定义是:一阶(或更低阶)多项式,或零多项式。当线性函数只有一个自变量时,y = f(x);
如果有多个独立自变量,表示为:
总结: 特征是一维的,线性模型在二维空间构成一条直线;特征是二维的,线性模型在三维空间中构成一个平面;若特征是三维的,则最终模型在四维空间中构成一个体;以此类推……
1.3 极大似然估计
定义:从样本中随机抽取n个样本,而模型的参数估计量使得抽取的这n个样本的观测值的概率最大。最大似然估计是一个统计方法,它用来求一个样本集的概率密度函数的参数。
二、线性回归
定义:
回归在数学上来说是给定一个点集,就能够用一条曲线去拟合之。如果这个曲线是一条直线(超平面),那就被称为线性回归。若不是一条直线则称为非线性回归,常见有多项式回归、逻辑回归等。
线性模型优劣:
优点:结果易于理解,计算上不复杂;
缺点:对非线性的数据拟合不好;
2.1 线性回归模型
一般线性模型表示:
其中,
等表示不同的特征,
,
等表示权重;用向量的形式表示为:
。
2.2 最小二乘法
最小二乘法是基于均方误差最小化来进行模型求解的方法,最小二乘法试图找到一条直线,使所有的样本到直线上的欧式距离之和最小。
线性模型用一个直线(平面)拟合数据点,找出一个最好的直线(平面)即要求每个真实点距离平面的距离最近。即使得残差平方和(Residual Sum of Squares, RSS)最小:
另一种情况下,为消除样本量的差异,也会用最小化均方误差(MSE)拟合:
2.3 极大似然法
真实值与预测值存在的差异(用
表示误差):
并且误差是独立并且同分布的,并且服从均值为0 的方差为
的高斯分布:
将误差带入以上公式:
对已发生的样本,出现的概率为:
两边取对数:
使出现的概率最大,即使上面的方程达到最大,通过简单变换转换成求最小值问题,得使以下方程最小:
以上方程跟最小二乘法相似,以下均以此函数作为损失函数。
三 求解
3.1 求解-正规方程法
因此知道特征矩阵以及标签就可以求出相应的权重。
3.2 求解-梯度下降
梯度下降法基于的思想为:要找到某函数的极小值,则沿着该函数的梯度方向寻找。若函数为凸函数且约束为凸集,则找到的极小值点则为最小值点。
梯度下降基本算法为: 首先用随机值填充θ(这被称为随机初始化),然后逐渐改进,每次步进一步(步长α),每一步都试图降低代价函数,直到算法收敛到最小。
求解梯度常见有以下几个方法:
批量梯度下降(Batch Gradient Descent,BGD)
批量梯度下降法,是梯度下降法最常用的形式,具体做法也就是在更新参数时使用所有的样本来进行更新。
优点:得到全局最优解;易于并行实现
缺点:当样本数目很多时,训练过程会很慢
随机梯度下降(Stochastic Gradient Descent)
随机梯度下降法,其实和批量梯度下降法原理类似,区别在与求梯度时没有用所有的m个样本的数据,而是仅仅选取一个样本j来求梯度。对应的更新公式是:
优点:训练速度快
缺点:准确度下降,可能跳出最优解,不是全局最优
小批量梯度下降法(Mini-batch Gradient Descent)
进行迭代时选用部分样本, 1<x < m
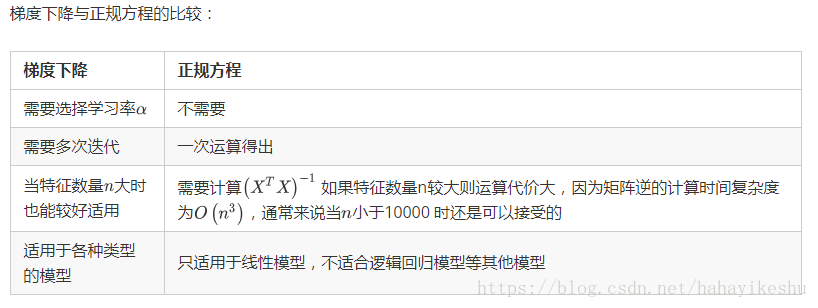
3.3 梯度下降方法与正规方程比较
四 模型评估
回归评价指标 MSE(均方误差)、RMSE(均方根误差)、MAE(平均绝对误差)、R-Squared;Sklearn 中使用R-squared
五 sklearn实现
六 关于L1和L2的直观理解
七 参考链接
https://blog.csdn.net/hahayikeshu/article/details/82964574
https://note.youdao.com/share/?id=981825c617d47c10f4e0c373e8b7bfff&type=note#/